рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Элементы линейной алгебры и аналитической геометрии
Реферат Курсовая Конспект
Элементы линейной алгебры и аналитической геометрии
Элементы линейной алгебры и аналитической геометрии - раздел Философия, Министерство Образования И Науки Российской Федерации ...
Министерство образования и науки Российской Федерации
Волжский институт строительства и технологий
(филиал) государственного образовательного учреждения
высшего профессионального образования
«Волгоградский государственный архитектурно-строительный университет»
Кафедра высшей математики
Элементы линейной алгебры и
Аналитической геометрии
Методические указания по самостоятельной работе и
Задания контрольной работы
Для студентов заочной формы обучения
по направлениям «Строительство» и
«Наземные транспортно-технологические комплексы»
Волжский, 2012
УДК 65в631
Элементы линейной алгебры и аналитической геометрии: методические указания по самостоятельной работе и задания контрольной работы для студентов заочной формы обучения по направлениям «Строительство» и «Наземные транспортно-технологические комплексы» / ВИСТех (филиал) ВолгГАСУ ; [сост. Е. В. Абрамов, Д. П. Торшин]. – Волжский : ВИСТех (филиал) ВолгГАСУ, 2012. – 46 с.
Представлен необходимый теоретический материал и варианты контрольной работы по теме «Элементы линейной алгебры и аналитической геометрии» с примером ее выполнения, а также требования к оформлению контрольных работ, вопросы для самопроверки и список рекомендуемой литературы.
Предназначено для студентов, обучающихся в 1 семестре на заочной форме обучения по направлениям «Строительство» и «Наземные транспортно-технологические комплексы».
Библиогр. 4 Табл. 1 Ил. 13
Содержание
| 1. Методические указания по самостоятельной работе……………… | |
| 2. Требования к оформлению контрольной работы………………….. | |
| 3. Рекомендуемая литература для самостоятельной работы………… | |
| 4. Контрольная работа «Элементы линейной алгебры и аналитической геометрии» | |
| 4.1. Основные теоретические сведения…………………………….. | |
| 4.2. Контрольные задания…………………………………………… | |
| 4.3. Пример решения контрольной работы………………………… | |
| 4.4. Вопросы для самопроверки | |
| 5. Список литературы ………………………………………………….. |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО САМОСТОЯТЕЛЬНОЙ
РАБОТЕ
Важной формой обучения любого студента является самостоятельная работа, которая состоит из изучения материала по учебникам, решения задач, самопроверки и выполнения контрольных работ. В помощь студенту проводятся лекции, практические и лабораторные занятия. Кроме того, студент может обращаться к преподавателю с вопросами.
Изучение учебника должно проводиться систематически. Переходить к следующему вопросу можно только после правильного понимания предыдущего. Особое внимание надо обращать на определение основных понятий и формулировки основных теорем. Правильному пониманию теорем помогает разбор примеров математических объектов, обладающих и не обладающих свойствами, указанными в теоремах. Полезно внимательно разбирать геометрический смысл различных понятий и утверждений. При изучении материала по учебнику полезно вести конспект, на полях которого отмечать вопросы для консультации с преподавателем.
Составление листа, содержащего важнейшие и наиболее часто используемые формулы курса не только помогает их запоминанию, но и дает возможность использовать этот лист как справочник при решении задач.
Чтение учебника должно сопровождаться решением задач, для чего следует завести специальную тетрадь. При решении задач надо обосновывать каждый этап решения, исходя из теоретических положений курса.
Решение задач надо записывать подробно, вычисления располагать в строгом порядке и обязательно выполнять проверку.
Умение решать задачи необходимо для хорошего усвоения теории, но не является доказательством такого усвоения, так как часто при решении задач формулы и утверждения используются чисто механически.
После изучения какой-либо темы следует провести самопроверку, для чего воспроизвести по памяти основные понятия, определения, формулы и формулировки теорем, вспомнить их выводы.
Если в процессе работы у студента возникают вопросы, которые не удается разрешить самостоятельно, то он может обратиться к преподавателю за письменной или устной консультацией.
В процессе изучения курса математики студент должен выполнить ряд контрольных работ, главная цель которых – оказать студенту помощь в его работе. Контрольные работы должны выполняться самостоятельно. Это дает рецензенту возможность указать студенту на недостатки в его работе, в усвоении им учебного материала.
На экзаменах и зачетах выясняется усвоение теоретических и прикладных вопросов программы и умение применять полученные знания к решению задач. При подготовке к экзамену учебный материал рекомендуется повторять по учебнику и конспекту.
ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ КОНТРОЛЬНОЙ
РАБОТЫ
При выполнении контрольных работ следует придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, могут быть не зачтены и возвращены студенту для доработки.
1. Каждую контрольную работу следует выполнять в отдельной тетради чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.
2. На обложке тетради должны быть ясно написаны номер контрольной работы, название дисциплины, фамилия, имя, отчество студента, номер зачетной книжки, номер варианта, специальность и группа, в которой обучается студент. В конце работы следует проставить дату ее выполнения и расписаться.
3. Для студентов заочной формы обучения номер варианта контрольной работы соответствует последней цифре номера зачетной книжки. Если номер зачетной книжки оканчивается цифрой «0», то студент выполняет 10-й вариант. Студенты-дневники получают номер варианта по усмотрению преподавателя.
4. В работу включаются все задачи строго по положенному варианту. Работа, содержащая не все задачи варианта или задачи не своего варианта, не зачитывается.
5. Решения задач надо располагать в порядке номеров, указанных в задании, сохраняя номера задач. Перед решением каждой задачи надо выписать полностью ее условие. Решения задач излагать подробно и аккуратно, объясняя все действия и делая необходимые чертежи.
6. Если работа не зачтена или сделаны замечания по решению задач, следует выполнить работу над ошибками в той же тетради. В связи с этим рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех исправлений и дополнений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА ДЛЯ
САМОСТОЯТЕЛЬНОЙ РАБОТЫ
2. Данко, П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевников. В 2-х ч. Ч. 1. – 4-е изд., испр. и доп. – М.:… 3. Кудрявцев, В.А. Краткий курс высшей математики / В.А. Кудрявцев, Б.П.… 4. Меркулов, В.А. Курс высшей математики. Избранные разделы: учеб. пособие / В.А. Меркулов. – Волгоград: ВолгГАСУ,…Элементы линейной алгебры
Матрицы
. Числа aij, где i = 1, 2, …, m, j = 1, 2, …, n, называются элементами матрицы… В случае, если , матрица называется прямоугольной размера . Если , то матрица А называется матрицей-строкой:Линейные операции над матрицами
1. Суммой двух матриц А и В одинаковых порядков m и n называется матрица С = А + В тех же порядков m и n, элементы которой равны суммам соответствующих элементов слагаемых:
cij = aij + bij,
где i = 1, 2, …, m, j = 1, 2, …, n.
2. Разностью двух матриц А и В одинаковых порядков m и n называется матрица С = А – В тех же порядков m и n, элементы которой равны разностям соответствующих элементов слагаемых:
cij = aij – bij,
где i = 1, 2, …, m, j = 1, 2, …, n.
3. Произведением матрицы А на действительное число a называется матрица В, элементы которой равны произведениям соответствующих элементов матрицы А на это число:
bij = aaij,
где i = 1, 2, …, m, j = 1, 2, …, n.
4. При a = –1 матрица aА = (–1)А называется противоположной матрице А и обозначается –А.
Основные свойства линейных операций над матрицами
1. А + В = В + А. 2. (А + В) + С = А + (В + С).
3. (ab)А = a(bА) = b(aА). 4. a(А + В) = aА + aВ.
5. (a + b)А = aА + bА. 6. А + О = А.
7. А + (–А) = О. 8. 0 × А = А × 0 = О.
Нелинейные операции над матрицами
1. Произведением матрицы А порядков m и n на матрицу В порядков n и k называется матрица С = АВ, каждый элемент cij которой равен сумме попарных произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В:
 ,
,
где i = 1, 2, …, m, j = 1, 2, …, n.
2. Две квадратные матрицы А и В одного порядка называются перестановочными или коммутативными, если
АВ = ВА.
3. Целой положительной степенью Аk (k > 1) квадратной матрицы А называется произведение k матриц, равных А, т. е.
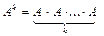 .
.
4. Если в матрице А размера 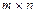 строки заменить ее столбцами, то получим матрицу размера
строки заменить ее столбцами, то получим матрицу размера  , которая называется транспонированной к матрице А и обозначается АТ.
, которая называется транспонированной к матрице А и обозначается АТ.
Основные свойства нелинейных операций над матрицами
1. А(ВС) = (АВ)С. 2. А(В + С) = АВ + АС.
3. (В + С)А = ВА + СА. 4. АЕn = EnA = A.
5. A0 = En. 6. A1 = A.
7. Ak × As = As × Ak = Ak + s. 8. (Ak)s = Aks.
9. (AT)T = A. 10. (A + B)T = AT + BT.
11. (aA)T = aAT. 12. (AB)T=BTAT.
Определители квадратных матриц
. 2. Определитель матрицы 3-го порядка – число, равное .Обратная матрица
1. Квадратная матрица  порядка
порядка 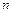 называется невырожденной, если
называется невырожденной, если
|A| ¹ 0.
В противном случае матрица А называется вырожденной.
2. Матрица А–1 называется обратной для квадратной матрицы А порядка n, если
АА–1 = А–1А = En.
3. Если А – невырожденная матрица, то она имеет обратную матрицу, которая вычисляется по формуле
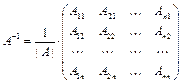 ,
,
где Aij – алгебраическое дополнение элемента aij матрица А, i = 1, 2, …, n, j = 1, 2, …, n.
Системы линейных уравнений
(1) Числа aij, где i = 1, 2, …, m, j = 1, 2, …, n, называются коэффициентами… 2. Совокупность n чисел a1, a2, …, an называется решением системы (1), если после замены неизвестных х1, х2, …, xn,…Формулы Крамера
Для решения системы трех линейных уравнений с тремя неизвестными 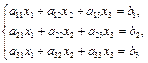 часто используются формулами Крамера:
часто используются формулами Крамера:
 ,
,  ,
, 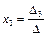 ,
,
где  ,
,  ,
,  и
и  . В этом случае система имеет единственное решение, если D ¹ 0. При n > 0 решение по формулам Крамера весьма трудоемко, что связано с вычислением определителей.
. В этом случае система имеет единственное решение, если D ¹ 0. При n > 0 решение по формулам Крамера весьма трудоемко, что связано с вычислением определителей.
Метод Гаусса
Пусть задана произвольная система линейных уравнений (1). Будем считать, что a11 ¹ 0 (в противном случае можно произвести перестановку… (2) Умножим теперь первое уравнение системы (2) на –a21 и сложим его почленно со вторым уравнением. Затем умножим первое…Элементы аналитической геометрии на плоскости
Простейшие задачи на плоскости
. 2. Если и , то координаты точки , делящей направленный отрезок в отношении ,… , .Различные виды уравнения прямой на плоскости
Угловым коэффициентом прямой называется число k = tg a. 2. Уравнение прямой, проходящей через данную точку в данном направлении : .Расстояние от точки до прямой на плоскости
Расстояние от точки 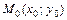 до прямой
до прямой 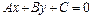 вычисляется по формуле:
вычисляется по формуле:
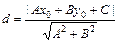 .
.
Взаимное расположение двух прямых на плоскости
. 2. Условие параллельности двух прямых: прямые и параллельны тогда и только… .Кривые второго порядка
Если фокусы и директрисы брать тремя другими способами, то получим еще три параболы (табл. 1). Таблица 1 Уравнение параболы Фокус Директриса …Рис. 3
4. Гиперболой называется геометрическое место точек плоскости, разность расстояний от которых до двух данных точек F1 и F2, называемых фокусами (|F1F2| = 2c) есть величина постоянная, равная ± 2a, где 2a < 2c.
Каноническое уравнение гиперболы (рис. 4):
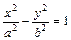 .
.
Точки 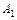 и
и 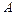 – вершины гиперболы; отрезок
– вершины гиперболы; отрезок  – действительная ось, отрезок
– действительная ось, отрезок 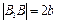 – мнимая ось; параметры
– мнимая ось; параметры  и
и  – действительная и мнимая полуоси; точки
– действительная и мнимая полуоси; точки  и
и 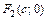 – левый и правый фокусы; число
– левый и правый фокусы; число 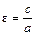 – эксцентриситет гиперболы; левый и правый фокальные радиусы для точек левой ветви гиперболы равны
– эксцентриситет гиперболы; левый и правый фокальные радиусы для точек левой ветви гиперболы равны  и
и  , а для точек правой ветви гиперболы – это
, а для точек правой ветви гиперболы – это  и
и 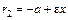 ; прямые
; прямые 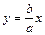 и
и 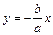 – асимптоты гиперболы. Параметры
– асимптоты гиперболы. Параметры  ,
,  и
и 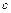 связаны равенством
связаны равенством  .
.
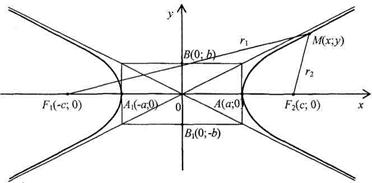
Рис. 4
Элементы векторной алгебры
Основные понятия
1. Вектором с началом в точке А и концом в точке В называется направленный отрезок 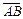 .
.
2. Длиной (модулем, абсолютной величиной) |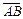 | вектора
| вектора 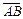 называется длина направленного отрезка.
называется длина направленного отрезка.
3. Если начало и конец вектора совпадают, то вектор  называется нулевым, а его длина равна нулю.
называется нулевым, а его длина равна нулю.
4. Вектор, длина которого равна единице, называется единичным (ортом).
5. Два и более вектора называются коллинеарными (обозначение: 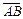 ||
||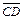 ), если они лежат на одной или параллельных прямых.
), если они лежат на одной или параллельных прямых.
6. Два вектора 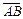 и
и 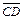 называются равными, если:
называются равными, если:
1) |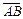 |=|
|=|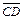 |, 2)
|, 2) 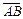 ||
||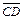 , 3)
, 3) 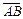
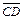 .
.
7. Из определения равенства двух векторов следует, что точка их приложения не играет никакой роли. Это означает, что векторы можно переносить в пространстве параллельно самим себе, приводя их начало в общую точку. По той же причине такие векторы можно обозначать одной буквой 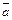 ,
, 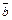 и т. д.
и т. д.
8. Вектор  называется противоположным вектору
называется противоположным вектору  , если:
, если:
1) | |=|
|=|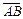 |, 2)
|, 2)  ||
||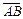 , 3)
, 3)  ¯
¯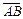 .
.
9. Вектор 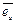 называется ортом вектора
называется ортом вектора 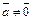 , если выполняются три условия:
, если выполняются три условия:
1) |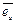 |=1,
|=1,
2) 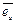 ||
||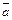 ,
,
3)  , если
, если 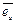
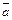 и
и  , если
, если 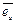 ¯
¯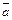 .
.
10. Векторы 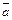 ,
, 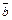 и
и 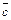 называются компланарными, если существует плоскость, которой они параллельны.
называются компланарными, если существует плоскость, которой они параллельны.
11. Углом между двумя векторами, приведенных к общему началу называется угол, который не превосходит p.
Линейные операции над векторами
1. Суммой векторов 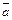 и
и 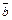 называется вектор
называется вектор 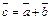 , идущий из начала первого вектора в конец второго вектора при условии, что начало второго вектора приложено к концу первого (рис. 5).
, идущий из начала первого вектора в конец второго вектора при условии, что начало второго вектора приложено к концу первого (рис. 5).

Рис. 5
Это правило называется правилом треугольника.
2. Свойства операции сложения:
1)  ,
,
2) 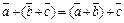 ,
,
3)  ,
,
4)  .
.
3. Первое свойство приводит к правилу параллелограмма сложения векторов: сумма двух векторов изображается диагональю параллелограмма, проведенной из общего начала (рис. 6).
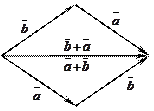 |
Рис. 6
4. Разностью векторов 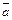 и
и 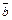 называется вектор
называется вектор 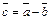 , равный сумме вектора
, равный сумме вектора 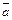 и
и  , противоположного вектору
, противоположного вектору 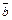 , т. е.
, т. е.
 .
.
Из определения видно, что этот вектор изображается второй диагональю параллелограмма, идущей из конца вычитаемого вектора в конец уменьшаемого при условии, что оба вектора 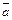 и
и 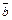 приведены к общему началу (рис. 7).
приведены к общему началу (рис. 7).
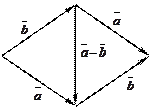
Рис. 7
5. Произведением вектора 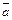 на число a называется вектор
на число a называется вектор 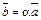 , удовлетворяющий трем условиям:
, удовлетворяющий трем условиям:
1) 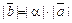 ,
,
2) 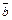 ||
||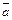 ,
,
3) 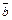
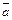 , если a > 0,
, если a > 0, 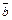 ¯
¯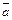 , если a < 0 и
, если a < 0 и 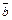 =
= , если a = 0.
, если a = 0.
6. Свойства операции умножения вектора на число:
1) 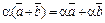 ,
,
2)  ,
,
3) 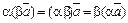 .
.
7. Множество векторов с тремя линейными операциями, удовлетворяющих свойствам п. 2 и п. 6, называется линейным (векторным) пространством. Обозначение: Rn.
Базис векторов. Координаты вектора относительно базиса
= a1 + a2 + … + an, которые называются линейной комбинацией векторов , , …, с коэффициентами a1,… 2. Система векторов , , …, называется линейно независимой, если равенствоДействия над векторами в координатной форме
. 2. Два вектора и равны тогда и только тогда, когдаРис. 8
16. Смешанное произведение векторов  ,
,  и
и  есть число
есть число  , равное скалярному произведению вектора
, равное скалярному произведению вектора  на вектор
на вектор 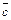 и вычисляемое по формуле:
и вычисляемое по формуле:
 .
.
17. Условие компланарности векторов: три вектора 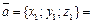
 ,
,  и
и 
 компланарны тогда и только тогда, когда
компланарны тогда и только тогда, когда
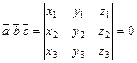 .
.
18. Геометрический смысл смешанного произведения: смешанное произведение трех векторов  , взятое по модулю, численно равно объему параллелепипеда, построенного на этих векторах как на ребрах (рис. 9), т. е.
, взятое по модулю, численно равно объему параллелепипеда, построенного на этих векторах как на ребрах (рис. 9), т. е.
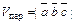 .
.
Объем пирамиды, построенной на этих векторах, равен
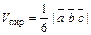 .
.

Рис. 9
Элементы аналитической геометрии в пространстве
Различные виды уравнения плоскости
, где – нормальный вектор (ненулевой вектор, перпендикулярный плоскости). 2. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору (нормальный вектор):Взаимное расположение двух плоскостей
. 2. Условия параллельности двух плоскостей: плоскость с нормальным вектором и… .Расстояние от точки до плоскости
Расстояние от точки  до плоскости
до плоскости 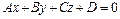 с нормальным вектором
с нормальным вектором  вычисляется по формуле:
вычисляется по формуле:
 .
.
Различные виды уравнений прямой в пространстве
где и – плоскости с нормальными векторами и соответственно. 2. Канонические уравнения прямой:Взаимное расположение двух прямых в пространстве
. 2. Условия параллельности двух прямых в пространстве: прямая с направляющим… .Взаимное расположение прямой с плоскостью
. 2. Условие параллельности прямой и плоскости: прямая с направляющим вектором и… .Рис. 10
2) По определению медианы точка М медианы CМ делит сторону АВ пополам. Следовательно, ее координаты определяются по формулам деления отрезка пополам
 ,
, 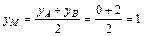 .
.
Таким образом, получена точка М(2; 1).
Уравнение медианы CМ найдем как уравнение прямой, проходящей через две заданные точки C и М, по формуле
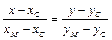 , т. е.
, т. е. 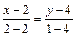 или
или  .
.
По свойству пропорции отсюда следует уравнение CМ
 или
или 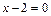 .
.
3) Уравнение высоты СH как прямой, проходящей через точку С перпендикулярно стороне АВ, будем искать в виде
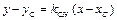 ,
,
где угловой коэффициент  найдем из условия перпендикулярности прямых СH и АВ
найдем из условия перпендикулярности прямых СH и АВ
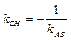 .
.
Угловой коэффициент 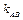 определим, используя формулу углового коэффициента прямой
определим, используя формулу углового коэффициента прямой
 ,
,
следовательно,
 .
.
Уравнение высоты примет теперь вид
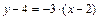 или
или 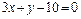 .
.
4) Аналогично, уравнение прямой L, проходящей через вершину С параллельно стороне АВ, будем искать в виде
 ,
,
где угловой коэффициент  прямой L найдем из условия параллельности прямых L и AB
прямой L найдем из условия параллельности прямых L и AB
 .
.
Уравнение прямой L примет вид
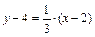 или
или  .
.
5) Длину высоты СН найдем, используя формулу расстояния от точки С до прямой АВ
 ,
,
где  есть общее уравнение стороны АВ. Найдем уравнение стороны АВ по формуле
есть общее уравнение стороны АВ. Найдем уравнение стороны АВ по формуле
 , т. е.
, т. е.  , или
, или  .
.
Подставляя в найденное уравнение координаты точки С, получим
 (ед.).
(ед.).
6) Из рис. 10 видно, что внутренний угол А треугольника АВС есть угол, на который нужно повернуть сторону АВ в положительном направлении (т. е. против часовой стрелки) до совмещения ее со стороной АС. Поэтому тангенс угла А найдем по формуле
 .
.
Угловой коэффициент 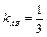 (найден в п. 3). Аналогично найдем
(найден в п. 3). Аналогично найдем
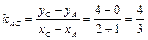 ,
,
тогда
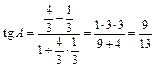 ,
,
следовательно,
 (рад.).
(рад.).
Ответ: 1) длина стороны АВ:  ед.; 2) уравнение медианы CМ:
ед.; 2) уравнение медианы CМ:  ; 3) уравнение высоты СН:
; 3) уравнение высоты СН: 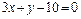 ; 4) уравнение прямой L:
; 4) уравнение прямой L:  ; 5) длина высоты СН:
; 5) длина высоты СН: 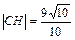 ед.; 6) величина внутреннего угла А:
ед.; 6) величина внутреннего угла А:  рад.
рад.
Задание 4. Составить уравнение и построить линию, для каждой точки которой выполняется следующее условие: отношение расстояний до точки F(–1; 0) и прямой 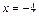 равно
равно  .
.
 Решение. Сделаем схематический чертеж по условию задачи (рис. 11).
Решение. Сделаем схематический чертеж по условию задачи (рис. 11).
Рис. 11
Предположим, что М(x; y) – текущая точка искомой линии. Тогда точка N(–4; y) является ее проекцией на прямой x = –4.
По условию задачи выполняется следующее отношение расстояний
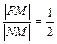 или
или  .
.
Используя формулу расстояния между двумя точками, выразим полученное буквенное равенство в координатной форме и преобразуем его к виду канонического уравнения одной из кривых второго порядка
|
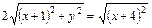 или
или 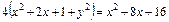 ,
,
или  .
.
Получили каноническое уравнение эллипса:  , у которого полуоси есть
, у которого полуоси есть 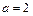 и
и 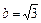 .
.
Построим линию по ее уравнению (рис. 12).
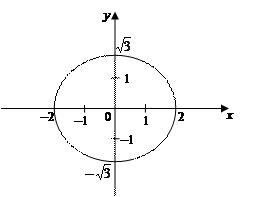
Рис. 12
Ответ: 
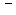 эллипс.
эллипс.
Задание 5. Написать разложение вектора  по векторам
по векторам  ,
, 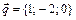 ,
, 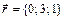 .
.
Решение. Требуется представить вектор 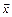 в виде
в виде 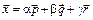 , где a, b, g – числа. По правилу умножения вектора на число получим
, где a, b, g – числа. По правилу умножения вектора на число получим
 ,
,  ,
, 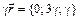 .
.
По правилу сложения векторов получим
 .
.
По определению равенства двух векторов получим систему линейных уравнений относительно неизвестных a, b, g
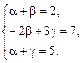
Решим систему по формулам Крамера. Составим четыре определителя D, D1, D2, D3 третьего порядка и вычислим их по правилу треугольников. Так как
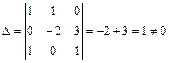 ,
,
то система имеет единственное решение;
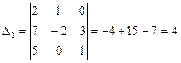 ,
,  ,
,
 .
.
По формулам Крамера получим
 ,
,  ,
, 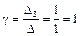 .
.
Таким образом, искомое разложение имеет вид
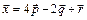 .
.
Ответ: 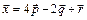 .
.
Задание 6. Даны вершины A1(1; –1; 2), A2(2; 1; 2), A3(1; 1; 4),
A4(6; –3; 8) пирамиды A1A2A3A4. Найти: 1) величину угла между ребрами A1A3 и A1A4; 2) площадь грани A1A2A3; 3) уравнение плоскости, содержащей грань A1A2A3; 4) уравнения высоты пирамиды, проведенной через вершину A4. Сделать схематический чертеж.
Решение. Сделаем схематический чертеж (рис. 13).
1. Найдем векторы  и
и 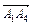 , проходящие через 2 заданные точки:
, проходящие через 2 заданные точки:
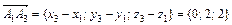 ,
,
 .
.
Находим косинус угла между векторами по формуле:
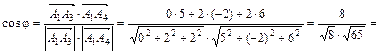
 ,
,
следовательно, угол  (рад.).
(рад.).
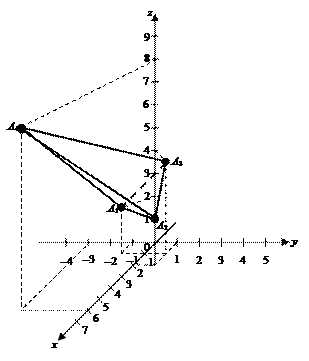 |
Рис. 13
2. Гранью A1A2A3 пирамиды A1A2A3A4 является треугольник A1A2A3, площадь которого определим по формуле:
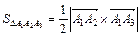 .
.
Координаты вектора  (см. п. 1). Аналогично найдем координаты вектора
(см. п. 1). Аналогично найдем координаты вектора 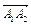 :
:
 .
.
Вычислим теперь векторное произведение векторов 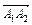 и
и  :
:
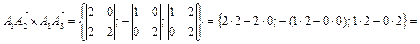
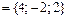 .
.
Тогда длина векторного произведения равна:
 .
.
Таким образом, окончательно получим:
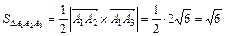 (кв. ед.).
(кв. ед.).
3. Уравнение искомой плоскости составим как уравнение плоскости, проходящей через три данные точки A1, A2, A3 в форме определителя 3-го порядка:
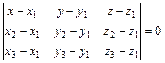 или
или  .
.
Приведем это уравнение плоскости к общему уравнению:

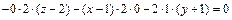 ,
,
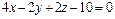 ,
,
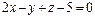 .
.
4. Уравнения высоты, опущенной из точки А4 на грань А1А2А3 найдем как прямую, проходящую через точку А4 перпендикулярно плоскости А1А2А3 в форме канонических уравнений прямой
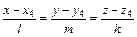 ,
,
где вектор  является направляющем вектором прямой (коллинеарен прямой). В п. 3 было найдено уравнение плоскости А1А2А3:
является направляющем вектором прямой (коллинеарен прямой). В п. 3 было найдено уравнение плоскости А1А2А3: 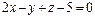 , следовательно, ее нормальным вектором является вектор
, следовательно, ее нормальным вектором является вектор
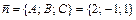 .
.
Т. к. вектор 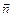 коллинеарен высоте, то его можно выбрать в качестве направляющего вектора
коллинеарен высоте, то его можно выбрать в качестве направляющего вектора  прямой. Следовательно, искомые уравнения высоты имеют вид:
прямой. Следовательно, искомые уравнения высоты имеют вид:
 .
.
Ответ: 1) величина угла между ребрами A1A3 и A1A4:  рад.; 2) площадь грани A1A2A3:
рад.; 2) площадь грани A1A2A3: 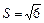 кв. ед.; 3) уравнение плоскости A1A2A3:
кв. ед.; 3) уравнение плоскости A1A2A3: 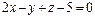 ; 4) уравнения высоты из вершины A4:
; 4) уравнения высоты из вершины A4:  .
.
4.4. Вопросы для самопроверки
1. Определение числовой матрицы. Понятие о матрице-строке, матрице-столбце, квадратной матрице, главной и побочной диагоналях квадратной матрицы.
2. Определение единичной и нулевой матрицы. Определение равенства двух матриц.
3. Линейные операции над матрицами. Основные свойства.
4. Нелинейные операции над матрицами. Основные свойства. Определение коммутативных матриц.
5. Определители квадратных матриц 2-го, 3-го и т. д. n-го порядка.
6. Определение минора и алгебраического дополнения элемента определителя.
7. Определение обратной матрицы. Невырожденные матрицы. Формула нахождения обратной матрицы.
8. Основные понятия системы m линейных уравнений с n неизвестными. Элементарные преобразования системы.
9. Решение систем линейных уравнений по формулам Крамера.
10. Ранг матрицы. Условие совместности линейной системы.
11. Решение систем линейных уравнений методом Гаусса.
12. Прямоугольные декартовы координаты точки на плоскости.
13. Три основные задачи на плоскости: расстояние между двумя точками, деление направленного отрезка в данном отношении, площадь треугольника.
14. Линия как геометрическое место точек. Уравнение линии. Параметрические уравнения линии.
15. Угол наклона и угловой коэффициент прямой. Различные виды уравнения прямой на плоскости.
16. Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности двух прямых на плоскости.
17. Расстояние от данной точки до данной прямой.
18. Кривые второго порядка: окружность, парабола, эллипс и гипербола.
19. Векторы: основные понятия.
20. Линейные операции над векторами и их свойства.
21. Прямоугольные декартовы координаты точки в пространстве.
22. Линейно зависимые и независимые векторы. Понятие n-мерного векторного пространства. Базис векторного пространства. Разложение вектора по ортонормированному базису. Декартовы координаты вектора. Формулы перехода от одного базиса к другому.
23. Линейные операции над векторами в координатной форме. Условие коллинеарности двух векторов.
24. Скалярное произведение векторов. Основные свойства и следствия из них.
25. Векторное произведение векторов. Свойства. Геометрический смысл векторного произведения.
26. Смешанное произведение векторов. Условие их компларности. Геометрический смысл смешанного произведения.
27. Различные виды уравнения плоскости.
28. Неполные уравнения плоскости.
29. Взаимное расположение двух плоскостей. Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей.
30. Расстояние от точки до плоскости.
31. Различные виды уравнений прямой в пространстве.
32. Взаимное расположение двух прямых в пространстве. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых.
33. Взаимное расположение прямой и плоскости. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости.
Список литературы
1. Лунгу, К. Н. Сборник задач по высшей математике. 1 курс / К. Н. Лунгу [и др.]. – М.: Рольф, 2001. – 576 с.
2. Методические указания для студентов специальности 060800 «Экономика и управление на предприятии (строительство)» заочной формы обучения по дисциплине «Высшая математика» / ВИСТех (филиал) ВолгГАСУ; [сост. Е.В. Абрамов, Е.Д. Илларионова, Е.Ю. Волченко]. – Волжский: ВИСТех (филиал) ВолгГАСУ, 2010. – 95 с.
3. Письменный, Д. Т. Конспект лекций по высшей математике. 1 часть. / Д. Т. Письменный. – М.: Рольф, 2001. – 288 с.
4. Рябушко, А. П. Сборник индивидуальных заданий по высшей математике. Часть 1 / А. П. Рябушко [и др.]. – Мн.: Выш. шк., 1992
План уч.-метод. докум. 2012 г., поз. № 20
Составители: Е. В. Абрамов, Д. П. Торшин
элементы линейной алгебры и
аналитической геометрии
Методические указания по самостоятельной работе и
задания контрольной работы
для студентов заочной формы обучения
по направлениям «Строительство» и
«Наземные транспортно-технологические комплексы»
Редактор Е. В. Румянцева
Подписано в печать 19.05.2010 г. Формат 60 х 84 / 16.
Гарнитура Times New Roman. Бумага UNION PRINTS.
Печать трафаретная.
Усл. печ. л. 5,52. Уч.-изд. л. 5,94. Т. 62 экз.
 |
Волжский институт строительства и технологий (филиал)
Волгоградского государственного архитектурно-строительного университета
404111 г. Волжский, пр. Ленина, 72
– Конец работы –
Используемые теги: Элементы, ной, алгебры, аналитической, геометрии0.081
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Элементы линейной алгебры и аналитической геометрии
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов