Метод найменших квадратів
Нехай емпірична формула має вигляд  , де
, де  ,
,  , …,
, …,  ─ невідомі коефіцієнти. Треба знайти такі значення коефіцієнтів
─ невідомі коефіцієнти. Треба знайти такі значення коефіцієнтів  , за яких крива якомога ближче проходитиме до всіх точок
, за яких крива якомога ближче проходитиме до всіх точок  ,
,  , …,
, …,  , знайдених експериментально. Зрозуміло, що жодна з експериментальних точок не задовольняє точно рівнянню. Відхилення від підстановки координат
, знайдених експериментально. Зрозуміло, що жодна з експериментальних точок не задовольняє точно рівнянню. Відхилення від підстановки координат  у рівняння дорівнюватимуть величинам
у рівняння дорівнюватимуть величинам  . За методом найменших квадратів найкращі значення коефіцієнтів
. За методом найменших квадратів найкращі значення коефіцієнтів  ті, для яких сума квадратів відхилень
ті, для яких сума квадратів відхилень  .
.
Вибрати емпіричну формулу для нелінійних залежностей графічним методом часто буває важко. Тоді вдаються до перевірки аналітичних критеріїв існування певної залежності. Найпростіші необхідні умови залежностей подано в таблиці.
| № пор. | Емпірична формула | 
| 
| Спосіб вирівнювання |

| 
| 
| ||

| 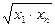
| 
|  , де , де  , ,  , ,  , , 
| |
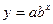
| 
| 
|  , де , де  , ,  , , 
| |

| 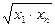
| 
| 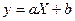 , де , де 
| |

| 
| 
| 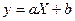 , де , де 
| |

| 
| 
| 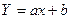 , де , де 
| |

| 
| 
|  , де , де  , , 
|
Умови перевіряють наступним чином. На заданому відрізку вибирають дві точки, розміщені якомога далі одна від одної, наприклад,  ,
, 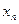 . Потім, залежно від типу залежності, що перевіряється, обчислюють значення
. Потім, залежно від типу залежності, що перевіряється, обчислюють значення  і
і  . Далі, користуючись даною таблицею значень
. Далі, користуючись даною таблицею значень  , для значення
, для значення  знаходять відповідне йому значення
знаходять відповідне йому значення  . Якщо
. Якщо  немає в таблиці, то
немає в таблиці, то  знаходять наближено з графіка або за допомогою лінійної інтерполяції
знаходять наближено з графіка або за допомогою лінійної інтерполяції  , де
, де  і
і  ─ проміжні значення, між якими лежить
─ проміжні значення, між якими лежить 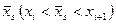 . Обчисливши
. Обчисливши  , знаходять величину
, знаходять величину  . Якщо ця величина велика, то відповідна емпірична формула не придатна для апроксимації заданих даних. З кількох придатних формул перевагу надають тій, для якої відхилення
. Якщо ця величина велика, то відповідна емпірична формула не придатна для апроксимації заданих даних. З кількох придатних формул перевагу надають тій, для якої відхилення  якомога менше.
якомога менше.
Вхідні дані повинні бути впорядковані за зростанням аргументу.