Начальной крайней точки
Рассмотрим задачу линейного программирования в канонической форме:
 , (зк)
, (зк)
где 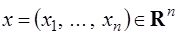 – неизвестная переменная,
– неизвестная переменная,  и
и  – заданные векторы,
– заданные векторы, 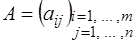 – заданная матрица размера
– заданная матрица размера  . Будем считать, что
. Будем считать, что  (если
(если 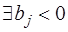 , то умножим обе части
, то умножим обе части  -го уравнения на (-1)).
-го уравнения на (-1)).
Рассмотрим вспомогательную задачу, добавляя искусственные переменные 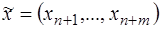 и единичную матрицу
и единичную матрицу 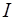 :
:
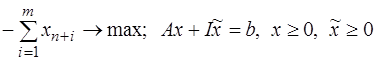 .
. 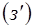
Точка 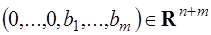 является начальной крайней точкой для вспомогательной задачи
является начальной крайней точкой для вспомогательной задачи 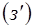 . Решение задачи
. Решение задачи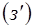 имеет вид:
имеет вид:  . Тогда точка
. Тогда точка  является начальной крайней точкой исходной задачи (зк).
является начальной крайней точкой исходной задачи (зк).
Пример 3. Решить задачу линейного программирования симплекс-методом, находя начальную крайнюю точку методом искусственного базиса.
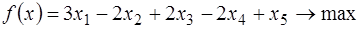 ;
;
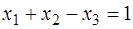 ,
,
 ,
,
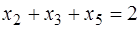
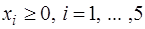 .
.
Решение: Составим вспомогательную задачу:
 ;
;
 ,
,
 ,
,

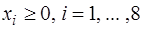 .
.
Начальной крайней точкой вспомогательной задачи является точка 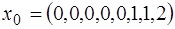 . Заметим, что базисная матрица вспомогательной задачи есть единичная матрица. Поэтому
. Заметим, что базисная матрица вспомогательной задачи есть единичная матрица. Поэтому 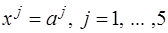 . Построим симплексную таблицу:
. Построим симплексную таблицу:

| -1 | -1 | -1 | 
| |||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| 
| ||

| -1 | -1 | |||||||||

| -1 | -1 | |||||||||

| -1 | ||||||||||

| -4 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | ||

| -1 | -1 | -1 | -1 | -1 |
В последней строке содержится 5 одинаковых отрицательных чисел. Для определенности в качестве разрешающего столбца возьмем столбец  . Так как в соответствующем столбце содержится только один положительный элемент, то соответствующая строка
. Так как в соответствующем столбце содержится только один положительный элемент, то соответствующая строка  будет разрешающей. Исключаем из базиса вектор
будет разрешающей. Исключаем из базиса вектор  и заменяем его на
и заменяем его на 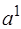 . Строим новую симплексную таблицу:
. Строим новую симплексную таблицу:

| -1 | -1 | -1 | 
| |||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| 
| ||

| -1 | ||||||||||

| -1 | -1 | |||||||||

| -1 | ||||||||||

| -3 | -2 | -1 | -1 | -1 | -1 | |||||

| -2 | -1 | -1 |
Минимальным отрицательным элементом в последней строке является элемент -2, соответствующий вектору  . Столбец
. Столбец  будет разрешающим. В этом столбце имеется два положительных элемента, поэтому заполняем последний столбец таблицы и находим наименьшее из получившихся чисел. Соответствующая строка
будет разрешающим. В этом столбце имеется два положительных элемента, поэтому заполняем последний столбец таблицы и находим наименьшее из получившихся чисел. Соответствующая строка  является разрешающей.
является разрешающей.
Выводим из базиса вектор  и строим таблицу для нового базиса
и строим таблицу для нового базиса  :
:

| -1 | -1 | -1 | 
| |||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| 
| ||

| |||||||||||

| -1 | ||||||||||

| -1 | -1 | -1 | ||||||||

| -1 | -2 | -1 | -1 | |||||||

| -2 | -1 |
Минимальным отрицательным элементом в последней строке является элемент -2, соответствующий вектору  . Столбец
. Столбец  будет разрешающим. В этом столбце имеется одно положительное число, поэтому строка
будет разрешающим. В этом столбце имеется одно положительное число, поэтому строка  является разрешающей. Строим таблицу для базиса
является разрешающей. Строим таблицу для базиса 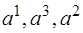 :
:

| -1 | -1 | -1 | 
| |||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| 
| ||

| |||||||||||

| 
| 
| 
| 
| 
| ||||||

| 
| 
| 
| 
| 
| ||||||

| |||||||||||

|
Так как 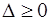 , то точка
, то точка 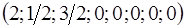 является решением вспомогательной задачи, а точка
является решением вспомогательной задачи, а точка  является начальной крайней точкой исходной задачи. Используя полученные разложения векторов по базису
является начальной крайней точкой исходной задачи. Используя полученные разложения векторов по базису 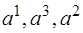 , строим симплексную таблицу исходной задачи:
, строим симплексную таблицу исходной задачи:

| -2 | -2 | 
| |||||
| базис | 
| 
| 
| 
| 
| 
| ||

| ||||||||

| 
| 
| 
| |||||

| -2 | 
| 
| 
| ||||

| -2 | |||||||

| -1 |
Последняя строка содержит один отрицательный элемент, соответствующий вектору  . Вычисляем элементы последнего столбца и выбираем наименьший положительный, соответствующий разрешающей строке
. Вычисляем элементы последнего столбца и выбираем наименьший положительный, соответствующий разрешающей строке  . Для нового базиса
. Для нового базиса 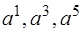 строим таблицу:
строим таблицу:

| -2 | -2 | 
| |||||
| базис | 
| 
| 
| 
| 
| 
| ||

| ||||||||

| -1 | |||||||

| -1 | |||||||

| ||||||||

|
Так как 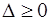 , то
, то  является решением задачи,
является решением задачи, 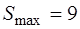 .
.
Замечание. В данной задаче можно было ограничиться введением одной искусственной переменной  , так как два последних столбца матрицы
, так как два последних столбца матрицы 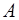 задачи являются столбцами единичной матрицы. Тогда число шагов значительно бы уменьшилось. ●
задачи являются столбцами единичной матрицы. Тогда число шагов значительно бы уменьшилось. ●
Пример 4. Решить задачу линейного программирования:
 ; (з)
; (з)
 ,
,
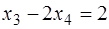 ,
,
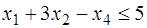 ,
,
 .
.
На первом шаге приведем данную задачу к канонической форме, введя дополнительные переменные  . Получим следующую задачу:
. Получим следующую задачу:
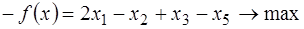 ; (з1)
; (з1)
 ,
,
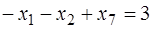 ,
,
 ,
,
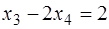 ,
,  .
.
Полученную задачу линейного программирования (з1) в канонической форме будем решать методом искусственного базиса. Для этого рассмотрим вспомогательную задачу, добавляя искусственные переменные 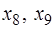 :
:
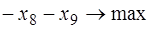 ; (з2)
; (з2)
 ,
,
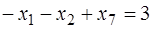 ,
,
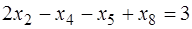 ,
,
 ,
,  .
.
Начальная крайняя точка задачи (з2)  . Базисные векторы
. Базисные векторы
 .
.
Составим симплексную таблицу для задачи (з2):

| -1 | -1 | 
| |||||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| ||

| -1 | 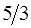
| ||||||||||

| -1 | -1 | ||||||||||

| -1 | -1 | -1 | 
| ||||||||

| -1 | -2 | ||||||||||

| -5 | -2 | -1 | -1 | -1 | |||||||

| -2 | -1 |
Из таблицы видно, что разрешающим столбцом является столбец  , а разрешающей строкой
, а разрешающей строкой  . Заменяем в базисе вектор
. Заменяем в базисе вектор  на вектор
на вектор  и строим новую симплексную таблицу:
и строим новую симплексную таблицу:

| -1 | -1 | 
| |||||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| ||

| 
| 
| 
| 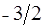
| ||||||||

| 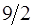
| -1 | 
| 
| 
| |||||||

| 
| 
| 
| 
| ||||||||

| -1 | -2 | ||||||||||

| -2 | -1 | -1 | |||||||||

| -1 |
Заменяем в базисе вектор  на вектор
на вектор  и строим новую симплексную таблицу:
и строим новую симплексную таблицу:

| -1 | -1 | 
| |||||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| ||

| 
| 
| 
| 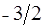
| ||||||||

| 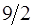
| -1 | 
| 
| 
| |||||||

| 
| 
| 
| 
| ||||||||

| -2 | |||||||||||

| ||||||||||||

|
Вектор 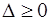 , поэтому точка
, поэтому точка 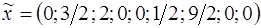 является решением вспомогательной задачи (з2). Тогда точка
является решением вспомогательной задачи (з2). Тогда точка  является начальной крайней точкой задачи линейного программирования в канонической форме (з1).
является начальной крайней точкой задачи линейного программирования в канонической форме (з1).
Приступим к решению задачи (з1). Составим первую симплексную таблицу для начальной крайней точки  . Разложения векторов
. Разложения векторов 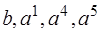 возьмем из последней симплексной таблицы:
возьмем из последней симплексной таблицы:

| 
| |||||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| ||

| 
| 
| 
| |||||||

| 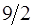
| -1 | 
| 
| ||||||

| -1 | 
| 
| 
| ||||||

| -2 | |||||||||

| 
| -1 | 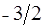
| 
| ||||||

| -2 | 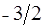
| 
|
Из таблицы видно, что разрешающим столбцом является столбец  , а разрешающей строкой
, а разрешающей строкой  . Заменяем в базисе вектор
. Заменяем в базисе вектор  на вектор
на вектор  и строим новую симплексную таблицу:
и строим новую симплексную таблицу:

| 
| |||||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| ||

| 
| 
| 
| |||||||

| ||||||||||

| -1 | 
| 
| 
| ||||||

| -2 | |||||||||

| 
| -1 | 
| 
| ||||||

| 
| 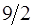
|
Далее заменяем в базисе вектор  на вектор
на вектор  и строим новую симплексную таблицу:
и строим новую симплексную таблицу:

| 
| |||||||||
| базис | 
| 
| 
| 
| 
| 
| 
| 
| ||

| ||||||||||

| ||||||||||

| -1 | |||||||||

| 
| |||||||||

| -1 | 
| ||||||||

| 
|
Так как 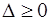 , то точка
, то точка 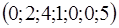 является решением задачи (з1). Тогда точка
является решением задачи (з1). Тогда точка 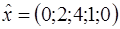 является решением исходной задачи (з).
является решением исходной задачи (з).
Ответ: 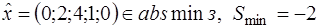 . ●
. ●