Вариационного исчисления.
Рассмотрим некоторое функциональное пространство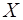 
. Пусть каждому элементу 
поставлено в соответствие число 
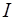. Тогда говорят, что на множестве 
задан функционал 
.
Линейное пространство 
называется нормированным, если на 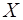определен функционал 
, называемый нормой и удовлетворяющий условиям:
а) 
, причем 
;
б) 
;
в) 
.
Будем рассматривать следующие функциональные пространства:
1) 
- пространство функций, непрерывных на отрезке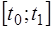 
с введенной в нем нормой 
;
2) 
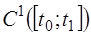- пространство функций, имеющих непрерывную производную на отрезке 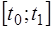с нормой
.
Определение. Простейшей задачей классического вариационного исчисления (КВИ) называется следующая экстремальная задача в пространстве :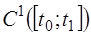
. (з)
Здесь 
- функция трех переменных, называемая интегрантом, отрезок 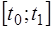фиксирован и конечен, 
. ▲
Определение. Функции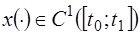 
, удовлетворяющие краевым условиям 
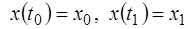, называются допустимыми. ▲
Рис. 8.1
Определение. Говорят, что допустимая функция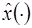 
доставляет слабый локальный минимум (максимум) в задаче (з), пишут: 
, если 
такое, что для любой допустимой функции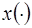 
, удовлетворяющей условию 
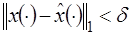, выполнено неравенство
. ▲
Теорема. Пусть функция 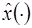доставляет слабый локальный экстремум в поставленной задаче (з) 
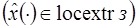, а функции 
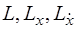непрерывны как функции трех переменных в некоторой окрестности множества 
. Тогда 
и функция 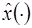удовлетворяет уравнению Эйлера:
. (1)
Здесь использованы следующие обозначения:
.
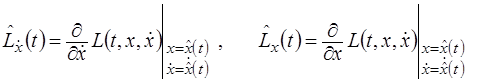Доказательство: Возьмем произвольную, но фиксированную функцию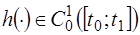 
, где
.
Рассмотрим функцию одной вещественной переменной
.
Функция 
является допустимой для любого 
. Так как 
, то функция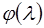 
имеет экстремум в точке 
.
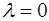Положим 
. Тогда
.
Из условий гладкости, наложенных на функции 
, следует, что функции 
и 
дифференцируемы в некотором прямоугольнике 
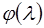, поэтому функция дифференцируема в нуле и по теореме Ферма 
.
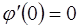Продифференцируем функцию :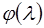
,
. (2)
На следующем этапе доказательства теоремы сформулируем и докажем вспомогательное утверждение.
Лемма Дюбуа-Реймона.
Пусть функции 
непрерывны на отрезке 
и
.
Тогда 
и выполнено равенство
.
Доказательство леммы: Возьмем функцию 
такую, что
.
Такая функция существует, так как из первого условия функция 
определяется с точностью до константы, а выбором константы можно удовлетворить второе условие. Тогда для любой функции 
по условию леммы справедливы равенства:
.
Рассмотрим функцию 
. Эта функция принадлежит пространству 
. Действительно,
.
Далее, 
.
Тогда для функции 
также должно выполняться равенство 
. Откуда следует, что 
. Поэтому и 
.
Теперь из леммы Дюбуа-Реймона и равенства (2) следует утверждение теоремы. ■
Уравнение (1) представляет собой дифференциальное уравнение второго порядка, так что его общее решение должно зависеть от двух произвольных постоянных. Значения этих постоянных определяются из граничных условий
.
Следует отметить, что краевая задача
не всегда имеет решение, а если решение существует, то оно может быть не единственным.
Определение. Функции, удовлетворяющие уравнению Эйлера задачи (з), называются экстремалями, а допустимые функции, удовлетворяющие уравнению Эйлера, называются допустимыми экстремалями. ▲
Интегралы уравнения Эйлера.
1. Если интегрант 
не зависит явно от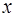 
, то имеет место интеграл импульса
.
2. Если интегрант 
не зависит явно от 
, то имеет место интеграл энергии
.
Для доказательства интеграла энергии умножим обе части равенства (1) на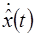 
:
Отметим, что при выводе интеграла энергии использовалось дополнительное предположение о существовании второй производной 
.
Пример 1. 
.
Решение: Интегрант задачи равен 
.
Уравнение Эйлера имеет вид:
.
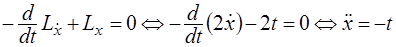Общее решение дифференциального уравнения Эйлера:
.
Постоянные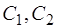 
найдем из граничных условий:
.
Откуда получаем 
. Единственная допустимая экстремаль задачи имеет вид:
.
Покажем, что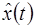 
доставляет абсолютный минимум в задаче, т.е. покажем, что для любой допустимой функции 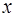выполнено неравенство 
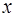. Представим функцию в виде: 
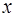. Так как функция должна удовлетворять краевым условиям задачи, то для функции 
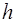краевые условия будут нулевыми: 
.
Рассмотрим разность 
:
.
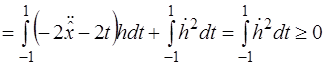Таким образом, для любой допустимой функции разность неотрицательна.
Ответ: 
.●