Теорема Куна-Таккера.
1) Пусть 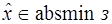 . - точка абсолютного минимума в задаче выпуклого программирования. Тогда существует ненулевой вектор множителей Лагранжа
. - точка абсолютного минимума в задаче выпуклого программирования. Тогда существует ненулевой вектор множителей Лагранжа 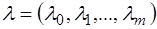 такой, что выполняются условия:
такой, что выполняются условия:
а) принцип минимума для функции Лагранжа  :
:
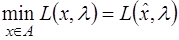 ;
;
б) условия дополняющей нежесткости:
 ;
;
в) условия неотрицательности:
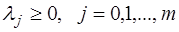 .
.
2) Если для допустимой точки 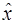 выполнены условия а), б), в) и
выполнены условия а), б), в) и 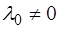 , то
, то 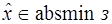 .
.
3) Если для допустимой точки 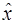 выполнены условия а), б), в) и выполнено условие Слейтера (т.е.
выполнены условия а), б), в) и выполнено условие Слейтера (т.е. 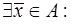
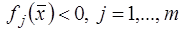 ), то
), то 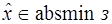 . ■
. ■
Теорема Куна-Таккера дает необходимые и достаточные условия абсолютного минимума в задаче выпуклого программирования.
Замечание. Если в выпуклой задаче (1) отсутствует ограничение в виде включения 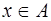 , (т.е.
, (т.е. 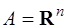 ), то условие а) теоремы Куна-Таккера равносильно условию стационарности функции Лагранжа
), то условие а) теоремы Куна-Таккера равносильно условию стационарности функции Лагранжа 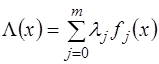 :
: 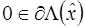 . Это следует из того, что функция Лагранжа
. Это следует из того, что функция Лагранжа 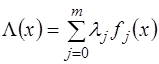 с неотрицательными множителями Лагранжа является выпуклой функцией. А по аналогу теоремы Ферма для выпуклых функций условие
с неотрицательными множителями Лагранжа является выпуклой функцией. А по аналогу теоремы Ферма для выпуклых функций условие 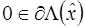 является необходимым и достаточным условием абсолютного минимума функции Лагранжа в точке
является необходимым и достаточным условием абсолютного минимума функции Лагранжа в точке 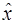 .
.
Задача. Найти расстояние от точки 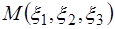 до конуса
до конуса 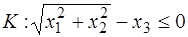 .
.
Решение. Формализуем поставленную задачу, взяв в качестве целевой функции квадрат расстояния от точки 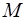 до точки, принадлежащей конусу:
до точки, принадлежащей конусу:
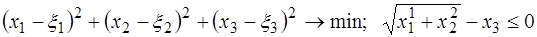 .
.
Составим функцию Лагранжа
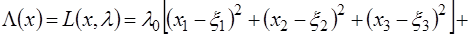
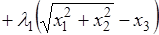 .
.
Выпишем необходимые условия абсолютного минимума:
а) 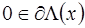 ,
,
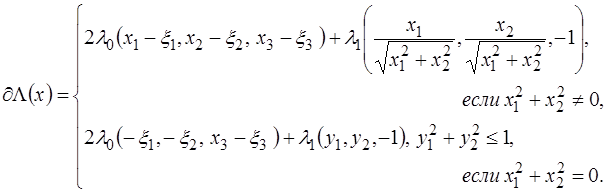
б)  ;
;
в) 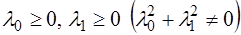 .
.
Если  , то из условия а) получим
, то из условия а) получим  , т.е. вектор множителей Лагранжа равен нулю, поэтому этот случай не подходит.
, т.е. вектор множителей Лагранжа равен нулю, поэтому этот случай не подходит.
Положим  . Разберем отдельно два случая:
. Разберем отдельно два случая: 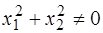 и
и 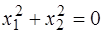 .
.
I. 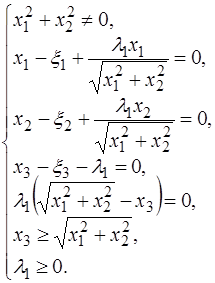
Рассмотрим два варианта выполнения условия дополняющей нежесткости.
Iа) 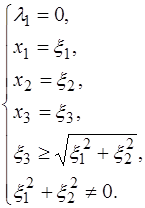
Следовательно, если  , то
, то
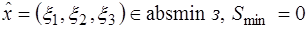 .
.
Iб) 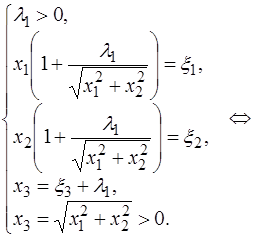
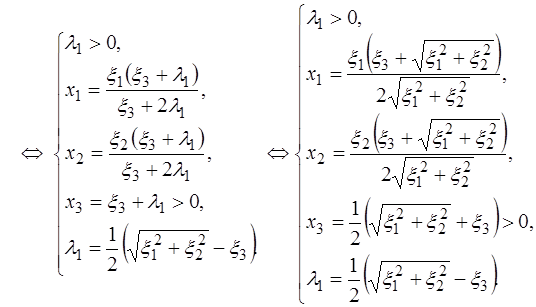
Следовательно, если  , то
, то
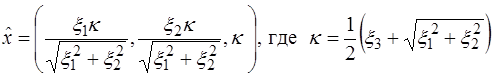 ,
,
 . Тогда расстояние от точки
. Тогда расстояние от точки 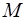 до конуса
до конуса 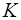 равно
равно
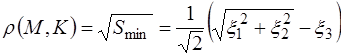 .
.
II. 
IIа) 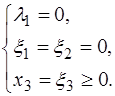
 если
если  , то
, то
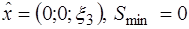 .
.
IIб) 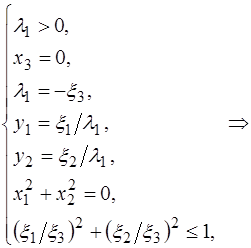 если
если 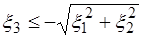 , то
, то
 ,
,  .
.
Ответ: Если  , то
, то
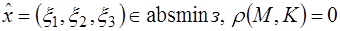 .
.
Если  , то
, то
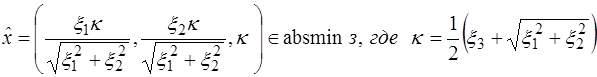 ,
,
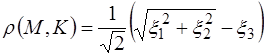 .
.
Если 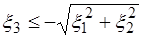 , то
, то 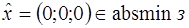 ,
,
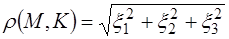 . ●
. ●