Некоторые сведения из теории статистических решений

 

Рассмотрим основные результаты теории статистических решений на следующем примере. Пусть совокупность объектов подразделена на классы Ω₁ и Ω₂, а для характеристики объектов используется признак х [15]. Известны описания классов — условные плотности распределения вероятностей f₁ (х) и f₂ (х) значений признака объектов классов Ω₁ и Ω₂, а также априорные вероятности P(Ω₁) и Р(Ω₂) появления объектов. В результате эксперимента определено значение признака х₀⁰ распознаваемого объекта (рис. 4.1).

Чтобы определить, к какому классу отнести объект, обозначим х₀ некоторое, пока неопределенное значение признака х и условимся о следующем правиле принятия решений: если измеренное значение признака у распознаваемого объекта х⁰>х₀, то объект будем относить к классу Ω₂, если х⁰£х₀,— к классу Ω₁ Если объект относится к классу Ω₁ а его считают объектом класса Ω₂, то совершена ошибка — ошибка первого рода, условная вероятность которой

 

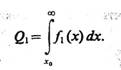
(4.1)

 

По терминологии теории статистических решений, ошибочно выбрана гипотеза Н₂, в то время как справедлива гипотеза Н_1. Наоборот, если справедлива гипотеза Н₂, а отдано предпочтение гипотезе Н_х, то совершена ошибка второго рода, условная вероятность которой

 

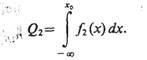
(4.2)

 

По терминологии теории статистических решений, ошибочно выбрана гипотеза Н₁ в то время как справедлива гипотеза Н₂.

В некоторых приложениях теории статистических решений вероятность ошибки первого рода называют вероятностью ложной тревоги, а вероятность ошибки второго рода — вероятностью пропуска цели.

Пусть значения признака х у объекта в каждом классе подчинены нормальным законам распределения с математическими ожиданиями m₁ и m₂ и среднеквадратичными отклонениями s₁ и s₂, соответственно:

 

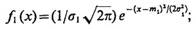
(4.3)

(4.4)

 

Если в (4.1) подставить (4.3), то условная вероятность ошибки первого рода

 

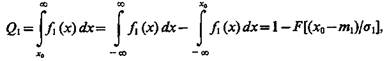
(4.5)

 

где 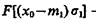— функция Лапласа.

 

 

Рис. 4.1

 

Если в (4.1) подставить (4.4), то условная вероятность ошибки второго рода

 

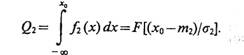
(4.6)

 

Условные вероятности правильных решений при справедливости гипотез Н₁ и Н₂, соответственно

 

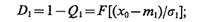
(4.7)

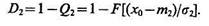
(4.8)

 

В теории статистических решений D₁ — размер испытаний, a D₂ = 1 — Q₂ — мощность испытаний.

В (4.5) и (4.6) при интегрировании функций f₁(х) и f₂(х) в пределах — ¥ — х₀ произведена замена (х₀-m)/s на t, которая приводит к интегралам вида

 

 

Для вычисления этих интегралов, поскольку они не выражаются через элементарные функции, пользуются таблицами специальных функций [16]:

 

(4.9)

 

Соображения, которыми следует руководствоваться при выборе значения признака х₀ (при разделении пространства признака х на два полупространства: R₁ и R₂), должны учитывать потери, сопряженные с правильными и ошибочными решениями. Функции потерь, характеризующие потери при совершении ошибок первого и второго рода, а также потери правильных решений, образуют в данном случае платежную матрицу вида

 

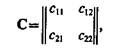
(4.10)

 

где с₁₁ и с₂₂, с₁₂ и с₂₁ — потери, связанные соответственно с правильными решениями и ошибками первого и второго рода.

Средний риск при многократном распознавании неизвестных объектов равен сумме потерь, связанных с неправильными и правильными решениями, с учетом вероятностей их появления и априорных вероятностей поступления на вход системы распознавания объектов классов Ω₁ и Ω₂.

 

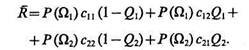
(4.11)

 

Подставив в (4.11) выражения (4.1) и (4.2), получим

 

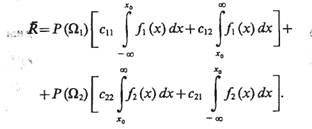
(4.12)

 

Системы распознавания — системы многократного действия. Поэтому необходимо, чтобы выбор значения х₀ был осуществлен с учетом того, что Rã минимален. Для определения значения х₀, при котором средний риск минимален, продифференцируем Rã по х и приравняем производную нулю, положив х=х₀:

 

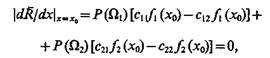
(4.13)

 

откуда

 

(4.14)

 

Отношение условных плотностей распределения f₂(x)/f₁(x) = l(х) называют коэффициентом правдоподобия или отношением правдоподобия. Правая часть (4.14)

 

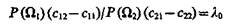
(4.15)

определяет собой пороговое (критическое) значение коэффициента правдоподобия.

Определим значение х₀ при условии, что значения признака х у объектов, относящихся к классам Ω₁ и Ω₂, подчинены нормальным законам распределения N₁ (x, m₁ s₁) и N₂ (x, m₂, s₂) соответственно. Для этого подставим в (4.14) значения f₁(x) и f₂(х), определяемые (4.3) и (4.4), т. е. 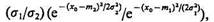откуда

 

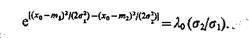
(4.16)

 

Решая (4.16) относительно х₀, получим

 

 

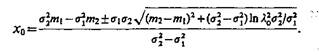
(4.17)

 

В частном случае, когда s₁ = s₂ = s, из (4.16) находим

 

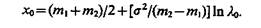
(4.18)

 

И если c₁₁=с₂₂ = 0, c₁₂ = c₂₁ и P(Ω_l) = P(Ω₂), то

 

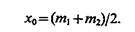
(4.19)

 

Значение х₀ позволяет оптимальным образом (в смысле минимума среднего риска) разделить признаковое пространство на области R₁ и R₂. Область R₁ состоит из х£х₀, для которых l(х) £l₀, а область R₂ — из х > х₀, для которых l(х) > l₀. Поэтому решение об отнесении объекта к классу Ω следует принимать, если значение коэффициента правдоподобия меньше его критического значения, а решение об отнесении объекта к классу Ω₂ — при противоположной ситуации. В общем случае, когда число классов m > 2, а объекты описываются набором признаков x₁, ..., x_N или вектором х={х₁ ..., х_N}, отношение правдоподобия между классами Ω_k и Ω_l будет x_kl=f_k(x)/f_l(x), k, l=1, ..., m, платежная матрица имеет вид (1.7), а величина Rã=

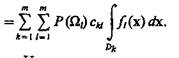
Из условия минимума значения среднего риска уравнение границы в многомерном пространстве признаков между областями Dk и Di, соответствующими классам Ω_k и Ω_l, будет

 

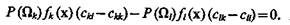
(4.20)

 

Если полагать с_kk=с_ll=0, a c_kl=c_lk=l, то

 

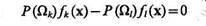
(4.21)

 

или

 

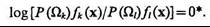
*3десь и в § 4.6 log=log;.

(4.22)

 

Пусть f_i(х) = ехр[0,5(х-m_i)^TK^i-1(х-m_i)]/[(2π)^1/2K_i^1/2], i=l, .... m,— функция плотности многомерного нормального закона распределения со средним вектором m_i, и ковариационной матрицей К_i.

Тогда уравнение границы

 

*3десь и в § 4.6 log=log;.

(4.23)

 

Если K_k=K_l=K, то

 

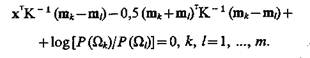
(4.24)

 

Уравнение (4.24) — уравнение гиперплоскости, разделяющей с точки зрения минимальных средств потерь наилучшим образом многомерное признаковое пространство на области, соответствующие классам Ω_k и Ω_l, k, 1=1, ..., m.