Минимаксный критерий

 

При построении систем распознавания возможны такие ситуации, когда априорные вероятности появления объектов соответствующих классов неизвестны. Минимизировать значение среднего риска принятия решений на основе байесовской стратегии в этом случае не представляется возможным. Применительно к этой ситуации рационально использовать критерий, который минимизирует максимально возможное значение среднего риска. Этот критерий называют минимаксным критерием.

Минимаксная стратегия состоит в том, что решение о принадлежности неизвестного объекта соответствующему классу принимается на основе байесовской стратегии, соответствующей такому значению P(Ω₁), при котором средний риск максимален. Покажем преимущество минимаксной стратегии по сравнению с другими возможными стратегиями в условиях, когда неизвестны значения Р(Ω_i), i=1, ..., m.

При наличии классов Ω₁ и Ω₂ байесовский риск с учетом того, что P(Ω₂) = 1 —P(Ω₁), c₁₁ = c₂₂ = 0, a c₁₂ = c₁ и с₂₁ = с₂, равен

 

(4.36)

 

Построим график функции Rã_min =f[Р (Ω₁)], помня при этом, что при P(Ω₁) = 0 и P(Ω₁)=l Rã_min = 0 (рис. 4.3).

Пусть Rã_min достигает своего наибольшего значения при P(Ω_l)=P¢(Ω₁). Этот риск представляет собой максимальное значение минимального байесовского риска (обозначим его Rã_min^max). Применение минимаксного критерия означает, что при отсутствии данных относительно априорных вероятностей появления объектов следует ориентироваться на P(Ω_l)=P¢(Ω₁).

Средние потери при P(Ω_l)=P¢(Ω₁)определяются касательной к кривой Rã=f[P(Ω_l)] в точке, соответствующей P¢(Ω₁):

 

(4.37)

 

где Q¢₁ = Q₁ [Р¢ (Ω₁)] и Q¢₂ = Q₂ [P^¢ (Ω₁)] — ошибки первого и второго рода при априорной вероятности P(Ω_l)=P¢(Ω₁).

Так как при P¢(Ω₁) средние потери достигают максимума, то касательная, определяемая (4.37), параллельна оси абсцисс и значит средние потери неизменны в условиях, когда действительное значение P(Ω₁) отличается от выбранного значения P¢(Ω₁).

Минимаксная стратегия обеспечивает то, что при P(Ω₁)< P¢(Ω₁) и P(Ω₁)> P¢(Ω₁). средние потери не будут превышать максимального значения минимальных средних (байесовских) потерь.

Рассмотрим, к каким результатам приводит выбор другого значения P(Ω₁)., отличного от P¢(Ω₁).. Положим, что выбрано значение P²(Ω₁).. Средние потери в этом случае описываются уравнением касательной к кривой Rã=f[P(Ω₁)] в точке А:

 

(4.38)

 

где 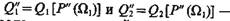- ошибки первого и второго рода при априорной вероятности P(Ω₁)=P²(Ω₁).

Так как байесовская стратегия обеспечивает минимальный средний риск, то кривая, определяемая (4.36), лежит ниже прямой для всех значений P(Ω₁)¹P²(Ω₁).

Рассматриваемая стратегия приводит к следующему. Положим, сделано предположение, что априорная вероятность равна P²(Ω₁). Тогда если априорная вероятность на интервале 0 — P²¢(Ω₁).отлична от P²(Ω₁)., то средний риск будет меньше, чем при минимаксной стратегии. Но если P(Ω₁)> P²(Ω₁)., то потери

 

 

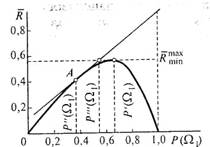
Рис. 4.3

 

Рис. 4.4

 

возрастают, достигая чрезмерных значений. Выбор минимаксной стратегии гарантирует от подобных потерь.

Для определения алгоритма принятия решения, соответствующего минимаксной стратегии, продифференцируем (4.36) по Р(Ω₁) и приравняем производную нулю. В результате получим

 

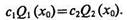
(4.39)

 

Это соотношение, представляющее собой равенство условных значений средних рисков при ошибках первого и второго рода, позволяет определить х₀ и построить следующий алгоритм классификации: если измеренное значение признака х у объекта w равно х⁰, то wÎΩ₁ если х=х⁰£х₀, и wÎΩ₂, если х=х⁰>х₀.

Минимаксная стратегия, предлагающая значение P(Ω₁) полагать равным P¢(Ω₁), приводит к следующему пороговому значению коэффициента правдоподобия:

 

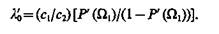
(4.40)

 

Определение l¢₀ позволяет записать алгоритм классификации так: wÎΩ₁ если l(x)£l¢₀, и wÎΩ₂ если l(х)> l¢₀.

Если с₁ = с₂ то, как следует из (4.38), минимаксная стратегия приводит к равенству условных вероятностей ошибок первого и второго рода.

В заключение заметим, что минимаксная стратегия есть байесовская стратегия для наихудших значений априорных вероятностей, дающая хотя и осторожное, но гарантированное значение среднего риска.