Изображающие числа и базис

 

Булева функция считается заданной, если можно указать значения истинности этой функции при всех возможных комбинациях значений истинности входящих в нее элементов. Таблицу, которая представляет все возможные комбинации значений истинности некоторого набора элементов А, В, С, ..., называют базисом. Если значение «истина» обозначить 1, а значение «ложь» — 0, то для одного элемента А базис содержит 2¹ колонок:

 

 

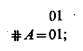
для двух элементов А, В — 2² колонок:

 

 

для трех элементов А, В, С — 2³ колонок:

 

 

и вообще для n элементов А₁ ..., А_n базис содержит и строк и 2 колонок. Если колонки базиса рассматривать как целые двоичные числа, записанные так, что самый младший разряд их соответствует первой строке базиса, а самый старший — последней строке, то колонки базиса для n элементов представляют собой числа от 0 до 2ⁿ— 1. Будем считать эти числа номерами колонок базиса и отметим сверху каждую колонку ее номером. Если колонки базиса упорядочены и записаны в возрастающем порядке их номеров слева направо, то базис будет стандартным, все другие базисы — нестандартные. Для n элементов существует столько базисов, сколько можно составить перестановок из 2ⁿ колонок, т. е. (2ⁿ)! Стандартный базис для элементов А, В, С, ... обозначается b [А, В, С, ...], причем порядок элементов в квадратных скобках совпадает с порядком строк базиса.

Строки базиса называют изображающими числами соответствующих элементов и обозначают приписыванием слева от элемента знака #. Заметим, что по отношению к стандартному базису b[А, В, С, В] изображающее число ФА состоит из чередующихся нулей и единиц, #В — из пар нулей и пар единиц, # С — из четверок нулей и четверок единиц и т. д., т. е. #D = 0000 0000 1111 1111.

Используя базис, можно явным образом перечислить все значения истинности булевой функции при всех возможных комбинациях значений истинности элементов, от которых она зависит. Для этого необходимо ввести некоторые операции над изображающими числами элементов, соответствующие операциям над высказываниями.

Изображающее число дизъюнкции двух элементов равно сумме изображающих чисел слагаемых:

 

(6.2)

 

причем сложение #А и #В выполняется поразрядно без переносов в высшие разряды по правилу 0 + 0 = 0,0+1 = 1+0= 1,1 + 1 = 1. Например, по отношению к базису b [А, В, С] изображающее число #(А + В + С)=#(А+В)+#С=#А+#В+#С= = 0101 0101+0011 0011+0000 1111=0111 1111.

Изображающее число конъюнкции двух элементов определяется как произведение изображающих чисел сомножителей:

 

(6.3)

 

причем перемножение #А и #В выполняется поразрядно по правилу 00 = 0, 01 = 10 = 0, 11 = 1. Например, по отношению к b[А, В, С]

 

 

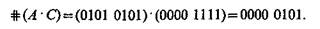
Изображающее число отрицания `А получается из изображающего числа А заменой в каждом разряде 0 на 1 и 1 на 0, например

 

(6.4)

 

Отметим двойной смысл символов « + » и «×» в логических формулах и операциях над изображающими числами. В одном случае эти символы используются для обозначения дизъюнкции и конъюнкции над высказываниями, а в другом случае — для операций поразрядного логического сложения и умножения изображающих чисел элементов. Руководствуясь правилами (6.2) — (6.4), можно найти изображающее число любой булевой функции. Например, по отношению к базису b [А, В, С, D] изображающее число #(А×В+`В×`С×D) = (010l 0101 0101 0101)´ (0011 0011 0011 0011) + (1100 1100 1100 1100)(1111 0000 1111 0000) ´ (0000 0000 1111 1111) = 0001 0001 0001 0001+0000 0000 1100 0000 = 0001 0001 1101 0001. Следовательно, данная функция истинна только при таких комбинациях значений истинности элементов А, В, С, D, которые соответствуют 3, 7, 8, 9, 11 и 15-му столбцам базиса.

Укажем, что #I = 1111, ..., т. е. имеет единицы во всех разрядах #0 = 0000..., т. е. имеет 0 во всех разрядах, #Х= # У тогда и только тогда, когда Х= Y; Х®Y тогда и только тогда, когда #Y имеет 1, по крайней мере, в тех разрядах, в которых #Х содержит 1.

Используя изображающие числа, можно доказать любое из правил 1 — 20 алгебры логики.

Докажем, например, соотношение A×B+`B×`C×D = A×B+`B´`C×D+A×`C×D, вытекающее из правила 19. Изображающее число левой части было сосчитано в предыдущем примере и равно 0001 0001 1101 0001. Изображающее число правой части отличается от этого числа только на #А×`С×D = (0101 0101 0101 0101) (1111 0000 1111 0000) (0000 0000 11111111) = = 0000 0000 0101 0000. Поразрядное логическое сложение число #А×`С×D с числом 0001 0001 1101 0001 не изменяет последнего. Следовательно, изображающие числа левой и правой частей рассматриваемого соотношения тождественны.

Чтобы проверить истинность импликации (А×В+В×`С)®(А + С), достаточно по отношению к b [А, В, С] вычислить #(А×В+`В ×C) = (010l 0101)×(0011 0011) + (1100 1100)×(0000 1111) = 0001 0001+0000 1100 = 0001 1101 и #(A + С)=0101 0101 + +0000 1111=0101 1111 и убедиться, что в разрядах 3, 4, 5, 7 последнего числа стоят единицы.