Зависимость и независимость высказываний
Условия независимости. Поскольку каждая булева функция может иметь два значения истинности, n булевых функций могут образовывать 2n комбинаций значений истинности. По определению, n булевых функций f1(А, В, С, ...), ..., fn(А, В, С, ...) независимы, если в совокупности при всех возможных значениях аргументов А, В, С, ... они могут принимать 2n комбинаций значений истинности. Следовательно, для проверки независимости функций f1(A, В, С, ...), ...,fn(А, В, С, ...) необходимо по отношению к базису b[А, В, С, ...] вычислить их изображающие числа
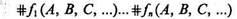
(6.5)
и проверить, образуют ли столбцы набора (6.5) 2n чисел 0, 1, ..., 2 n —1; если 2n чисел имеется, то функции независимы, в противном случае — зависимы. При этом считается, что, как во всяком базисе, разряды двоичных чисел, представленных столбцами набора (6.5), возрастают вдоль столбца сверху вниз.
Пример. Установить, зависимы или независимы функции А×В+`А×`В и `B. Запишем их изображающие числа в последовательные строки:
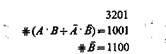
Колонки набора представляют все возможные комбинации значений истинности, соответствующие числам 0, 1, 2, 3. Следовательно, рассматриваемые функции независимы.
Пример. Установить, зависимы или независимы функции А×В+`А×В, `В и А×`В+`А×В.
Эти функции зависимы, так как в колонках набора
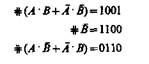
содержатся числа 1, 3, 4, 6, а числа 0, 2, 5, 7 отсутствуют.
Метод нахождения явного вида логической зависимости. Чтобы найти явную форму логической связи зависимых булевых функций f1(Л, В, С, ...), ...,fn(A, В, С, ...) в виде
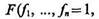
(6.6)
поступают следующим образом. В базисе b[А, В, С] выписывают в последовательные строки изображающие числа #f1, ..., #fn и определяют, какие числа отсутствуют в наборе столбцов (6.5), повторяющиеся значения чисел считают один раз. Столбцы набора (6.5) представляют собой комбинации значений истинности функций f1 ...,fn, при которых соответствующие элементарные произведения, составленные из f1 ...,fn, истинны. Так как #(F= 1)= # F, то, следовательно, имеющиеся в наборе (6.5) столбцы указывают номера тех колонок базиса b[f1 ...,fn], совпадающие с номерами разрядов #F(f1 ...,fn), на которых функция F истинна, т. е. в соответствующих разрядах изображающего числа #F(f1 ...,fn) должны стоять единицы.
Таким образом, изображающее число функции F(f1 ...,fn), отвечающей связи (6.6), получим, если в его разрядах относительно базиса b(f1 ...,fn), которые имеют номера отсутствующих в наборе (6.5) столбцов, поставим 0, а в остальных разрядах — 1.
Пример. Требуется установить явный вид логической зависимости функций 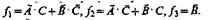
Вычислим по отношению к базису b[А, В, С]:
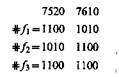
Выпишем последовательно все столбцы в этом наборе изображающих чисел как строки или соответствующие двоичные числа и укажем справа их десятичные значения: 111=7, 101 = 5, 010=2, 000 = 0, 111=7, 110=6, 001 = 1, 000 = 0.
Видим, что имеются только числа 0, 1, 2, 5, 6 и 7, а числа 3, 4 отсутствуют. Это означает, что по отношению к b[f1, f2, f3] изображающее число связи F(f1, f2, f3) = 1 имеет вид #F( f1, f2, f3)= 1110 0111.
Так как 1110 0111 = #[(f1 +f2)×f3 + (f1+f2)×f3], то функции f1, f2, f3 связаны соотношением (f1 +f2)×f3 + (f1+f2)×f3 = 1.
В справедливости последнего равенства можно убедиться непосредственно, если подставить в него выражения для f1, f2, f3, записанные как функции от А, В, С. Выполним эту подстановку через изображающие числа f1, f2, f3 по отношению к b[А, В, С]: