Булевы уравнения
Решение многих задач, связанных с распознаванием объектов, может быть сведено к нахождению решений булевых алгебраических уравнений с одним (или более) неизвестным. Примером булева уравнения с одним неизвестным может служить соотношение Х×(А + В) — А × В× С, где X — некоторая булева функция, зависящая от А, В, С, которую требуется найти, так чтобы в результате подстановки Х(А, В, С) в данное уравнение оно обращалось в тавтологию.
Перейдем от элементов X, А, В, С к их изображающим числам. Относительно базиса b [А, В, С] найдем #А×В×С= 0000 0001; # (А + В) = 0111 0111 и, следовательно, #Х должно быть таким, чтобы выполнялось равенство (0111 0111) ´ (#X) = 0000 0001, откуда #Х= ´ 000´001, где вместо ´ можно написать как 0, так и 1.
Таким образом, рассматриваемое уравнение имеет четыре решения, соответствующие изображающим числам 0000 0001,

Аналогично можно найти решение уравнения в виде импликации, например

(6.7)
Так как #(А + В+`С) = 1111 0111, #(А×В+`B×C) = 0001 1101, то #Х=000´ ´´0´.
Таким обоазом. имеется 24=16 решений уравнения (6.7): 0, 
Уравнение в виде импликации всегда можно записать как соотношение эквивалентности, например, вместо (6.7) можно было бы написать  или после упрощения
или после упрощения 
Существуют также уравнения, которые вообще не имеют решений, например 
Решение булевых уравнений. Изложим общий метод решения булевых уравнений, основанный на вычислении изображающих чисел неизвестных, на примере уравнения, записанного в форме эквивалентности, которое возникает из рассмотрения следующей задачи.
Когда было много разговоров о существовании «летающих тарелок» в связи с утверждениями некоторых лиц о том, что ночью ими наблюдались странные небесные тела, был произведен опрос населения двух близлежащих к месту предполагаемого появления этих тел населенных пунктов.
Систематизация результатов опроса жителей первого населенного пункта показала следующее: а) в небе появились сгустки слабо светящейся ионизированной пыли (А), б) среди атмосферных облаков (В) появилось одиночное светлое дискообразное тело радиусом приблизительно 100 м (X) и больше не было никаких других тел (`Y), в) далеко в небе показалась группа движущихся сигарообразных тел (Y), и движение этих тел сопровождалось слабыми мерцающими разрядами атмосферного электричества (С).
Ответы жителей второго населенного пункта можно было объединить в такие группы: а) не было ни светящейся ионизированной пыли (`А), ни большого светлого дискообразного тела (`X), ни сигарообразных тел (`Y), б) не видели ни атмосферных облаков (`В), ни светлого дискообразного тела (`X), в) наблюдались слабые разряды атмосферного электричества (С), г) среди облаков (В) были видны сгустки слабо светящейся ионизированной пыли (А). На основании этих данных требовалось определить, следует ли принимать всерьез заявления некоторых лиц о наблюдавшихся ими странных небесных телах X и У или же представления о телах X и Y могли быть вызваны комбинированными действиями атмосферных явлений А, В, С. Используя введенные обозначения, результаты опроса представим в виде следующего булева уравнения:

(6.8)
Решение вопроса о существовании тел X и Y сводится к определению возможности разрешить уравнение (6.8) относительно неизвестных X и Y и выразить их как функции от элементов А, В, С. Если решение Х(А, В, С), Y(A, В, С) существует и, кроме того,
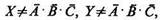
(6.9)
то нет оснований делать вывод о появлении каких-либо тел X, Y. Если же решения, отличного от (6.9), не существует, то следует отнестись к заявлениям «очевидцев» с большой серьезностью.
Вычисление #X и # Y относительно базиса b [А, В, С] удобно проводить с помощью следующей рабочей таблицы [29]:
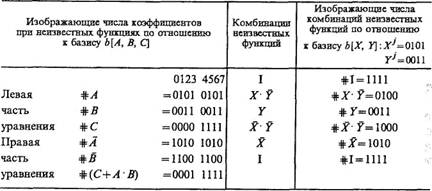
Рекомендуется следующий порядок работы при вычислении #X и #Y относительно b[А, В, С]. Возьмем первую пару значений (Xj, Yj) при j=0, т. е. (Х0, Y0) = (0,0), которые соответствуют нулевому столбцу базиса b[X, Y]. Паре значений (Х0, Y0) = (0, 0) отвечают колонка  в наборе изображающих чисел элементов I, X×`Y и Y для левой части уравнения (6.8) и колонка
в наборе изображающих чисел элементов I, X×`Y и Y для левой части уравнения (6.8) и колонка  в наборе изображающих чисел
в наборе изображающих чисел  и I для правой части этого уравнения. Колонку
и I для правой части этого уравнения. Колонку  умножаем на нулевую колонку в наборе изображающих чисел коэффициентов А, В и С для левой части уравнения и результат суммируем по правилу логического сложения: 01 + 00 + 00 = 0.
умножаем на нулевую колонку в наборе изображающих чисел коэффициентов А, В и С для левой части уравнения и результат суммируем по правилу логического сложения: 01 + 00 + 00 = 0.
Аналогично поступим с колонкой  и нулевой колонкой
и нулевой колонкой  в наборе
в наборе  для правой части уравнения: 1×1 + 1×1 + 0×1 = 1.
для правой части уравнения: 1×1 + 1×1 + 0×1 = 1.
Так как полученные результаты не совпадают, то, следовательно, пара значений (Х0, Y0) = (0, 0) в разрядах i=0 изображающих чисел #Х и #Y, вычисленных относительно базиса b[А, В, С], не удовлетворяет (6.8) и потому должна быть отброшена.
Далее проверяется пара значений (Xj, Yj)=(1,0) при j= 1 в разрядах с номером i=0 изображающих чисел #X и # Y по отношению к b [А, В, С]. Как и раньше, необходимо сравнить логическую сумму произведения колонки на колонку
на колонку т. е. 0×1 + 0×1 ++ 0×0 = 0, с аналогичным результатом для колонок
т. е. 0×1 + 0×1 ++ 0×0 = 0, с аналогичным результатом для колонок и
и 0×1 + 0×1 + 1×0 = 0.
0×1 + 0×1 + 1×0 = 0.
 — колонка с номером j= 1 в наборе
— колонка с номером j= 1 в наборе  и # Y, а
и # Y, а —колонка с номером i=0 в наборе #A, #B #С. Аналогично,
—колонка с номером i=0 в наборе #A, #B #С. Аналогично,  — колонка с номером j= 1 в наборе
— колонка с номером j= 1 в наборе и # I, a
и # I, a — колонка с номером i= 1 в наборе
— колонка с номером i= 1 в наборе  и #(C=A×B)
и #(C=A×B)
Поскольку суммы произведений колонок совпадают, можем записать в нулевые (i=0) разряды #X и #Y по отношению к b[А, В, С] значения Х1 = 1, Y1 = 0, как показано в таблице результатов:

При проверке всех оставшихся пар значений (Xj, Yj) для разрядов изображающих чисел #X и # Y с номером 1 = 0 в базисе b [А, В, С] отбросим пару (X2, У2) = (0,1), поскольку 1×0 + 0×0 + 1×0¹0×1 + 1×1 + 1×0, и запишем в разряд i=0 таблицы результатов (Х3 ,У3) = (1,1), так как 1×0 + 0×0+1×0 = 0×1 +1×0 + 1×0.
Аналогично можно выбрать все допустимые пары значений (Xj, Yj) по отношению к разрядам 1,2 и т д. изображающих чисел #Xи #Y в базисе b[А, В, С].
В общем случае для проверки j-й пары значений (Xj, Yj) колонки, стоящие справа от неизвестных, последовательно умножаются на i-ю колонку коэффициентов и результат логически складывается, при совпадении значений сумм выше и ниже средней горизонтальной черты рабочей таблицы, разделяющей наборы чисел для правой и левой частей уравнения, соответствующие j-й колонке неизвестные значения {Xj, Yj) подставляются в j-й разряд таблицы результатов.
Поступая аналогично, получим решение для #X и # Y, приведенное в таблице результатов. Согласно этой таблице, имеются 2×2×2×4×2×4×3×4 = 3072 различных неэквивалентных пар решений уравнения (6.8). Например, если, в частности, взять числа, стоящие первыми в каждом разряде (i=0, 1, ..., 7) таблицы результатов, то получим: 
 т. е. представление о существовании тела X либо не связано ни с одним из названных атмосферных явлений, либо вызвано только появлением облаков и атмосферными разрядами электричества, а представление о существовании группы тел Y вызвано либо одними облаками, либо одними атмосферными разрядами. Поэтому нет серьезных оснований считать, что небесные тела X я Y действительно существуют.
т. е. представление о существовании тела X либо не связано ни с одним из названных атмосферных явлений, либо вызвано только появлением облаков и атмосферными разрядами электричества, а представление о существовании группы тел Y вызвано либо одними облаками, либо одними атмосферными разрядами. Поэтому нет серьезных оснований считать, что небесные тела X я Y действительно существуют.
Изложенный метод может быть применен и при решении системы уравнений в форме эквивалентности с тем, однако, усложнением, что проверяемая пара значений (Xj, Yj) должна одновременно удовлетворять всем уравнениям системы.
Процедуру отбора пар значений (Xj, Yj), удовлетворяющих, например, уравнению (6.8), можно значительно упростить, если ввести в рассмотрение операции над булевыми матрицами. Прямоугольная матрица называется булевой, если элементы ее — числа 0 и 1. Произведение булевых матриц

(6.10)
определяется по правилам обыкновенного матричного умножения, т. е.  с той только разницей, что операция суммирования произведений элементов строк и столбцов заменяется логическим сложением, например
с той только разницей, что операция суммирования произведений элементов строк и столбцов заменяется логическим сложением, например

Соотношение импликации, обозначаемое ||аij||®||bij||, справедливо для двух булевых матриц: ||аij|| и ||bij||, если нет i и j таких, что bij =0 и aij = 1, например

Транспонированной матрицей по отношению к ||аij||называют Матрицу

получаемую из матрицы ||аij|| при перемене местами строк и столбцов.
Последовательное умножение с последующим сложением каждого столбца в наборе изображающих чисел коэффициентов на все столбцы набора изображающих чисел неизвестных эквивалентно умножению булевой матрицы, полученной транспонированием таблицы изображающих чисел коэффициентов, на булеву матрицу, составленную из изображающих чисел неизвестных. Выполняя эти вычисления для левой части уравнения (6.8), найдем булеву матрицу:

(6.11)
Аналогично для правой части уравнения (6.8) находим

(6.12)
Сравнение матриц ||cij|| и ||dij|| показывает, что в строках i=0 совпадают элементы с индексами j = 1 и j = 3, т. е. c01 = d01 = 0, c03 = d03 = 0, и следовательно, в разряд i=0 таблицы результатов' должны быть внесены значения {X1, Y1) = (1,0) и {Х3, У3) = (1,1).
В строках i= 1 совпадают элементы с индексами j = 0 и j = 2, т. е. c10 = d10 1 и c12 = d12 =1, поэтому в разряд i=1 таблицы результатов записываются значения (Х0, Y0) = (0,0) и (X2, У2) = (0,1). Точно так же получим для всех оставшихся i следующие совокупности значений индекса.j: i=2,j=2,3; i=3,j=0, 1, 2, 3; i=4,j=2,3; i=5,j=0, 1, 2, 3; i=6,j=1, 2, 3; i=7,j=0, 1, 2, 3; они полностью соответствуют выписанной ранее таблице результатов.
Для системы из r уравнений в форме эквивалентности, которые будем предполагать перенумерованными с помощью индекса s, решения находятся из условия совпадения элементов одновременно во всех r матрицах ||csij|| и ||dsij||, s=1, ..., r, вычисленных таким же образом, как и матрицы (6.11) и (6.12). Если при каком-либо / не существует таких Y, что csij= dsij, s=l, ..., r, то система уравнений не имеет решения.
Для уравнений в форме импликации не нужно требовать совпадения элементов матриц ||cij|| и ||dij||; для существования решения достаточно только, чтобы единице слева обязательно соответствовала единица справа.