Частные подходы к принятию решений при распознавании

Решение задачи оптимизации распознавания в рассмотренной постановке требует наличия определенных данных. Когда они отсутствуют, приходится пользоваться частными подходами к принятию решений. Остановимся на некоторых из них.

Критерий заданного превышения максимальной вероятности по отношению ко всем остальным. Положим, что в результате проведения экспериментов у объекта w определены значения v-признаков x₁ = x⁰₁, ..., х_v=х⁰_v и установлены условные апостериорные вероятности отнесения его к классам Ω_i, i= 1, ..., m, т. е. величины Р(Ω_i |а_v), где a_v = {x_l= x⁰₁, x₂= x⁰₂, ..., х_v= x⁰_v}. Решение о принадлежности этого объекта к тому или другому классу в соответствии с рассматриваемым критерием производится на основании соотношения

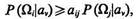
(9.18)

где a_ij — некоторые числа для какого-либо фиксированного класса i при всех j¹i, j= 1, .., m.

При выполнении условия (9.18) принимается гипотеза H_i которая означает утверждение — объект принадлежит классу Ω_i. Величины а_ij связаны с вероятностями ошибочного решения следующим образом. Обозначим b_ij вероятность принять гипотезу H_j, в то время как справедлива гипотеза H_i.

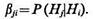
(9.19)

Тогда вероятность a_i отклонить гипотезу H_i в то время как она справедлива, равна

(9.20)

Так как в соответствии с принятым критерием вероятность не совершить ошибку при принятии гипотезы H_i должна быть в а_ij раз больше вероятности совершить ошибку при том же условии о принятии гипотезы H_i то

(9.21)

Пусть для каждого f-го класса значения вероятностей b_ij, ошибочных решений равны между собой, т. e. тогда

Если, кроме того, предположить, ч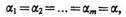то то , где m — число классов, для которых Следовательно,

Пусть тогда если a₀ — выбранное значение вероятности ошибочного решения, то в соответствии с (9.19) гипотеза H_i принимается, когда неравенство

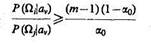
(9.22)

выполняется для всех j¹i, 1£i, j£m. В противном случае необходимо учитывать (v+ 1)-й признак, поскольку при v-признаках не обеспечивается уровень (1 —a₀) доверительной вероятности. Например, если вероятность ошибки принять равной a₀ = 0,05, то для двух гипотез вероятность отнести объект к одному классу должна быть в 19 раз больше вероятности отнести объект к другому классу. Для трех классов наибольшее значение вероятности P(Ω_i|a_v) должно быть в 38 раз больше всех других вероятностей P(Ω_i|a_v) j¹i, и т. д.

Значение ошибочного решения a₀ может быть выбрано из следующих соображений. Пусть при использовании v-признаков получено r исключающих друг друга гипотез Н_j, j=1, 2, ..., r. Предположим, что С, — стоимость ошибки при принятии гипотезы Н_j и при правильном ответе плата не производится. Тогда математическое ожидание платы за одно решение

(9.23)

где P(Ω_i|a_v) — вероятность гипотезы Н_j, a_j — соответствующая вероятность ошибки.

Обозначим С^v⁺¹ стоимость определения (v+l)-ro признака, а Р* — вероятность того, что на (v— 1)-м шаге процесс закончится принятием определенного решения (например, однозначного решения). Тогда после проведения (v — 1)-го эксперимента средняя плата за ошибки, включая стоимость этого эксперимента,

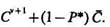
(9.24)

При 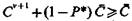рационально принять решение на v-m эксперименте, а при 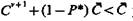рационально проводить (v+ 1)-эксперимент.

Перепишем неравенствов виде и положим, что a_j=a₀ при всех j==1, ..., r. Тогда выбранное значение вероятности ошибочного решения

(9.25)

Критерий идеального наблюдателя (критерий Зигерта—Котельникова). В случае, когда нет возможности определить а_и, решение о принадлежности объекта тому или другому классу может быть принято на основе критерия идеального наблюдателя, обеспечивающего минимум ошибочных решений.

Пусть все множество объектов подразделено на классы Ω₁ и Ω₂ и априорные вероятности появления объектов этих классов равны Р(Ω₁)и Р(Ω₂). соответственно. Кроме того, стоимости правильных решений с₁₁=с₂₂=0, а стоимости ошибочных решений c₁₂ = c₂₁.

Критическое (пороговое) значение отношения или коэффициента правдоподобия в этом случае равно отношению априорных вероятностей:

(9.26)

Пусть экспериментально установлено, что значение признака у распознаваемого объекта будет х=х⁰. Тогда коэффициент правдоподобия

(9.27)

В соответствии с критерием идеального наблюдателя объект относится к классу Ω₁ если l(х⁰)<l₀, и относится к классуΩ₂, если l(х⁰)>l₀

Если установлено значение х₀, при котором имеет место равенство P(Ω_l)f_l(x₀) = P(Ω₂)f₂(x₀), то в соответствии с рассматриваемым критерием объект относится к классу Ω₁, если измеренное значение признака этого объекта х⁰<х₀, и к классу Ω₂, если х⁰>x₀.

Критерий идеального наблюдателя совпадает с критерием максимума апостериорной вероятности, когда число классов m=2. В соответствии с критерием максимума апостериорной вероятности решение о принадлежности объекта классу Ω_r, r= 1, ..., m, принимается тогда, когда апостериорная вероятность отнесения объекта к этому классу больше, чем апостериорная вероятность отнесения его ко всем остальным классам, т. е. wÎΩ_r, если Р(Ω_r|х⁰)=mахР(Ω_r|х⁰), i=1, ..., m.

Апостериорные вероятности того, что объект относится к классам Ω₁ и Ω₂, соответственно равны.

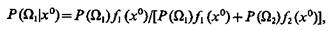
(9.28)

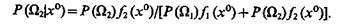
(9.29)

Объект относится к классу Ω₁ если

(9.30)

и к классу Ω₂, если

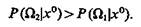
(9.31)

Граница соответствует равенству

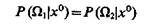
(9.32)

или с учетом (9.29) и (9.30) — равенству

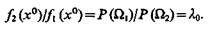
(9.33)

Таким образом, критерий максимума апостериорной вероятности, как и критерий идеального наблюдателя, предусматривает в качестве порога критическое значение коэффициента правдоподобия.

Критерий заданного превышения максимальной апостериорной вероятности над суммарной апостериорной вероятностью всех остальных гипотез. Пусть в результате проведения экспериментов установлены значения признаков {x₁ = x₁⁰, ..., x_N=x_N⁰) распознаваемого объекта и пусть, кроме того, 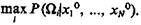В соответствии с рассматриваемым критерием решение о принадлежности распознаваемого объекта к классу Ω_r, r=l, ..., m, принимается в случае, если

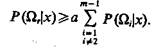
(9.34)

Применение подобного критерия оправдано в случаях, когда решение о принадлежности распознаваемого объекта Ω_r-му классу сопряжено со значительным риском.

Принятие решений при неполных данных. В ряде практически важных случаев не представляется возможным измерить всю совокупность признаков, используемых для описания объектов. Подобная ситуация имеет место из-за самых разнообразных причин. Например, у врача может не оказаться под рукой той или другой аппаратуры, необходимой для определения соответствующих симптомов заболевания; геолог в полевых условиях, как правило, лишен возможности произвести подробные исследования физических и химических свойств исследуемых материалов, и т. д. Уже говорилось, что в самом общем случае планирования работы систем распознавания решение на проведение очередной серии экспериментов или о прекращении экспериментов производится именно при неполных данных, т. е. когда известна лишь часть признаков, характеризующих распознаваемый объект. В подобных ситуациях решающее правило может быть основано на критерии максимума апостериорной информации. Рассмотрим основные методы решения задачи.

Метод 1. Он может быть использован, когда известна условная плотность вероятности значений любого, наперед заданного подмножества признаков, принадлежащего множеству признаков рабочего словаря.

Положим, что заданы алфавит классов Ω_i i= 1, ..., m, априорные вероятности Р(Ω_i) рабочий словарь признаков х = {х₁ ..., x_N}, условные плотности распределения f_i(x_j₁ ..., x_jk), где {j₁ ..., j_k}Î {l,...,N},k£N.

Пусть в результате проведения экспериментов установлены значения некоторых признаков (x_j₁=x⁰_j₁, ..., x_jk=x⁰_jk) распознаваемого объекта. Обозначим это событие b и определим значения апостериорной вероятности принадлежности объекта со классам:

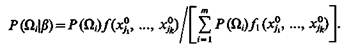
(9.35)

Решающее правило, основанное на критерии максимума апостериорной вероятности, состоит в следующем: wÎΩ_r, если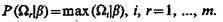

Метод 2. Он может быть применен, когда удается определить наиболее вероятные значения признаков, не определяемых экспериментально, и, как и в предыдущем методе, стоимости правильных решений c₁₁ = c₂₂ = 0, а стоимости ошибочных решений c₁₂ = c₂₁.

Обозначим b событие, состоящее в том, что в результате экспериментов установлены значения признаков x_l = x₁⁰, ..., x_N_-1= x⁰_N_-1объекта со и, кроме того, x_N-_k₊_l =x*_N-_k₊₁ ..., x_N=x*_N, где x*_N-_k₊₁ ..., x*_N — наиболее вероятные значения признаков объекта e, которые экспериментально не определены. Значения апостериорной вероятности принадлежности объекта w классам таковы:

(9.36)