Эффективность логических систем распознавания
При построении логических систем распознавания приходится сталкиваться с ситуацией, когда значения истинности элементов А1..., Аn, выражающих признаки объектов, принадлежащих классам Ωl, ..., Ωm и связанных с элементами А1 ..., Аn соотношениями Е(А1 ..., Аn; Ωl, ..., Ωm) = l, устанавливаются в процессе эксперимента или по данным наблюдений не достоверно, а с известной неопределенностью. Это случается либо когда элементы Ai , i=l, ..., n, обозначают высказывания «истинное значение xi, параметра Xi лежит в пределах интервала (ai, bi)», причем результат измерения Xi есть случайная величина, либо когда определение признаков элементов А1, ..., Аn производится в условиях естественных или искусственных помех, благодаря чему создаются предпосылки для ошибочных заключений.
К каждой проектируемой системе распознавания, как правило, предъявляются требования, касающиеся степени определенности ответов, выдаваемых системой в форме булевых функций j(Ωl, ..., Ωm), которые в общем случае удовлетворяют соотношению импликации  где f(A1 ..., Аn) — известная в результате эксперимента функция, А1 ..., Аn и Ωl, ..., Ωm — элементы, связанные зависимостями вида E(Ai Ωj)= 1.
где f(A1 ..., Аn) — известная в результате эксперимента функция, А1 ..., Аn и Ωl, ..., Ωm — элементы, связанные зависимостями вида E(Ai Ωj)= 1.
Из множества допускаемых данной системой решений j(Ωl, ..., Ωm) практически полезными могут быть лишь некоторые. Вид решения j(Ωl, ..., Ωm) помимо априорных соотношений существенно зависит от полноты сведений об объекте, которые представляются функцией f(A1, ..., Аn).
Предположим, что для практических целей важно различать N наблюдаемых во время эксперимента классов объектов, описываемых булевыми функциями  причем при
причем при 
Вид функций ji должен определяться требованиями, которые предъявляются к системе распознавания.
Пусть  есть множество всех простых импликант функции ji(Ωl, ..., Ωm), так что каждая функция fi из множества {fi} удовлетворяет соотношению
есть множество всех простых импликант функции ji(Ωl, ..., Ωm), так что каждая функция fi из множества {fi} удовлетворяет соотношению  Вследствие условия ji × jj=0 при i¹j функции f1 ..., fN должны удовлетворять соотношениям fi×fj®0 при i¹j или соотношениям fi×fj=0.
Вследствие условия ji × jj=0 при i¹j функции f1 ..., fN должны удовлетворять соотношениям fi×fj®0 при i¹j или соотношениям fi×fj=0.
Если при всех i= 1, ..., N функции  то, согласно сделанным предположениям, выбранный способ описания объектов позволяет различать между собой все N классов как с точки зрения их представления функциям
то, согласно сделанным предположениям, выбранный способ описания объектов позволяет различать между собой все N классов как с точки зрения их представления функциям  так и с точки зрения их представления функциями fi(A1, ..., Аn), т. е. через наблюдаемые или оцениваемые в опыте признаки А1 ..., Аn. При этих условиях ошибочные или неопределенные решения
так и с точки зрения их представления функциями fi(A1, ..., Аn), т. е. через наблюдаемые или оцениваемые в опыте признаки А1 ..., Аn. При этих условиях ошибочные или неопределенные решения  могут возникать только из-за того, что значения истинности элементов А1 ..., Аn устанавливаются во время опыта с ошибками или же вообще не устанавливаются.
могут возникать только из-за того, что значения истинности элементов А1 ..., Аn устанавливаются во время опыта с ошибками или же вообще не устанавливаются.
Обозначим ру вероятность получить решение ji(Ωl, ..., Ωm), т. е. j(Ωl, ..., Ωm)® ji(Ωl, ..., Ωm), i=1, ..., N, при условии, что распознаваемый объект является объектом j-го типа, т. е. функция f(A1, ..., Аn) в соотношении f(A1, ..., Аn)®ji(Ωl, ..., Ωm) задается как f=fj(A1, ..., Аn)
Чтобы количественно описать процесс искажения информации об объектах во время опыта, введем в рассмотрение следующие величины:
 — вероятность того, что в результате опыта будет установлено Ai=1, когда фактически Ai = 1;
— вероятность того, что в результате опыта будет установлено Ai=1, когда фактически Ai = 1;
 — вероятность того, что значение истинности элемента Ai не будет установлено (Ai = ´), когда в действительности Ai = 1;
— вероятность того, что значение истинности элемента Ai не будет установлено (Ai = ´), когда в действительности Ai = 1;
 — вероятность того, что ошибочно будет принято Ai=0, тогда как на самом деле Ai= 1, и аналогичные по смыслу вероятности
— вероятность того, что ошибочно будет принято Ai=0, тогда как на самом деле Ai= 1, и аналогичные по смыслу вероятности 
 при условии, что фактически значением истинности элемента Ai является Ai =0.
при условии, что фактически значением истинности элемента Ai является Ai =0.
Очевидно, что величины qi удовлетворяют условиям
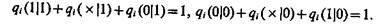
(10.2)
Установим зависимость величин рij от вероятностей qi(1|1),
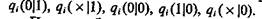
Пусть наблюдаемый в процессе эксперимента конкретный объект характеризуется каким-либо определенным набором признаков, выраженных через значения истинности элементов А1 ..., ..., Аn. Устанавливаемые в результате опыта значения истинности элементов Ai могут отличаться от тех значений, которые присущи данному объекту. Будем предполагать, что события, состоящие в установлении значений истинности элементов А1 ..., Аn, в результате эксперимента — независимые, так что вероятность одновременного наступления каких-либо событий равна произведению вероятностей этих событий.
При заданных фактических значениях истинности элементов А1 ..., Аn у наблюдаемого объекта все возможные исходы эксперимента, производимого над данным объектом, определяются вероятностями  Множество 3n несовместных исходов эксперимента вместе с отнесенными им вероятностями образует пространство элементарных событий рассматриваемого опыта.
Множество 3n несовместных исходов эксперимента вместе с отнесенными им вероятностями образует пространство элементарных событий рассматриваемого опыта.
Выберем из пространства элементарных событий точки, которые совпадают с множеством {fi(A1 ..., Аn)} всех импликант функции ji(Ωl, ..., Ωm). Сумма вероятностей, отнесенных к этим точкам пространства элементарных событий, равна вероятности P[ji|f(A1 ..., Аn)] получить решение вида ji(Ωl, ..., Ωm) при условии, что распознаваемый объект характеризуется определенным набором признаков, выраженных через фиксированные значения истинности элементов А1 ..., Аn как булева функция f(A1 ..., Аn)=1. Множество всех типов объектов, принадлежащих каждому классу описываемых функциями ji(Ωl, ..., Ωm), определяется суммой импликант 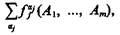 записанной в СДНФ.
записанной в СДНФ.
Если ввести в рассмотрение вероятности rajj появления объектов различных типов aj внутри каждого класса ji(Ωl, ..., Ωm),), то величины рij выразятся как 
Обозначим Сij, i, j=l, ..., N, выигрыш (штраф), выплачиваемый при отнесении объекта го класса к i-му классу, a CN+1j — выигрыш (штраф), выплачиваемый в случае, когда об объекте из j-го класса не удается получить определенного решения вида ji(Ωl, ..., Ωm). Тогда

(10.3)
будет средним выигрышем на одно решение при условии, что объект взят из j-го класса.
Пусть, наконец, Qj обозначает априорную вероятность появления объекта из j-го класса. Тогда
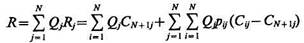
(10.4)
будет безусловным средним выигрышем на одно решение в данной системе распознавания.
Различные системы, предназначенные для распознавания одних и тех же объектов, но отличающиеся либо способами определения значений истинности признаков А1 ..., Аn и, следовательно, значениями вероятностей 
 либо самой совокупностью признаков Ai привлекаемых для описания объектов, можно сравнивать между собой по значению величины R. Величина R характеризует степень приспособленности системы для решения стоящих перед ней задач в тех практических условиях, которые определяются вероятностями rajj, Qj и стоимостями Сij, CN+lj, и потому может быть принята в качестве критерия эффективности системы распознавания.
либо самой совокупностью признаков Ai привлекаемых для описания объектов, можно сравнивать между собой по значению величины R. Величина R характеризует степень приспособленности системы для решения стоящих перед ней задач в тех практических условиях, которые определяются вероятностями rajj, Qj и стоимостями Сij, CN+lj, и потому может быть принята в качестве критерия эффективности системы распознавания.
Определив R и его зависимость от основных факторов, влияющих на правильность распознавания объектов, можно поставить задачу построения оптимальной системы распознавания, которой отвечает экстремальное значение критерия эффективности R, и при этом не нарушаются условия, налагаемые на основные факторы в форме нестрогих неравенств и ограничивающие множество допустимых способов реализации данной системы. В качестве основных факторов, влияющих на критерий эффективности R, могут быть выбраны некоторые технические характеристики аппаратуры, используемой для выявления признаков А1 ..., Аn объектов, или же различные способы ее применения.
Пример. Требуется оценить эффективность системы распознавания объектов, описываемых признаками A1¸A4, связанными с классами Ω1, Ω2, Ω3 зависимостью :

(10.5)
Пусть заданы функции

(10.6)
Допустим, что элемент А1 обозначает высказывание «истинное значение xi измеряемого параметра Xi принадлежит интервалу (ai,b i)»:
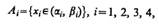
(10.7)
a `Ai есть утверждение

причем отрезки (ai,b i) и (li,gi) не имеют общих точек (рис. 10.2).
Измеряемые параметры Xi представляются в виде

где xi равномерно распределена либо в (ai,b i), либо в (lji,di), a xi¢ имеет нормальное распределение с нулевым математическим ожиданием с среднеквадратичным отклонением si, т. е. плотность случайной величины xi¢

(10.8)

Рис. 10.2
Обозначим a¢i, b¢i граничные точки некоторого интервала, охватывающего (ai,b i), a (g¢i,d¢i) — граничные точки другого интервала, охватывающего gi, di (рис. 10.2), и примем следующее решающее правило: будем считать, что хiÎ(ai,bi), если измеренное значение XÎ(a¢i,b¢i), и xiÎ(gi,di), если измеренное значение XiÎ(g¢i,d¢i). В соответствии с этим из (10.7) и (10.8) найдем

(10.9)
где 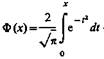 — функция Лапласа.
— функция Лапласа.
Точно так же

(10.10)
где  — внешние части отрезков
— внешние части отрезков 
И аналогично,

(10.11)
При заданных ai,b i, gi,li можно варьировать значения a¢i,b¢i, g¢i,d¢i так, чтобы вероятности qi(1|1), ..., qi(´|0) соответствовали экстремальному значению показателя эффективности системы распознавания.
Найдем первые импликанты функций j1, j2, j3, j4 заданных (10.6). Соотношение (10.5) трансформируется в следующую таблицу сокращенного базиса b´[A1,A2,A3,A4;Ω1,Ω2,Ω3]:

(10.12)
Совершив переход от базиса b´[A1,A2,A3,A4;Ω1,Ω2,Ω3] к базису bс[A1,A2,A3,A4;Ω1,Ω2,Ω3] получим

(10.13)
Последние три строки базиса (10.13) — изображающие числа функции Ω1(A1,A2,A3,A4), Ω2(А1, А2, А3, А4), Ω3(A1,A2,A3,A4) относительно полного стандартного базиса b[A1,A2,A3,A4]юПереходя от изображающих чисел к функциям, найдем

(10.14)
Так как  то
то

(10.15)
и, кроме того,

(10.16)
Для определения первых импликант функций jj можно было бы воспользоваться базисом (10.12) без перехода (10.13), что существенно при большом числе элементов Ai. Например, покажем, как найти первые импликанты функции j1=`Ω1,`Ω2,`Ω3.
Перейдем к отрицанию j1 т.е 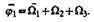 С колонкой
С колонкой 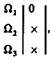 отвечающей `Ω1, сравнимы пять последних правых колонок базиса (10.12), поэтому
отвечающей `Ω1, сравнимы пять последних правых колонок базиса (10.12), поэтому  или после преобразования
или после преобразования 
Аналогично с помощью оазиса (10.12) находим

откуда  После обращения
После обращения

(10.17)
Левая часть (10.17) совпадает с правой частью первого соотношения (10.14). Представим суммы (10.15) первых импликант функций в СДНФ:

(10.18)
Каждое слагаемое в (10.18) — конкретный тип faj j-то объекта из соответствующего класса jj,j,= 1, 2, 3, 4, а значения индекса о,-— номера типов объектов в пределах каждого класса.
Рассмотрим объект класса j1 первого типа:
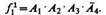
(10.19)
Найдем вероятность P(j1|f11), с которой объект (10.19) будет отнесен при распознавании к классу j1. Для этого в соответствии с (9.18) выпишем полный набор импликант функции 

(10.20)
Вероятность P(j1|f11)равна вероятности воспринять на опыте признаки объектаf11=А1×А2×A3×`A4 как какую-либо импликанту из набора (10.20):

Объединим в этом выражении первый, второй и третий, пятый и девятый, шестой, десятый и одиннадцатый члены, а также три оставшихся и воспользуемся равенствами 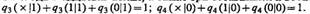 . В результате получим
. В результате получим

Так как  то в соответствии с формулой для вероятности суммы нескольких событий найдем
то в соответствии с формулой для вероятности суммы нескольких событий найдем

(10.21)
Учитывая (10.15) и (10.16), по аналогии с (10.21) получим

(10.22)
Точно так же могут быть определены и все оставшиеся 15´4=60 величин P(j1|fajj), где fajj обозначает aj-й объект в классе jj.
Предположим, что как появление объектов из различных классов, так и распределение отдельных объектов в пределах каждого класса равновероятны. Тогда вероятности рij, определенные выражением  запишутся так:
запишутся так:

Значения средних условных выигрышей на одно решение будут равны:
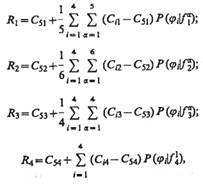
где Cij,j= 1, 2, 3, 4 — выигрыш, когда объект из j-го класса принимается за объект из i-го класса; С5j — размер платежа, когда об объекте из j-го класса не принимается никакого решения.
Безусловный средний выигрыш на одно решение

Как уже отмечалось, величина R существенно зависит от значений a¢i,b¢i, g¢i,d¢i, i=1, 2, 3, 4, входящих в вероятности qi(1|1), ..., qi(х|0), определенные (10.9) — (10.11). Параметры a¢i,b¢i, g¢i,d¢i могут быть связаны рядом условий вида

(10.23)
которые имеют смысл ограничений, накладываемых на стоимость, надежность, энергопотребление, массу, габариты и другие характеристики аппаратуры, используемой для измерения в опытах значений величин Xi. Тогда задача построения оптимальной системы распознавания приводится к отысканию, например,  при ограничениях (10.23).
при ограничениях (10.23).
Когда число признаков А1 ..., Аn объектов велико, вычисление значений критерия эффективности системы распознавания R представляет собой, как правило, трудную задачу. Основные трудности — в множественном переборе объектов различных классов fajj при подсчете вероятностей P(ji|fajj) и применении формулы для вероятности суммы большого числа совместных событий. Для преодоления этих трудностей также можно использовать метод Монте — Карло (метод статистических испытаний). Общая идея этого метода — в моделировании и многократном повторении условий опыта по определению признаков A1, ..., Аn известных типов объектов и применению решающего правила для установления класса испытываемого объекта. Подсчитав число Naji решений, приводящих к заключению ji(Ω1 ,... Ωm) при фиксированном типе объекта fajj, можно дать оценку значения вероятности P(ji|fajj), если разделить Najj на общее число Naj испытаний, проведенных с объектом типа fajj, т. е. 

Число испытаний N, необходимое для того, чтобы вероятность отклонения оценки величины  от своего истинного значения меньше чем на 2d превышала 1-e, определяется по формуле [34]
от своего истинного значения меньше чем на 2d превышала 1-e, определяется по формуле [34]

(10.24)
Исходными данными для метода Монте — Карло в задаче служат:
1. Таблица сокращенного базиса bс[А1 ..., Аn; Ω1 ..., Ωm], представляющая собой различные типы объектов. Каждый столбец сокращенного базиса с точки зрения системы признаков А1 ..., Аn и классов Ω1 ..., Ωm можно рассматривать как определенный тип объекта fajj(А1 ..., Аn), входящий в рассматриваемое множество.
2.Значения вероятностей 
 характеризующие условия опыта, проводимого над объектами.
характеризующие условия опыта, проводимого над объектами.
3. Запрограммированный на ЭВМ алгоритм нахождения решения j(Ω1 ..., Ωm) системы булевых уравнений:

(10.25)
где Е(Аi; Ωj) — функция, представляющая собой наложенные на элементы Ai, и Ωj, связи; f(A1, ..., Аn) — функция, определяемая в результате опыта над классифицируемым объектом.
Построенная по этим исходным данным стохастическая модель распознавания объектов зависит от конкретных физических условий, при которых проводится опыт, а также от характеристик аппаратуры, предназначенной для определения признаков объектов через вероятности qi(1|1), ..., qi(´|0).
Опишем алгоритм работы рассматриваемой модели. Предположим, что указанные исходные данные занесены в память ЭВМ. Обозначим xm m-ю реализацию случайной велияины x, равномерно распределенной в интервале [0, 1]. Величина вырабатывается соответствующим датчиком случайных чисел каждый раз независимо.
Предположим, что произведено разбиение отрезка (0, 1) и раз на три части, пропорциональные  и еще n раз на три части, пропорциональные
и еще n раз на три части, пропорциональные  , i=l, 2, ..., n.
, i=l, 2, ..., n.
Испытания проводятся последовательно для каждого типа объекта fajj(А1 ..., Аn). Пусть объекту типа fajj(А1 ..., Аn)соответствует некоторая колонка сокращенного базиса bc[А1 ..., Аn; Ω1 ..., Ωm]. Перенесем эту колонку в v-ю рабочую ячейку памяти ЭВМ. В этой ячейке значения истинности признаков А1 ..., Аn, равные 0 или 1, случайным образом подвергаются изменению в соответствии со значениями вероятностей и
и  Для колонки с номером v процедура изменения значений истинности признаков Аi производится в такой последовательности. С помощью операции сравнения устанавливают содержимое i-го разряда v-й ячейки. Если Ai=l, то переходят к проверке условий
Для колонки с номером v процедура изменения значений истинности признаков Аi производится в такой последовательности. С помощью операции сравнения устанавливают содержимое i-го разряда v-й ячейки. Если Ai=l, то переходят к проверке условий

(10.26)
если Ai=0, то проверяют условия

(10.27)
где xm — реализация случайной величины x, равномерно распределенной в [0, 1].
Если Аi= 1 и выполняется первое условие (10.26), содержимое i-го разряда v-й ячейки не изменяется, если выполняется второе условие (10.26), то Аi = 1 заменяется на Аi =0, если имеет место последнее неравенство (10.26), то Ai= 1 заменяется на Аi = ´.
Если Аi =0 и удовлетворяется первое из условий (10.27), то Ai=0 сохраняется неизменным; если выполняется второе условие (10.27), то Ai=0 заменяется на Ai= 1, если выполняется последнее условие (10.27), то содержимое i-го разряда v-й ячейки заменяется на Ai= ´.
Переходят к следующему (i+ 1)-му разряду v-й ячейки и для очередной (m+ 1)-й реализации xm+1 случайной величины x проверяются условия (10.26) или (10.27).
Измененная в соответствии с данными правилами v-я ячейка поступает на вход алгоритма решения задачи (10.25). После получения решения j(Ω1 ..., Ωm) устанавливается, какой из случаев

(10.28)
реализуется при заданном типе распознаваемого объекта fajj(А1 ..., Аn). В результате многократного повторения описанного процесса по дочитываются количества Naji выпадений каждого из Najслучаев (10.28) и определяются оценки величин P(ji|fajj).