Системы распознавания без обучения
Построение систем распознавания без обучения возможно при наличии полной первоначальной априорной информации, которая представляет собой совокупность: 1) сведений о том, какова естественная или социальная природа объектов или явлений, для распознавания которых предназначается создаваемая система, какие решения могут и будут приниматься на основе результатов распознавания. Подобные сведения — исходные для определения принципа классификации и проведения собственно классификации, т. е. подразделения всего множества объектов или явлений на классы; 2) данных, обеспечивающих построение априорного словаря признаков системы распознавания, и сведений относительно ограничений, накладываемых на создание измерительной аппаратуры системы; 3) зависимостей между классами объектов Ωi, i=l, ..., m, и признаками априорного словаря ха = {х1 ..., xN}, которыми они характеризуются, или сведений, достаточных для непосредственного составления подобных зависимостей.
Описание классов на языке признаков после составления алгоритмов распознавания, базирующихся на соответствующей мере близости, позволяет решить задачу построения рабочего словаря признаков системы распознавания и затем вновь вернуться к задаче описания классов, но уже на языке признаков рабочего словаря xр = {хj1, ..., xjn}, где j1 ...,jnÎ1, ..., N.
Для обсуждения задачи накопления и анализа априорной информации, носящей логический характер, и описания классов на языке логических признаков требуются специальные знания в области алгебры логики. Именно поэтому данная задача рассматривается непосредственно вслед за изложением основ теории алгебры логики.
Построение функций fi(x1 ..., xN). Когда признаки — вероятностные, то описаниями классов являются условные плотности распределения вероятностей значений признаков х1 ..., xN для каждого класса Ω1 ..., Ωm, т. е. функции fi(х1 ..., xN), а также априорные вероятности P(Ωi), i'=1,..., m, появления объектов соответствующих классов.
При построении функций плотности fi(x1 ..., xN) следует различать две ситуации. В первой ситуации априори известен аналитический вид функции плотности, содержащей некоторое количество параметров, которое и надлежит оценить {параметрическая оценка). Во второй ситуации вид функции неизвестен. В этой более сложной ситуации необходимо произвести оценку и вида функции плотности, и их параметров (непараметрическая оценка).
Параметрическая оценка. Параметрическая оценка функции плотности возможна лишь в достаточно простых ситуациях. Она может быть выполнена при использовании следующих методов.
Метод максимума правдоподобия Фишера. Это наиболее общий метод нахождения оценок параметров функции плотности. Идею метода можно представить следующим образом [9]. Пусть m-мерная случайная величина X задана функцией плотности вида f(x, q), где q — неизвестный параметр или вектор параметров, и выборкой независимых реализаций х1 ..., хN объемом N, которую можно представить в виде выборки объемом 1, принадлежащей системе N независимых одинаковых m-мерных случайных величин X1, ..., XN. Общая мерность системы mN. Реализацию, составляющую эту выборку, можно представить в виде вектора длиной N, каждый из компонентов которого есть m-мерная величина 
Значение совместной функции плотности такой системы случайных величин в точке  и называется функцией правдоподобия (функцией параметра q). Значение параметра q, при котором она достигает максимума, называется оценкой максимального правдоподобия параметра q.
и называется функцией правдоподобия (функцией параметра q). Значение параметра q, при котором она достигает максимума, называется оценкой максимального правдоподобия параметра q.
Оценки максимального правдоподобия обычно определяю, максимизируя  и пользуясь тем, что In x— строго возрастающая функция. Искомое значение q находится из уравнения
и пользуясь тем, что In x— строго возрастающая функция. Искомое значение q находится из уравнения
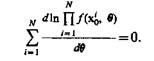
(3.1)
Если q — вектор длиной r, то уравнение представляет собой систему r уравнений относительно компонентов вектора q.
Метод Байеса. Здесь, как и в предыдущем методе, функция плотности задается также параметрически, но параметр q считается величиной случайной с известной априорной плотностью распределения f(q). Таким образом, задается не просто множество допустимых функций плотности, из которых следует выбрать одну-единственную, а задаются и их априорные вероятностные веса. Апостериорные вероятностные веса q рассчитываются по выборке х1 ..., xN, полученной в соответствии с плотностью f(х).
Оценка функции плотности при этом определяется как непрерывная смесь плотностей с апостериорными вероятностными весами

(3.2)
где Аq — область возможных значений q.
Апостериорная функция плотности q определяется по правилу Байеса:

(3.3)
Если при параметрической оценке вид функции плотности задан предположительно (гипотетически), то оценка функции плотности не заканчивается выбором ее параметров. Необходимо убедиться, не противоречит ли гипотеза о виде функции плотности эмпирической информации. Наиболее универсальным методом проверки такой гипотезы является критерий c2 Пирсона [9]. Он не зависит ни от истинной функции плотности, ни от ее мерности.
В качестве меры отклонения эмпирической функции плотности (гистограммы, в общем случае многомерной) от гипотетической рассматривается величина
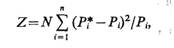
(3.4)
где N — количество реализации в выборке; n — количество интервалов разбиения при построении гистограммы (в многомерном случае — многомерных кубов); Рi* — частота попадания реализации в i-й интервал в N реализациях; Рi — вероятность попадания в i-й интервал, вычисленная по гипотетической функции плотности.
Д. Нейман и К. Пирсон доказали, что если для вычисления вероятностей Р1 ..., Рn применяется асимптотически эффективная и асимптотически нормальная оценка неизвестного S-мерного параметра гипотетической функции плотности (например, полученная методом максимального правдоподобия), то при N®¥ Z имеет распределение c2 с n —S—1 степенями свободы. Тогда при предположении, что N достаточно велико, вероятность того, что Z превзойдет некоторую величину cр2 определится равенством
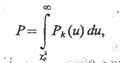
(3.5)
где k=n — S— 1.
Зададимся достаточно малой величиной Р, такой, что событие с этой вероятностью будем считать практически невозможным. Из равенства (3.5) определим c2- Если Z³c2p, то гипотетическую функцию плотности считают противоречащей экспериментальным данным, так как при этом практически невозможно получить Z³c2p.
Непараметрическая оценка. Параметрическое оценивание плотности допустимо лишь в достаточно простых ситуациях. При большом числе признаков, неизвестной зависимости между ними, неясности физического смысла класса и т. п. предсказать достаточно удовлетворительно аналитический вид функции плотности обычно невозможно. Оценку функции плотности в таких случаях целесообразно получать непараметрическими методами.
При этом всегда предполагается, что искомая функция плотности непрерывна или, по крайней мере, имеет незначительное по сравнению с объемом выборки число разрывов.
Многие непараметрические методы опираются на возможность оценивания по выборке вероятности появления реализации в заданной области значений рассматриваемой случайной величины [10].
Вероятность попадания одной реализации в область А

(3.6)
Вероятность попадания к реализаций из выборки объемом N в область А
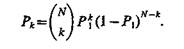
(3.7)
Если рассматривать k как случайную величину при фиксированных А и N, то математическое ожидание k равно P1N. Биноминальное распределение вероятности для к (3.7) имеет при достаточно больших N выраженный максимум около среднего значения. Поэтому можно приближенно полагать, что число реализаций в данной выборке, попавших в А, равно их математическому ожиданию, т. е.

(3.8)
Отсюда P1»k/N. Если обозначить VA объем области А, то можно считать выражение
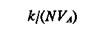
(3.9)
оценкой среднего значения плотности в А.
Гистограммный метод. Это наиболее простой метод непараметрической оценки, базирующийся на оценке средней плотности распределения в области [9, 11].
Построение гистограммы предполагает разбиение всей области возможных значений X на конечное число интервалов (в многомерном случае — «прямоугольных») и подсчет количества реализаций, попадающих в каждый из них. Оценка плотности распределения признаков в области Ai при этом

(3.10)
где ki — количество реализаций, попавших в область Ai, Vi — объем области Аi.
Для m-мерной случайной величины

где hfi — размер области Ai по j-му признаку.
Обычно применяют два способа построения гистограммы — с одинаковыми по объему областями разбиения или с различными (так, чтобы в каждую попало примерно одно и то же число реализаций).
Основное преимущество гистограммы — простота построения, недостатки — неопределенность при выборе способа разбиения пространства признаков и, следовательно, существенный элемент субъективизма в оценке и неудовлетворительность оценки вблизи границ областей разбиения, где оценка претерпевает разрывы. Отсюда возникает необходимость в процедуре сглаживания. В многомерном случае эта задача чрезвычайно сложна. Оценку функции плотности в виде гистограммы можно полагать удовлетворительной только при весьма больших выборках.
Методы локального оценивания. На использовании формулы (3.9) базируются и методы локального оценивания (получения оценки плотности в заданной точке). Для оценки плотности в точке х учитывают реализации, которые попадают в малую окрестность точки х0. Обычно окрестность берется в виде гипершара или гиперкуба.
Объем гипершара с эвклидовым радиусом R равен bmRm, где

С увеличением N объем окрестности х0 уменьшается. Если плотность в точке х0 непрерывна и последовательность окрестностей по мере увеличения N стягивается к точке х0 достаточно медленно, так что среднее число реализаций, попадающих в окрестность, неограниченно возрастает при N®¥, то оценка плотности в точке х0 оказывается состоятельной.
Существуют два общих метода получения последовательностей окрестностей х0, удовлетворяющих этим условиям.
Первый (метод «парзеновского окна») заключается в сжатии некоторой первоначально заданной окрестности объемом V1 как некоторой функции от N, такой, что
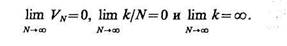
(3.11)
Этим условиям удовлетворяют, например, зависимости VN=V1ÖN,VN=V1/logN и т. п. Одна из проблем, с которой сталкиваются при использовании метода «парзеновского окна», заключается в выборе конкретного вида зависимости VN от N, поскольку существует много функций, удовлетворяющих условиям (3.11). Недостатком данного метода является также высокая чувствительность оценки к выбору первоначального объема V1 и то, что объем окрестности, удовлетворительный для одного x0 (отвечающий условиям разумного компромисса между достаточной статистической устойчивостью оценки и не слишком сильным усреднением), может оказаться совершенно неудовлетворительным для другого х0.
Второй метод (<<kN ближайших соседей») отличается от первого тем, что объем окрестности x0 задается функцией не только N, но и фиксированного числа kN реализаций, ближайших к x0. В качестве расстояния между х0 и реализациями обычно используется эвклидова мера. В данном случае окрестность x0 увеличивается до тех пор, пока она не будет включать kN реализаций (где kN — функция от N). В качестве функций kN от N, удовлетворяющих условиям (3.11), можно, например, взять kN=-ÖN, kN= logN и т. п.
Метод «kN ближайших соседей» [10, 11] сохраняет тот же недостаток, что и метод «парзеновского окна»,— неопределенность в выборе зависимости kN от N.
Таким образом, методы локального оценивания обладают двумя существенными недостатками: 1) необходимостью хранить в памяти всю обучающую выборку, что неудобно при больших N; 2) отсутствие критериев однозначного выбора зависимостей VN от N или kN от N.
Оба метода локального оценивания плотности обеспечивают сходимость при N®¥, но при конечном объеме выборки трудно что-либо сказать об их качестве. Однако предполагается, что эффективность подходов, основанных на прямом фиксировании границ областей, ниже эффективности процедур, использующих локальное оценивание.
« Еще одна группа методов непараметрического оценивания основывается на том убеждении, что для непрерывной функции плотности в некоторой малой окрестности каждой из реализаций выборки значение плотности существенно отлично от нуля. Чем меньше окрестность, тем больше уверенность в справедливости этого предположения.
Исходя из этого, структура оценки представляется в виде суммы N весовых функций (ядер), «навешиваемых» на каждую реализацию. Такого рода оценка называется обобщенной гистограммой или оценкой парзеновского типа. В самом общем виде она представляется выражением
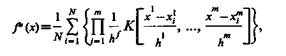
(3.12)
где К — функция, называемая ядром; h — коэффициент «размытости», являющийся функцией от N; m — мерность пространства признаков.
Для круговых ядер (К есть функция от R) оценка парзеновского типа определяется выражением
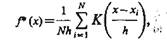
(3.13)
где x—xi — расстояние от х до xi взятое в соответствии с выбранной мерой.
К оценке парзеновского типа приводит и классический подход к конструированию оценки плотности путем дифференцирования эмпирического закона распределения вероятности [9, 10, 11].
При использовании в одномерном случае единичной ступенчатой функции интегральный эмпирический закон можно представить в виде
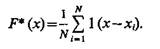
(3.14)
Дифференцируя это выражение и учитывая, что производная единичной ступенчатой функции представляет собой d-функцию, получим оценку плотности в виде
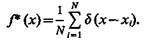
(3.15)
В случае непрерывной величины X эта оценка не может быть близкой к f(x) ни при каких значениях х и N. Эта оценка несостоятельна. Сделать ее состоятельной можно, если заменить d-функцию некоторой непрерывной плотностью. Если обозначить такую плотность (l/h)K[(x—xi)/h], то приходим к выражению (3.12) для одномерного случая.
Обобщенная гистограмма является асимптотически несмещенной и состоятельной, если 
К недостаткам обобщенной гистограммы можно отнести, во-первых, то, что число слагаемых равно числу реализаций (неудобно при большом количестве N), и, во-вторых, неоднозначность оценки в зависимости от выбора h = j(N) и конкретного вида ядра. Для оптимизации оценки, получаемой данным методом, необходима дополнительная эвристическая информация.
Одним из наиболее общих принципов непараметрического оценивания является приближенное представление искомой плотности в виде линейной комбинации некоторых базисных функций [8, 9, 12]. При этом возможны два основных варианта:
Вариант 1. Комбинация содержит конечное число функций, и задача сводится к оцениванию параметров линейной комбинации.
Вариант 2. Все функции и коэффициенты полностью известны, и необходимо выбрать такое подмножество слагаемых из этого множества, чтобы аппроксимация получилась достаточно точной.
При варианте 1

(3.16)
Если параметры функций q1 ..., qn заданы, то необходимо оценить неизвестные коэффициенты с1 ..., сn, что можно, в частности, осуществить методом максимума правдоподобия. В случае, когда q1 ..., qn неизвестны, приближенное представление плотности линейной комбинацией (3.16) сводится к совместному определению параметров функций и коэффициентов с1 ..., сn. При этом для достижения той же точности приближения можно взять меньше слагаемых в (3.16), но придется иметь дело с системой нелинейных уравнений. Если функции j1 ..., jn полагать функциями плотности, т. е. линейную комбинацию представить в виде смеси, то удается избежать возможных отрицательных значений оценки при вычислении по (3.16).
В варианте 2 наиболее типичным является аппроксимация неизвестной плотности линейной комбинацией ортогональных базисных функций:

(3.17)
Если базисные функции удовлетворяют условию
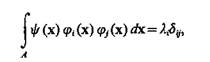
(3.18)
где

то говорят, что функции ji(х) ортогональные в области А с весом y (х). При этом коэффициенты разложения определяются следующим образом:
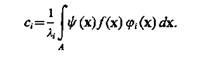
(3.19)
Если в разложении (3.17) ограничиться первыми л членами, то среднеквадратичная ошибка будет 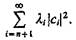 Если же удается найти систему базисных функций таких, что li |сi|2 быстро убывает с ростом i, то система дает экономное представление плотности. В общем многомерном случае процедура нахождения системы базисных функций неизвестна. Удобство представления неизвестной функции плотности линейной комбинацией функций состоит в том, что число функций можно брать значительно меньше объема выборки.
Если же удается найти систему базисных функций таких, что li |сi|2 быстро убывает с ростом i, то система дает экономное представление плотности. В общем многомерном случае процедура нахождения системы базисных функций неизвестна. Удобство представления неизвестной функции плотности линейной комбинацией функций состоит в том, что число функций можно брать значительно меньше объема выборки.
В случаях, когда имеется какая-либо априорная информация о функции плотности, рекомендуется с самого начала приписать оцениваемой плотности вероятности подходящий аналитический вид.
Построение функций Р(Ωi). Если априорная вероятность не зависит от времени, значения Р(Ωi) могут быть определены на основании частот событий:
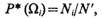
(3.20)
где N' — общее количество доступных изучению объектов во всех классах; Ni — количество объектов в i-м классе.
В некоторых системах распознавания, в частности в системах медицинской диагностики, Р(Ωi)может зависеть от времени. Это связано, например, с распространением эпидемии какого-либо заболевания, составляющего или входящего в определенный класс системы. Здесь следует изучить поведение функции Р(Ωi) во времени до текущего момента, а затем на основе тщательного изучения явления произвести их экстраполяцию на определенный промежуток времени.
Эвристический подход к описанию классов. Когда непосредственное изучение априорной информации невозможно, приходится прибегать к эвристическому конструированию законов распределений fi(xj), i=l, ..., m;j=1, ..., N, значений признаков по классам и функций Р(Ωi).
Задача определения функций fi(xj) может быть решена следующим образом. Положим, что группа квалифицированных специалистов, веса мнений которых Вk, k = 1, ..., n, согласилась дать экспертные оценки возможных значений признаков xj объектов всех классов. Пусть применительно к классу Ωi относительно признака xj эксперт Аk указал, что его значение составляет величину Сk(xj|Ωi)- При этом, во-первых, некоторые из значений признака xj объектов класса Ωi указанные разными экспертами, могут совпадать [например, Сg(xj|Ωi) = Сq(xj|Ωi), l£g, q£n]; во-вторых, отдельные эксперты могут указать на несколько возможных значений признака xj в Ωi-м классе [например, вероятны следующие значения признака: Сg(xj|Ωi), С²g(xj|Ωi) и т.д.]; в-третьих, кто-либо из экспертов может отказаться от указания о возможном значении некоторых признаков в ряде классов. Для наглядности суждения экспертов целесообразно свести в следующую таблицу:

Положим, что при определении значения признака xj применительно к объектам класса Ωi, эксперты подразделились на группы 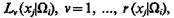 при этом число экспертов в группе
при этом число экспертов в группе  равно
равно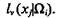 Пусть группа экспертов
Пусть группа экспертов указала, что значение признака xj в классе Ωi, составляет
указала, что значение признака xj в классе Ωi, составляет Усредненный вес мнений экспертов группы
Усредненный вес мнений экспертов группы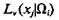
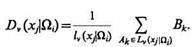
(3.21)
Будем полагать следующее: статистическая вероятность того, что значение признака xj у объектов, принадлежащих классу Ωi равно величине Cv(xj|Ωi), указанной группой экспертов Lv(xj|Ωi), пропорциональна усредненному весу мнений этой группы:
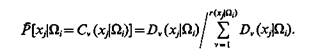
(3.22)
Это соотношение позволяет сформировать статистические ряды: 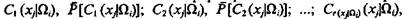
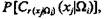 а на их основе путем сглаживания определить оценки искомых функций распределения вероятностей fi(хj).
а на их основе путем сглаживания определить оценки искомых функций распределения вероятностей fi(хj).
Метод определения функций P(Q,) аналогичен приведенному. Таким образом, эвристический подход к формированию априорных сведений основывается на обработке результатов опроса группы экспертов с учетом их авторитета. При этом предполагается, что научно-технический уровень экспертов достаточно высок, а их решения носят объективный характер.