Глава 1. Основы теории множеств

Авторское предисловие

 

Дорогой читатель, перед Вами книжка, которую мы довольно долго писали. Объясняется это прежде всего тем, что материал изложенный в ней сначала тщательно изучался в Учебно-методическом объединении по образованию в области информационной безопасности (Институт криптографии, связи и информатики Академии ФСБ в г. Москве), а затем в Министерстве образования РФ. Наконец книга у Вас в руках и мы надеемся, что она не окажется слишком сложной для Вас. Знания, которые Вы получите из этой книжки Вам пригодятся в дальнейшем, в частности, для усвоения криптографических методов защиты информации, прикладных алгоритмов, программных курсов и некоторых других важных дисциплин.

Данное пособие предназначено для студентов технических специальностей, у которых на курс математической логики отводится довольно мало часов. Поэтому, для того чтобы рассмотреть достаточно много вопросов нам пришлось пойти на сравнительно упрошенное изложение. При изложении материала мы считали, что вводимые понятия важнее теорем, а формулировки теорем важнее их доказательств.

Для начинающих изучение математической логики и теории алгоритмов мы предлагаем наиболее легкие и естественные доказательства. Очень важным, на наш взгляд, является то обстоятельство, что им вовсе не требуется специальных знаний для изучения этого курса, кроме "крепких" школьных знаний.

В пособии предлагается ряд распространенных логических парадоксов, на примере которых мы показываем трудности, возникающие в логике. Порой за простотой понятий и доказательств лежат глубинные, основополагающие принципы логического мышления. Излишне напоминать, что как любая наука математическая логика и теория алгоритмов требуют определенного уровня абстракции и некоторой математической культуры.

Очевидно, что в изложенном материале отсутствуют ряд разделов математической логики и теории алгоритмов. Сделано это нами сознательно в угоду желанию дать точные понятия наиболее важных тем. Авторы пособия не претендуют на глубокие исследования в области математической логики и теории алгоритмов. Наша цель куда более как скромна - дать базовые понятия и принципы, и побудить у обучаемых желание всерьёз заняться этой увлекательной наукой, поскольку изучение математической логики должно хотя бы немного стимулировать процессы мышления.

В учебное пособие включены разнообразные логические задачи, упражнения, которые позволяют закрепить теоретический материал.

Материал изложенный в пособии полностью соответствует государственному образовательному стандарту для специальностей "Комплексное обеспечение информационной безопасности автоматизированных систем", "Организация и технология защиты информации", а так же может быть использован для студентов других специальностей.

Пособие расcчитано на широкий круг читателей и рекомендовано Министерством образования РФ и Учебно-методическим объединением по образованию в области информационной безопасности для студентов обучающихся по специальностям в области информационной безопасности.

Данное учебное пособие можно использовать и как учебно-методические указания, поскольку практически в каждом параграфе пособия имеются примеры и упражнения с подробными указаниями и решениями.

Замечания и предложения направлять по адресу:

634050, Томск, пр-т Ленина, 40

ТУСУР кафедра КИБЭВС

тел. (83822) 413426

е-mail: office@keva.tusur.ru

 

 

В.М. Зюзьков,

А.А. Шелупанов
Чтобы что-то узнать, нужно уже что-то знать.

Станислав Лем

Всякое начало трудно, - эта истина справедлива для каждой науки.

К. Маркс

 

 

Глава 1. Основы теории множеств

 

Кто неправильно застегнул первую пуговицу, уже не застегнётся как следует.

Иоганн Вольфганг Гёте

Начальные понятия теории множеств

Понятие множества является основным, неопределяемым понятием, поэтому мы можем его только пояснить, например, с помощью следующего… Определение: Под множеством S будем понимать любое собрание определенных и… В этом интуитивном определении, принадлежащем немецкому математику Георгу Кантору (1845-1918), существенным является…

Интуитивный принцип объемности

Записывают A=B, если A и B равны, и A¹B - в противном случае. Пример 1.1. Проиллюстрируем принцип объемности. Множество A всех положительных… Множество, элементами которого являются объекты a1, a2,…, an и только они, обозначают { a1, a2,…, an }. При этом…

Операции над множествами. Диаграммы Венна

 

Рассмотрим методы получения новых множеств из уже существующих.

Определение. Объединением множеств A и B называется множество AЗB, все элементы которого являются элементами множества A или B:

AЗB = {x | xОA или xОB}.

Определение. Пересечением множеств A и B называется множество AИB, элементы которого являются элементами обоих множеств A и B:

AИB = { x | xОA и xОB}.

Очевидно, что выполняются включения AИB Н A Н AЗB и AИB Н B Н AЗB.

Определение. Относительным дополнением множества A до множества X называется множество XA всех тех элементов множества X, которые не принадлежат множеству A:

XA = {x | xОX и xПA}.

Определение. Симметрической разностью множеств A и B называется множество A+B = (AB)З(BA).

Определение. Если все рассматриваемые в ходе данного рассуждения множества являются подмножествами некоторого множества U, то это множество U называется универсальным для данного рассуждения (контекста).

Определение. Абсолютным дополнением множества A называется множество A всех тех элементов x, которые не принадлежат множеству A:

A = UX.

Заметим, что XA = XИA.

Для наглядного представления отношений между подмножествами какого-либо универсального множества используются диаграммы Венна. В этом случае множества обозначают областями на плоскости и внутри этих областей условно располагают элементы множества. Часто все множества на диаграмме размещают внутри квадрата, который представляет собой универсальное множество U. Если элемент принадлежит более чем одному множеству, то на диаграмме, области, отвечающие таким множествам, должны перекрываться, чтобы общий элемент мог одновременно находиться в соответствующих областях (рис.1).

 

 

A AÈB AÇB

 

 

 

AB BA A+B

 

Рис. 1. Диаграммы Венна

 

Теорема 1.1. Для любых подмножеств A, B и C универсального множества U выполняются следующие тождества (основные тождества алгебры множеств):

 

1. AЗB = BЗA (коммутативность З)	1'. AИB = BИA (коммутативность И)
2. AЗ(BЗC) = (AЗB)ЗC (ассоциативность З)	2'. AИ(BИC) = (AИB)ИC (ассоциативность И)
3. AЗ(BИC) = (AЗB)И(AЗC) (дистрибутивность З относительно И)	3'. AИ(BЗC) = (AИB)З(AИC) (дистрибутивность И относительно З)
4. AЗЖ = A	4'. AИU = A
5. AЗA = U	5'. AИA = Ж
6. AЗA =A (закон идемпотентности)	6'. AИA = A (закон идемпотентности)
7. AЗU = U	7'. AИЖ = Ж
8. AЗB = AИB (закон де Моргана)	8'. AИB = AЗB (закон де Моргана)
9. AЗ(AИB) = A (закон поглощения)	9'. AИ (AЗB) = A (закон поглощения)

 

Докажем тождество 3. Сначала покажем, что AЗ(BИC) Н (AЗB)И(AЗC). Действительно, если xОAЗ(BИC), то xОA или xОBИC. Если xОA, то xОAЗB и xОAЗC. Следовательно, xО(AЗB)И(AЗC). Если xОBИC, то xОB и xОC. Отсюда xОAЗB и xОAЗC, а значит xО(AЗB)И(AЗC). Теперь покажем, что (AЗB)И(AЗC) Н AЗ(BИC). Если xО (AЗB)И(AЗC), то xОAЗB и xОAЗC. Следовательно, xОA или xОB и xОC, т. е. xОBИC. Отсюда xОAЗ(BИC).

Докажем тождество 8. Пусть xÎAÇB. Тогда xÎU и xÏ AÇB. Следовательно, xÏ A и xÏ B. Отсюда xÎA и xÎB, а значит, xÎAÈB. Итак, AÇB Í AÈB. Пусть теперь, xÎAÈB. Тогда xÎA и xÎB. Следовательно, xÎU и xÏ A и xÏ B. Значит, xÏ AÇB, т. е. xÎAÇB. Итак, AÈB Í AÇB.

Остальные тождества доказываются аналогично. Рекомендуется сделать это самостоятельно. Справедливость этих тождеств можно наглядно проиллюстрировать с помощью диаграмм Венна, но это, конечно, не является доказательством. С другой стороны, диаграмму вполне можно использовать, чтобы на частном примере опровергнуть какое-нибудь общее утверждение.

Теорема 1.2. Предложения о произвольных множествах A и B попарно эквивалентны:

1) AНB; 2) AИB = A; 3) AЗB = B.

Докажем, что из первого предложения следует второе. Действительно, так как AИBН A, то достаточно показать, что в этом случае AН AИB. Но если xОA, то xОB, так как AНB, и, следовательно, xОAИB.

Докажем, что из второго предложения следует третье. Так как AИB = A, то AЗB = (AИB)ЗB. По закону поглощения (см. тождество 9) BЗ(AИB) = B. Отсюда, используя закон коммутативности, получаем AЗB = B.

Докажем, что из третьего предложения следует первое. Так как AН AЗB, а по условию третьего предложения AЗB = B, то AНB.

Отношения

Замечание. Предыдущее определение апеллирует к таким неопределенным понятиям как "совокупность" и "расположенные в определенном… Упорядоченная n-ка элементов x1, x2,…,xn обозначается <x1, x2,…,xn> и,… Математическое понятие "отношение", так же, как и понятие "множество", является очень широким и…

Пример 1 8.

Пусть r и j - отношения на множестве людей A, определенные следующим образом:

x r y, если и только если x - мать y;

x j y, если и только если x - отец y.

Имеем <x,y>Î j л r, тогда и только тогда, когда x - бабушка по линии отца для y. И <x,y>Î r л j, тогда и только тогда, когда x - дедушка по линии матери для y.

Покажем, что композиция отношений является ассоциативной операцией. Пусть даны три отношения r Í A´B, j Í B´C и g Í C´D. Докажем, что (gлj)лr = gл (jлr). Действительно, <a,d>Î(g ë j) ë r ó <a,b>Îr и <b,d> Î g ë j для некоторых bÎB ó <a,b>Îr и <b,c>Î j и <c,d>Î g для некоторых bÎB и cÎC ó <a,c>Î j ë r и <c,d>Î g для некоторых cÎC ó <a,d>Î gë(j ë r ).

Определение.

· Отношение r на множестве X называется рефлексивным, если для любого элемента xОX выполняется xrx.

· Отношение r на множестве X называется симметричным, если для любых x, y О X из xry следует yrx.

· Отношение r на множестве X называется транзитивным, если для любых x, y, z О X из xry и yrz следует xrz.

· Отношение r на множестве X называется антисимметричным, если для любых x, yОX из xry и yrx следует x = y.

 

Пример 1.9.

1. Пусть отношение r задано на множестве действительных чисел R и x r y, если и только если x £ y. Тогда r рефлексивно, потому что x £ x для всех xÎR. Отношение r не симметрично, например, 1£2, но 2 £ 1 не выполнено. Отношение r очевидно является транзитивным, ибо если x £ y и y £ z, то x £ z. Отношение является антисимметричным, поскольку x £ y и y £ x влечет x = y.

2. Пусть r1 = {<1,2>, <2,3>}, r2 = {<1,2>, <1,3>}. Тогда отношение r1 не транзитивно, так как <1,3> Ï r . Но отношение r2 является транзитивным, поскольку нет вообще таких элементов x, y и z, чтобы выполнялось условие xry и yrz.

3. Пусть A - непустое множество и r = Æ (пустое отношение на A). Тогда отношение r является симметричным, транзитивным, антисимметричным. Если же A = Æ, то r еще и рефлексивно.

Функции

Определение. Бинарное отношение f называется функцией, если из <x, y> О f и <x,z> О f следует y = z. Поскольку функции являются бинарными отношениями, то к ним применим… Если f - функция, то вместо <x, y>О f пишут y = f(x) и говорят, что y - значение, соответствующее аргументу x,…

Эквивалентность

Одним из самых важных типов отношений является отношение эквивалентности на множестве. Определение. Рефлексивное, симметричное и транзитивное отношение r на… Пример 1.12.

Пример 1.14.

X = {1, 2, 3, 4, 5}. Тогда {{1, 2}, {3, 5}, {4}} - разбиение множества X. Пусть X - множество студентов института. Тогда разбиением этого множества является, например, совокупность студенческих групп.

Теорема 1.7. Всякое разбиение множества X определяет на X отношение эквивалентности r: xry тогда и только тогда, когда x и y принадлежат одному подмножеству разбиения.

Рефлексивность и симметричность r очевидны. Пусть теперь xry и yrz. Тогда x, y О X₁, y,z О X₂, где X₁ , X₂ - подмножества из разбиения X. Поскольку yОX₁, yОX₂, то X₁ = X₂. Следовательно, x, z О X₁ и xrz.

Теорема 1.8. Всякое отношение эквивалентности r определяет разбиение множества X на классы эквивалентности относительно этого отношения.

Докажем, что совокупность классов эквивалентности определяет разбиение множества X. В силу теоремы 1.6 xО[x], а следовательно, каждый элемент множества X принадлежит некоторому классу эквивалентности. Из теоремы 1.6 вытекает также, что два класса эквивалентности либо не пересекаются, либо совпадают, так как если zО[x] и zО[y], то xrz, откуда [x]=[z], и yrz, откуда [y] = [z]. Следовательно, [x] =[ y].

Определение. Совокупность классов эквивалентности элементов множества X по отношению эквивалентности r называется фактор-множеством множества X по отношению r и обозначается X/r.

Порядок

Элементы многих множеств можно разместить в определенном порядке на основе некоторого, заранее оговоренного соглашения. Например, на любом подмножестве A множества целых положительных чисел можно договориться о таком расположении элементов, при котором меньшие элементы будут находиться левее больших. При этом можно сказать, что на множестве A определено отношение порядка x r y, где r есть отношение "меньше или равно" (x £ y).

Определение. Рефлексивное, транзитивное и антисимметричное отношение называется отношением частичного порядка на множестве X и обозначается символом ‚.

 

Пример 1. 15.

1. Отношение x Ј y на множестве действительных чисел есть отношение частичного порядка.

2. Отношение x < y на множестве действительных чисел не является отношением частичного порядка, поскольку не рефлексивно.

3. Во множестве подмножеств некоторого универсального множества U отношение A Н B есть отношение частичного порядка.

4. Схема организации подчинения в учреждении есть отношение частичного порядка на множестве должностей.

5. Отношение на множестве слов, определенное так: "слово w связано отношением r со словом v, если w = v или w появляется в словаре перед словом v" является отношением частичного порядка (лексикографический порядок).

Определение. Отношение частичного порядка на множестве X, для которого любые два элемента сравнимы, т. е. для любых x, y О X x ‚ y или y ‚ x, называется отношением линейного порядка.

Пример 1.15.В примере 1.14 отношение, определенное в пунктах 1 и 5 есть отношение линейного порядка, а отношение, определенное в п. 2, таковым не является.

Пусть на множестве X задано отношение частичного порядка r. Как можно задать отношение частичного порядка на множестве XґX, т. е. как сравнивать пары элементов из множества X? Один из возможных способов состоит в следующем: на множестве XґX определяем отношение P условием <a, b>P<c, d> у arc и brd. Отношение P есть отношение частичного порядка. Оно называется отношением Парето.

Определение. Множество X с заданным на нем частичным (линейным) порядком называется частично (линейно) упорядоченным.

Логика есть анатомия мышления.

Джон Локк

 

Глава 2. Логика высказываний

 

Было бы крайне нелогично руководствоваться в жизни только логикой.

Лешек Кумор

Зачем мы изучаем математическую логику?

Логика есть наука о законах и формах познающего мышления. Логика изучает мышление, но не всякое мышление, а лишь те мыслительные процессы, которые… Логику интересует лишь форма наших мыслей, но не их содержание. Разнообразие… В этом отношении логика сходна с грамматикой, которую мы изучали в школе. Грамматика тоже исследует и описывает формы…

Высказывания

Мы начинаем изучать математическую логику со сравнительно ограниченного и нетрудного ее раздела, чтобы затем иметь возможность продвигаться вширь и… Под высказыванием принято понимать языковое предложение, о котором имеет смысл… Высказываниями являются, например, следующие предложения: "дважды два - четыре", "лошади едят овес и…

Логические связки

Грамматическими средствами в разговорном языке из нескольких высказываний можно составить сложное (составное) высказывание. Например, с помощью… В математической логике используются специальные операции (конструкции),… Эти логические операции (связки) над высказываниями таковы, что истинностные значения составных высказываний…

Формулы логики высказываний

Мы определим формальный язык для описания логики высказываний. Это описание чисто синтаксическое и оно не требует, чтобы формулы логики высказывания… Алфавитом называется любое непустое множество. Элементы этого множества… Алфавит логики высказываний содержит следующие символы: высказывательные переменные X1, X2,…; логические символы…

Пример 2.3.

1) Таблица 6 - таблица истинности для формулы (X₁ЙX₂)Ъ(X₁Й(X₁&X₂)). Здесь каждая строка содержит некоторое распределение истинностных значений для переменных X₁ и X₂ и соответствующие истинностные значения, принимаемые различными подформулами, которые возникают при построении формулы (X₁ЙX₂)Ъ(X₁Й(X₁&X₂)).

 

Таблица 6

X1	X2	X1ЙX2	X1&X2	X1Й(X1&X2)	(X1ЙX2)Ъ(X1Й(X1&X2))
И	И	И	И	И	И
И	Л	Л	Л	Л	Л
Л	И	И	Л	Л	И
Л	Л	И	Л	И	И

 

 

2) Таблица 7 - таблица истинности для формулы (X₁ЙX₂)ЪШX₃.

 

Таблица 7

X1	X2	X3	ШX3	X1ЙX2	(X1ЙX2)ЪШX3
И	И	И	Л	И	И
И	И	Л	И	И	И
И	Л	И	Л	Л	Л
И	Л	Л	И	Л	И
Л	И	И	Л	И	И
Л	И	Л	И	И	И
Л	Л	И	Л	И	И
Л	Л	Л	И	И	И

 

Если в формуле имеется k различных переменных, то имеем 2^k различных распределений истинностных значений для переменных и, следовательно, истинностная таблица для такой формулы содержит 2^k строк.

Равносильность формул

Пусть A и B - две формулы и {X1, X2,…, Xn} - множество всех высказывательных переменных, входящих в формулу A и/или в формулу B. Будем называть эти… Нужно различать символы ~ и º. Так, ~ является символом формального… Отношение равносильности есть отношение эквивалентности. Действительно, оно рефлексивно, так как для любой формулы A…

Тождественно-истинные формулы

 

Определение.Формула, которая истинна независимо от того, какие значения принимают встречающиеся в ней высказывательные переменные, называется тавтологией (или тождественно-истинной формулой).

Формула является тавтологией тогда и только тогда, когда соответствующая истинностная функция принимает только значение И, или, что тоже, если в ее таблице истинности столбец под самой формулой состоит только из букв И.

Определение.

· Формула называется тождественно-ложной или противоречием, если она ложна независимо от того, какие значения принимают встречающиеся в ней… · Формула называется опровержимой, если при некотором распределении… Приведем утверждения, которые являются очевидными следствиями данных определений:

Нормальные формы формул

Содержание этого параграфа изложим, следуя [24]. Будем рассматривать формулы, содержащие только логические операции &,… Формула A* называется двойственной формуле A, если она получена из A одновременной заменой всех символов &,…

Разрешимость для логики высказываний

Проблемой разрешимости для логики высказываний называют следующую проблему: существует ли алгоритм, который позволил бы для произвольной формулы в… Ясно, что эта проблема разрешима, поскольку всегда можно перебрать все оценки… Теорема 2.6. Формула является тавтологией в том и только том случае, если в ее КНФ в любую из элементарных дизъюнкций…

Глава 3. Булевы алгебры

 

Характерная черта современных компьютеров - сведение всех вычислительных структур (чисел, символов, массивов и т. п.) к двоичным словам и алгоритмам их обработки. С математической точки зрения мы имеем дело с частным случаем булевых алгебр.

 

Аксиома - это истина, на которую не хватило доказательств.

В. Хмурый

Абстрактное определение булевых алгебр

Определение.Множество элементов B с заданным на нем двуместными операциями Ù и Ú (конъюнкцией и дизъюнкцией) и одноместной операцией… fÙg = gÙf, fÚg = gÚf (коммутативность); (fÙg)Ùh = fÙ(gÙh), (fÚg)Úh = fÚ(gÚh) (ассоциативность);

Модель исчисления высказываний

Во второй главе показано, что операции Ú и Ù ассоциативны, коммутативны, и каждая из них дистрибутивна относительно другой. Если мы… Теоретико-множественная модель Пусть A - непустое множество, тогда множество-степень P(A) является моделью булевой алгебры, если условиться о…

Булевы функции. Теорема о нормальной булевой форме

Рассмотрим еще одну модель булевой алгебры. Определение. Пусть M - произвольная булева алгебра с базисными операциями… f: Mn à M

Определение.

Если в двухэлементной булевой алгебре элементы Ë и Î интерпретировать как "включено" и "выключено", то двоичные… Если M = {И, Л} - булева алгебра значений истинности, то булевы функции… Переключательные функции одной переменной имеют вид

Полные системы булевых функций

Определение.Система функций {f1, f2,…, fn} называется полной, если любая булева функция может быть выражена через функции f1, f2,…, fn с помощью… Теорема 3.2. Следующие системы булевых функций полны: {Ø, Ù, Ú}; {Ø, Ú}; {Ø, Ù}; {Ø, É}; {+, Ù, 1};…

Пример 3.2.

XÚYÚZ = XYZ + XY + XZ + YZ + X + Y + Z.

Переключательную функцию из примера 3.1 f(a₁,a₂,a₃) = (a₁Ùa₂Ùa₃) Ú(Øa₁ÙØa₂Ùa₃)Ú(Øa₁Ùa₂ÙØa₃)Ú(a₁ÙØa₂ÙØa₃) можно представить в виде следующего многочлена Жегалкина: a₁a₂+a₁a₃+a₁+a₂+a₃.

Переключательные элементы

    один "выход" (рис. 3). Рис. 3 "Черный ящик" На каждый из входов могут подаваться два сигнала (например, отсутствие электрического тока или наличие его), которые…

Глава 4. Логика предикатов

Формулы логики предикатов

Существуют такие виды логических рассуждений, которые нельзя формализовать на языке логики высказываний. Вот примеры таких рассуждений: 1. Каждый любит сам себя. Значит, кого-то кто-нибудь любит. 2. Ни одно животное не бессмертно. Собаки - животные. Значит некоторые собаки не бессмертны.

Пример 4.1.

1. P(x) º "x делится на 2",

Q(x) º "x делится на 3",

P(x)&Q(x) º "x делится на 6".

2. S(x,y) º "x = y ",

ØS(x,x) É S(x,y) - предикат истинен при любых x и y.

Наряду с применением логических связок с предикатами можно выполнять иоперации квантификации или "связывания квантором переменную".

Определение. Квантор общности.Пусть P(x) - предикат, тогда формула "x P(x) обозначает высказывание, которое истинно тогда и только тогда, когда для всех xÎM предикат P(x) - истинен. "xP(x) читается как "для всех x P(x)". Формула "x P(x) от x не зависит - вместо x нельзя подставить никакую предметную константу. Символ " называется квантором общности или универсальным квантором.

Формула "xP(x) на обычном языке передается также и следующими способами:

P(x) при произвольном x;

P(x), каково бы ни было x;

для каждого x (верно) P(x);

всегда имеет место P(x);

каждый обладает свойством P;

все удовлетворяет P.

Определение. Квантор существования.Пусть P(x) - предикат, тогда формула $x P(x) обозначает высказывание, которое истинно тогда и только тогда, когда найдется такой xÎM, что предикат P(x) - истинен. $x P(x) читается как "существует такой x, что P(x)". Формула $x P(x) от x не зависит - вместо x нельзя подставить никакую предметную константу. Символ $ называется квантором существования или экзистенциальным квантором.

Формула $xP(x) на обычном языке передается также и следующими способами:

для некоторых x (имеет место) P(x);

для подходящего x (верно) P(x);

имеется x, для которого P(x);

у некоторых вещей есть признак P;

кто-нибудь относится к (есть) P.

Пример 4.2.

$ x (P(x)&Q(x)) º "существует x, который делится на 6" - истинное высказывание.

" x (P(x)&Q(x)) º "все x делятся на 6" - ложное высказывание.

Определение. Алфавит языка логики предикатов содержит:

1) символы предметных переменных x, y, z, x₁, y₁, z₁ и т. д.;

2) символы предикатов P, Q, P₁, Q₁ и т. д.;

3) символы логических операций &, Ú, Ø, É, ~;

4) символы кванторов " , $ .

Определение. Слово в алфавите логики предикатов называется формулой, если выполнены следующие условия (одновременно определяются понятия свободной и связанной переменной формулы).

1. P(x₁, x₂, …, x_n) - формула, если P - n-местный предикат (Такая формула называется атомарной). Все переменные x₁, x₂, …, x_n - свободные переменные, связанных переменных в этой формуле нет.

2. Пусть A - формула, тогда ØA - формула с теми же свободными и связанными переменными, что и в формуле A.

3. Пусть A и B - формулы, причем нет таких переменных, которые были бы связаны в одной формуле и свободные - в другой. Тогда (A&B), (AÚB), (AÉB), (A~B) суть формулы, в которых свободные переменные формул A и B остаются свободными, а связанные переменные формул A и B остаются связанными.

4. Пусть A - формула, содержащая свободную переменную x. Тогда "x A, $ x A тоже формулы. Переменная x в них связана. Остальные же переменные, которые в формуле A свободны, остаются свободными. Переменные, которые в формуле A были связаны, остаются связанными. В этих вновь полученных формулах формула A называется областью действия квантора " x и $ x соответственно.

5. Слово в алфавите логики предикатов называется формулой только в том случае, если это следует из правил 1-4.

Пример 4.3.

Следующие выражения являются формулами логики предикатов: P(x₁,x₂,x₇) - атомарная формула, в которой x₁, x₂, x₇ - свободные переменные; (" x $ y P(x, y, z))É" x Q(x, w) -формула, в которой переменные x, y связаны, а переменные z, w свободны.

Выражение ( " x $ y P(x, y, z))É" x Q(x, y) не является формулой.

 

Факты не существуют - есть только интерпретации.

Фридрих Ницше

Интерпретации

Формулы имеют смысл только тогда, когда имеется какая-нибудь интерпретация входящих в нее символов. Определение. Под интерпретацией мы будем понимать всякую пару, состоящую из… Для данной интерпретации всякая формула без свободных переменных представляет собой высказывание, которое истинно или…

Выполнимость и общезначимость

Формула A истинна в данной интерпретации, если она принимает значение И на любом наборе значений своих свободных переменных. Формула A называется ложной в данной интерпретации, если она не является… Формула A общезначима (в логике предикатов), если она истинна в любой интерпретации.

Глава 5. Исчисления

 

Как было сказано выше, в логике предикатов, в отличие от логики высказываний, нет эффективного способа для распознавания общезначимости формул. Выходом из этой неприятной ситуации является следующий подход: выделяем небольшое множество общезначимых формул и указываем правила, с помощью которых из известных общезначимых формул создаются новые общезначимые формулы. Если окажется, что таким образом мы можем получить любую общезначимую формулу, то это нас вполне устроит.

Указанный путь реализуется в рамках так называемых формальных аксиоматических теорий.

Формальные аксиоматические теории

Формальная теория представляет собой множество чисто абстрактных объектов (не связанных с внешним миром), в которой представлены правила… Формальную теорию иногда называют аксиоматикой или формальной аксиоматической… Определение. Формальная теория T считается определенной, если:

Исчисление высказываний

Оказывается множество тавтологий логики высказываний можно описать в рамках простой формальной аксиоматической теории - исчисления высказываний. Определим исчисление высказываний следующим образом: 1. Символы исчисления высказываний: Ø, É, (, ) и буквы Xi с целыми положительными числами в качестве…

Теорема 5.2

2. Любая теорема в исчислении высказываний является тавтологией. Доказательство. То, что каждая аксиома A1-A3 является тавтологией легко… Действительно, пусть при произвольном распределении истинностных значений формулы A и AÉB являются…

Исчисление предикатов

Исчисление предикатов - это аксиоматическая теория, символами которой являются, по существу, те же символы, что и в логике предикатов: 1) символы предметных переменных: x1, x2,…; 2) символы предикатов P, Q, R, A, …;

Теорема 5.4

2. Формула, получающаяся из общезначимых формулы по любому из правил вывода 1-4, является общезначимой. 3. Любая доказуемая в исчислении предикатов формула общезначима.  

Логический вывод

Терпеть не могу логики. Она всегда банальна и нередко убедительна. Оскар Уайльд  

Метод резолюций

Логическое программирование является, пожалуй, наиболее впечатляющим примером применения идей и методов математической логики (точнее, одного из ее… Идея использования языка логики предикатов первого порядка в качестве языка… Первые компьютерные реализации систем автоматического доказательства теорем появились в конце 50-х годов, а в 1965г.…

Применение метода резолюций для ответов на вопросы

Рассмотрим следующий пример из [11]. Предположим, что у нас есть предикат F(x,y), означающий, что x отец y, и истинна следующая формула

F(john,harry) & F(john,sid) & F(sid,liz).

Таким образом, у нас есть три дизъюнкта. Они не содержат переменных или импликаций, а просто представляют базисные факты.

Введем еще три предиката M(x), S(x,y) и B(x,y), означающие соответственно, что x - мужчина, что он единокровен с y, что он брат y. Мы можем записать следующие аксиомы о семейных отношениях:

"x,y (F(x,y) É M(x));

"x,y,w ((F(x,y) & F(x,w)) É S(y,w));

"x,y ((S(x,y) & M(x)) É B(x,y)).

Они утверждают следующее: 1) все отцы - мужчины; 2) если у детей один отец, то они единокровны; 3) брат - это единокровный мужчина.

Пусть мы задали вопрос $z B(z,harry)? Чтобы найти ответ с помощью метода резолюции, мы записываем отрицание вопроса "zØB(z,harry). Затем приводим аксиомы к нормальной форме и записываем каждый дизъюнкт в отдельной строке (так как каждый дизъюнкт истинен сам по себе):

 

ØF(x,y) Ú M(x);	(1)
ØF(x,y) Ú ØF(x,w) Ú S(y,w);	(2)
ØS(x,y) Ú ØM(x) Ú B(x,y);	(3)
F(john,harry);	(4)
F(john,sid);	(5)
F(sid,liz);	(6)
ØB(z,harry).	(7)

Мы не пишем внешних кванторов всеобщности, так как подразумевается, что каждая переменная связана таким квантором.

Для применения резолюции необходимо найти для данной пары дизъюнктов такую подстановку термов вместо переменных, чтобы после нее некоторый литерал одного из дизъюнктов стал отличаться от некоторого литерала другого дизъюнкта лишь отрицанием. Мы можем делать подстановки, так как все переменные связаны кванторами всеобщности. Если, например, мы подставим john вместо x и sid вместо y, то получим следующее:

ØF(john,sid) Ú ØF(john,w) Ú S(sid,w).

Мы можем применить правило резолюции к этому дизъюнкту и к (5), что дает новый дизъюнкт

ØF(john,w) Ú S(sid,w) из (5) и (2) {x->john,y-sid}.

(8)

Продолжая, получим

S(sid,harry) из (4) и (8) {w->harry},	(9)
M(sid) из (6) и (1) {x->sid,y->liz},	(10)
ØS(sid,y) Ú B(sid,y) из (10) и (3) {x->sid},	(11)
B(sid,harry) из (9) и (11) {y->harry},	(12)
пустой дизъюнкт из (12) и (7) {z->sid}.

 

Таким образом, мы вывели дизъюнкт (12), выражающий, что sid брат harry, используя аксиомы и факты (4), (5) и (6). Это противоречит отрицанию нашего вопроса, которое утверждает, что harry не имеет братьев.

Этот пример демонстрирует возможности метода резолюций.

 

У логики один недостаток: она не останавливаться на полпути.

Д. Уиндем "День триффидов".

 

Некоторые вещи недоступны человеческому уму, но мы не знаем какие.

"Закон Джеффи"

 

Неполнота математики

Таким образом, показано, что класс всех теорем исчисления предикатов совпадает с классом общезначимых формул. На этом примере мы видим силу… В 30-годы анонимная группа французских математиков под псевдонимом Никола… В 1889 г. Пеано предложил свои аксиомы для аксиоматизации понятия натурального числа и, после этого была создана…

Глава 6. Теория алгоритмов

Понятие алгоритма и неформальная вычислимость

В этом разделе будет уточнено понятие алгоритма. Кроме того, будут даны строгие математические понятия, которые формализуют представление о том, что… Под алгоритмом понимается способ преобразования представления информации.… Интуитивно говоря, алгоритм - некоторое формальное предписание, действуя согласно которому можно получить решение…

Частично-рекурсивные функции

Определения

Основная идея Гёделя состояла в том, чтобы получить все вычислимые функции из существенно ограниченного множества базисных функций с помощью… Множество исходных функций таково: · постоянная функция 0(x) = 0;

Примеры рекурсивности

Рассмотрим примеры частично-рекурсивных функций. Все эти примеры и много других можно найти в [21, 23].

 

Сложение двух чисел

sum: <x,y> à x+y.

Эта функция является общерекурсивной в силу примитивной рекурсии

sum(x,0) = pr₁(x) = x,

sum(x,y+1) = s(sum(x,y)) = sum(x,y)+1.

 

Умножение двух чисел

prod: <x,y> à x y.

Используем примитивную рекурсию

prod(x,0) = 0(x) = 0,

prod(x,y+1) = sum(prod(x,y),x).

 

Усеченное вычитание 1

d(x) = x-1, если x>0,

d(0) = 0.

Эта функция примитивно-рекурсивна, действительно,

d(0) = 0 = 0(x),

d(y+1) = y = pr₂(<x,y>).

 

Усеченная разность

x¸y = x-y, если x ³ y,

x¸y = 0, если x < y.

Эта функция примитивно-рекурсивна, действительно,

x¸0 = x,

x¸(y+1) = d( x¸y).

 

Модуль разности

|x-y| = x-y, если x³y,

|x-y| = y-x, если x<y.

Эта функция примитивно-рекурсивна в силу суперпозиции

|x-y| = (x¸y)+(y¸x).

 

Факториал

Действительно,

0! = 1,

(y+1)! = prod(y!,y+1).

 

min(x,y) - наименьшее из чисел x и y

В силу суперпозиции: min(x,y) = x¸(x¸y).

 

Знак числа

sg(x) = 0, если x = 0,

sg(x) = 1, если x>1.

В силу рекурсии

sg(0) = 0,

sg(y+1) = 1.

 

rm(x, y) - остаток от деления y на x

В силу рекурсии и суперпозиции

rm(x,0) = 0,

rm(x,y+1) = prod(s(rm(x,y)),sg(|x-s(rm(x,y))|)).

Используя функции, для которых уже установлено, что они являются частично-рекурсивными, мы получаем все новые и новые частично-рекурсивные функции. Существуют критерии, которые позволяют установить частичную рекурсивность сразу для обширных классов функций (см., например, 23, с. 135-151).

Используя минимизацию (m-оператор) можно получать частично-определенные функции из всюду определенных функций. Например, полагая f(x,y) есть частично-рекурсивная функция |x-y²|, мы обнаруживаем, что g(x) = my[f(x,y)=0] - не всюду определенная функция

g(x) = , если x есть точный квадрат и неопределена в противном случае.

Таким образом, тривиально используя m-оператор вместе с суперпозицией и рекурсией, можно построить больше функций, исходя из основных, чем только с помощью суперпозиции и рекурсии (так как эти операции порождают из всюду определенных функций - всюду определенные). Существуют, однако, и общерекурсивные (всюду определенные) функции, для построения которых нельзя обойтись без минимизации. Примером такой функции является функция Аккермана [13, с. 53]:

f(0,y) = y+1,

f(x+1,0) = f(x,1),

f(x+1,y+1) = f(x, f(x+1,y))

 

Чистая математика - это такой предмет, где мы не знаем, о чем мы говорим, и не знаем, истинно ли то, что мы говорим.

Бертран Рассел

Человек должен верить, что непонятное можно понять; иначе он нe стал бы размышлять о нем.

В. Гёте

Ламбда - исчисление

  Ламбда-исчисление было изобретено Алонсом Чёрчем около 1930 г. Чёрч… Ламбда-исчисление - это безтиповая теория, рассматривающая функции как правила, а не как графики. В противоположность…

Пример 6.2.

(lx.ly.y) ((lz. z z) (lz.z z))

® (lx.ly.y) ((lz.z z) (lz.z z))

® (lx.ly.y) ((lz.z z) (lz.z z))

® ...

(бесконечный процесс редукции)

(lx.ly.y) ((lz. z z) (lz.z z))

®ly.y

(редукция закончилась)

 

Порядок редукций (стратегия выбора редексов)

Самым левым редексом называется редекс, символ l которого (или идентификатор примитивной функции в случае d-редекса) текстуально расположен в l-выражении левее всех остальных редексов. (Аналогично определяется самый правый редекс.)

Самым внешним редексом называется редекс, который не содержится внутри никакого другого редекса.

Самым внутреннимредексом называется редекс, не содержащий других редексов.

В контексте функциональных языков и l-исчисления существуют два важных порядка редукций [32].

Аппликативный порядок редукций (АПР), который предписывает вначале преобразовывать самый левый из самых внутренних редексов.

Нормальный порядок редукций (НПР), который предписывает вначале преобразовывать самый левый из самых внешних редексов.

(lx.ly.y) ((lz.zz) (lz.z z)) - самый левый из самых внутренних редексов - вычисление никогда не закончится.

(lx.ly.y) ((lz .z z) (lz .zz)) - самый левый из самых внешних редексов - вычисление закончится за один шаг.

Функция lx.ly.y - это классический пример функции, которая отбрасывает свой аргумент. НПР в таких случаях эффективно откладывает вычисление любых редексов внутри выражения аргумента до тех пор, пока это возможно, в расчете на то, что такое вычисление может оказаться ненужным.

В функциональных языках стратегии НПР соответствуют так называемые ленивые вычисления.“Не делай ничего, пока это не потребуется” - механизмвызова по необходимости (все аргументы передаются функции в не вычисленном виде и вычисляются только тогда, когда в них возникает необходимость внутри тела функции). Clean - один из языков с ленивыми вычислениями.

Стратегия АПР приводит к энергичным вычислениям.“Делай все, что можешь”; другими словами, не надо заботиться о том, пригодится ли, в конечном счете, полученный результат. Таким образом, реализуется механизм вызова по значению (значение аргумента передается в тело функции). В языке Лисп реализуются, как правило, энергичные вычисления.

Следствие из теоремы Чёрча-Россера[7, с.74].Если выражение E может быть приведено двумя различными способами к двум нормальным формам, то эти нормальные формы совпадают или могут быть получены одна из другой с помощью замены связанных переменных.

Теорема стандартизации[7, с. 298-303]. Если выражение E имеет нормальную форму, то НПР гарантирует достижение этой нормальной формы (с точностью до замены связанных переменных).

Рекурсивные функции

Поскольку в l-исчислении все функции анонимны, то для представления рекурсивных функций с помощью ламбда-термов необходимо придумать метод, позволяющий функциям вызывать себя не по имени, а каким-то другим образом.

Представим рекурсивную функцию как функцию, имеющую себя в качестве аргумента. В этом случае функция может оказаться связанной с одной из её собственных переменных и будет, таким образом, содержать в своем теле ссылки на самое себя.

Рассмотрим, например, рекурсивную функцию sum(x), определенную для сложения все целых чисел от 1 до n

sum(n) = (IF (= n 0) 0 (+ n (sum (1- n)))).

В этой записи мы используем пять констант: число 0, булевские функцию для равенства (=), функции для условного выражения (IF), для суммы (+) и для вычитания 1 (1-).

Это выражение может быть представлено в виде l-абстракции, имеющей дополнительный параметр, который при применении этой абстракции связывается с самой функцией. Мы запишем эту промежуточную версию функции sum:

sum = ls . ln . IF (= 0 n) 0 (+ n (s (1- n)))

Все, что нам осталось сделать теперь, - это связать переменную s со значением функции sum, которую пытаемся определить. Это можно сделать, использовав специальную функцию, называемую Y-комбинатором,которая удовлетворяет следующему уравнению:

Y f = f (Y f)

Y также известен как комбинатор неподвижной точки. “Неподвижная точка” функции f - это выражение, которое не изменяется при применении к нему функции f. (Заметим, что функция может иметь несколько неподвижных точек. Например, функция тождества lx . x, имеет бесконечное их число.) Выражение Y f дает наименьшую неподвижную точку функции f .

 

Y sum

= Y(ls . ln . IF (= 0 n) 0 (+ n (s (1- n))))

® (ls . ln . IF (= 0 n) 0 (+ n (s (1- n)))) (Y sum)

® ln . IF (= 0 n) 0 (+ n ((Y sum) (1- n)))

® ln . IF (= 0 n) 0

(+ n ((lm . IF (= 0 m) 0 (+ m ((Y sum) (1- m))))

(1- n))))

 

Данное выражение ведет себя точно так же, как исходное рекурсивное определение sum. Внутреннее вхождение Y sum конструирует копию исходной функции sum, помещая само себя (т. е. Y sum) вместо s в тело копии.

Таким образом, функция sum выражается в l-исчислении в виде

Y(ls . ln . IF (= 0 n) 0 (+ n (s (1- n))))

Проверим:

(Y(ls . ln . IF (= 0 n) 0 (+ n (s (1- n))))) 1

® ln . IF (= 0 n) 0 (+ n ((Y(ls . ln . IF (= 0 n) 0 (+ n (s (1- n)))))

(1- n))) 1

® IF (= 0 1) 0 (+ 1 ((Y(ls . ln . IF (= 0 n) 0 (+ n (s (1- n)))))

(1- 1)))

® (+ 1 ((Y(ls . ln . IF (= 0 n) 0 (+ n (s (1- n))))) 0))

® (+ 1 (ln . IF (= 0 n) 0

(+ n ((Y(ls . ln . ...))))) 0)

® (+ 1 (IF (= 0 0) 0 (+ 0 ((Y (ls . ln . ...))))))

® (+ 1 0)

® 1

 

В общем случае рекурсивная функция f с телом, задаваемым выражением E, записывается в l-исчислении в виде Y (lf . E).

Определим комбинатор неподвижной точки Y следующим образом:

Y = lh . (lx . h ( x x)) (lx . h (x x))

Проверим:

Yf=

(lh . (lx . h ( x x)) (lx . h (x x))) f

® (lx . f ( x x)) (lx . f (x x))

® f ((lx . f (x x)) (lx . f (x x)) )

® f (Y f)

Чистое l-исчисление

Удалив константы и d-правила, мы получаем чистое l-исчисление. В нем можно выразить любые константы и функции. Например, булевы константы и условное выражение можно представить с помощью термов:

TRUE = lx . ly . x

FALSE = lx . ly . y

IF = lp . lq . lr . p q r

Легко проверить, что выполняются следующие редукции:

TRUE A B ® A

FALSE A B ® B

IF TRUE A B =

(lp . lq . lr . p q r) ( lx . ly . x) A B

® (lq . lr . ( lx . ly . x) q r ) A B

® (lq . lr . (ly . q) r ) A B

® (lq . lr . q ) A B

® (lr . A ) B

® A

 

Нумерация Чёрча.Чёрч предложил натуральное число n представлять термом n-кратной композиции (обозначение xⁿ(y) служит сокращением для x(x(...(xy)...)), x повторяется n раз).

Для каждого натурального числа n положим

<0> = lx . ly . y, <n> = lx . ly . xⁿ (y)

 

Тогда сложение чисел определяется ламбда-выражением

+ x y = lp . lq . x p (y p q)

 

Проверим, что это определение удачно.

+ 1 1 = lp . lq . <1> p (<1> p q)

= lp . (lq . ((lx . ly . x y) p ((lx . ly . x y) p q)))

® lp . (lq . ((lx . ly . x y) p p q))

® lp . (lq . (p p q))

= <2>

Говорят, что частичная функция j с k аргументами l-определима термом M, когда

M<n₁><n₂>...<n_k> b-редуцируется к терму <j(n₁,n₂,...,n_k)>, если значение j(n₁,n₂,...,n_k) определено, и

M<n₁><n₂>...<n_k> не имеет нормальной формы, если j(n₁,n₂,...,n_k) не определено.

Теорема Клини [7, с. 189]. Частичная функция частично-рекурсивна тогда и только тогда, когда она l-определима.

Машины Тьюринга

Рассмотрим еще один способ определения вычислимых функций, следуя в изложении [29, стр. 12-14]. Формулировка, выраженная в терминах воображаемой… На неформальном уровне мы можем описывать машину Тьюринга как некий черный… Если мы откроем черный ящик, то обнаружим, что он устроен очень просто. В любой момент времени он может обозревать…

Тезис Чёрча

За последние 60 лет было предложено много различных математических уточнений интуитивного понятия алгоритма. Три из этих подхода мы разобрали.… · Гёдель-Эбран-Клини. Общерекурсивные функции, определенные с помощью… · Пост. Функции, определяемые каноническими дедуктивными системами [13, с. 66-72].

Некоторые алгоритмически неразрешимые проблемы

Определение. Предикат M(x) называется разрешимым, если его характеристическая функция, задаваемая формулой cM(x) = 1, если M(x) истинно; cM(x) = 0, если M(x) ложно

Сложность алгоритмов

Применение математики во многих приложениях, требует как правило, использования различных алгоритмов. Для решения многих задач не трудно придумать… Основные понятия  

Класс E: задачи, экспоненциальные по природе

К экспоненциальным задачам относятся задачи, в которых требуется построить множество всех подмножеств данного множества, все полные подграфы некоторого графа или же все поддеревья некоторого графа.

 

Задачи не попадающие ни в класс P, ни в класс E

На практике существуют задачи, которые заранее не могут быть отнесены ни к одному из рассмотренных выше классов. Хотя в их условиях не содержаться экспоненциальных вычислений, однако для многих из них до сих пор не разработан эффективный (т.е. полиномиальный) алгоритм.

К этому классу относятся следующие задачи [20, с. 207]:

· задача о выполнимости: существует ли для данной булевской формулы, находящейся в КНФ, такое распределение истинностных значений, что она имеет значение И?

· задача коммивояжера;

· решение систем уравнений с целыми переменными;

· составление расписаний, учитывающих определенные условия;

· размещение обслуживающих центров (телефон, телевидение, срочные службы) для максимального числа клиентов при минимальном числе центров;

· оптимальная загрузка емкости (рюкзак, поезд, корабль, самолёт) при наименьшей стоимости;

· оптимальный раскрой (бумага, картон, стальной прокат, отливки), оптимизация маршрутов в воздушном пространстве, инвестиций, станочного парка;

· задача распознавания простого числа; самый лучший в настоящее время тест на простоту имеет сложность порядка O(L(n)^L(L(L(n)))), где L(n) - количество цифр в числе n (выражение L(L(L(n))) стремиться к бесконечности очень медленно; первое число, для которого L(L(L(n))) = 2, равно 10^999999999) [5, стр. 102].

Недетерминированные алгоритмы

 

Мы собираемся более подробно классифицировать задачи, не попадающие ни в класс P, ни в класс E. Для этого вводится понятие недетерминированного алгоритма [26, стр. 443].

Неформально, мы определяем состояние алгоритма как комбинацию адреса выполняемой в текущий момент команды и значений всех переменных. Все алгоритмы, рассматривавшиеся до сих пор были детерминированными; иначе говоря, во всех них для любого данного состояния существует не больше одного вполне определенного "следующего" состояния. Другими словами, детерминированный алгоритм в каждый момент времени может делать только что-либо одно. В недерминированном алгоритме для любого данного состояния может быть больше одного допустимого следующего состояния; другими словами, недетерминированный алгоритм в каждый момент времени может делать больше одной вещи. Недетерминированные алгоритмы не являются в каком-то смысле вероятностными или случайными алгоритмами; они являются алгоритмами, которые могут находиться одновременно во многих состояниях.

Недетерминированность лучше всего понять, рассматривая алгоритм, который производит вычисления до тех пор, пока не доходит до места, в котором должен быть сделан выбор из нескольких альтернатив. Детерминированный алгоритм исследовал бы одну альтернативу, а потом бы возвращался бы для исследования другой альтернативы. Недетерминированный алгоритм может исследовать все возможности одновременно, "копируя", в сущности, самого себя для каждой альтернативы. Все копии работают независимо, не сообщаясь друг с другом каким-либо образом. Эти копии, конечно, могут создавать дальнейшие копии и т. д. Если копия обнаруживает, что она сделала неправильный (или безрезультатный) выбор, она прекращает выполняться. Если копия находит решение, она объявляет о своем успехе, и все копии прекращают работать.

Недетерминированный алгоритм можно моделировать с помощью недетерминированной машины Тьюринга. Машина Тьюринга, которая была введена в §4, является очевидно детерминированной. Обобщим данное там определение, допустив, что каждое значение функции M является множеством троек {<записываемый символ>, <переход>, <номер инструкции>}. Теперь для каждого состояния машины может быть несколько следующих состояний, в соответствии с функцией перехода. И в каждом следующем состоянии запускается новая копия данной машины Тьюринга. Формальное определение недетерминированной машины Тьюринга см. в [6].

Очевидно, никакое физическое устройство не способно на неограниченное недетерминированное поведение; недетерминированные алгоритмы - это абстракция, которая позволяет нам игнорировать некоторые проблемы программирования поиска с возвращением.

Определим NP как класс всех задач, которые можно решить недетерминированными алгоритмами, работающими в течение полиномиального времени, т. е. недетерминированными алгоритмами, в которых всегда есть путь успешного вычисления за время, полиномиальное относительно входа; очевидно, P Í NP. Поскольку путей вычисления может быть экспоненциально много, вероятно, что алгоритмы, допустимые в этом случае, намного сильнее, чем детерминированные алгоритмы, допустимые для задач из P.

Укажем причины, по которым задача коммивояжера попадает в класс NP. С оптимизационными проблемами (такими, например, как задача коммивояжера) связаны соответствующие проблемы распознавания свойств. Такие задачи имеют только два возможных решения - "да" или "нет". Выражаясь абстрактно, проблема распознавания T состоит просто из двух множеств: множества D_T всех возможных частных случаев (индивидуальных задач) и множества Y_T (Y_T ÌD_T) частных случаев с ответом "да".

Задача распознавания, соответствующая задаче о коммивояжере, может быть сформулирована следующим образом.

Условие. Заданы конечное множество C = {c₁, c₂,..., c_m} "городов", "расстояние" d(c_i, c_j) между каждой парой городов c_i, c_j из C и граница B - положительное число.

Вопрос. Существует ли "маршрут", проходящий через все города из C, длина которого не превосходит B? Другими словами, существует ли последовательность <c_k(1), c_k(2),..., c_k(m)> элементов C такая, что

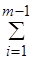d(c_k(i), c_k(i+1))+d(c_k(m), c_k(1)) £ B?

Относительно соответствия между задачами распознавания и задачами оптимизации важно отметить, что задача распознавания не может быть сложней соответствующей задачи оптимизации. Если для задачи о коммивояжере можно за полиномиальное время найти маршрут минимальной длины, то совершенно ясно как за полиномиальное время решить соответствующую задачу распознавания. Для этого только нужно найти маршрут минимальной длины, вычислить его длину и сравнить с заданной границей B.

Полиномиальный алгоритм задачи коммивояжера неизвестен. Предположим, однако, что имеется некоторый маршрут между городами, претендующий на решение задачи распознавания. Нетрудно проверить, является ли этот маршрут полным обходом всех городов, а если это так, то вычислить его длину, сравнить с границей B и тем самым выяснить является ли этот маршрут положительным решением задачи распознавания. Более того, эту "процедуру проверки" можно представить в виде алгоритма, временная сложность которого ограничена в виде полинома от |I|.

Недетерминированный алгоритм, во многих случаях, можно применить для решения задачи распознавания. Такой алгоритм состоит из двух различных стадий - стадии угадывания и стадии проверки. По заданному частному случаю I проблемы T на первой стадии происходит просто угадывание (генерация) некоторой структуры S. Мы можем считать, что для решения задачи запускается одновременно столько копий алгоритма, сколько существует различных структур S. Затем в каждой копии I и S вместе подаются в качестве входа на стадию проверки, которая выполняется обычным детерминированным образом и либо заканчивается ответом "да", либо заканчиваются ответом "нет", либо продолжается бесконечно без остановки (два последних случая можно не различать). Недетерминированный алгоритм "решает" проблему распознавания T, если для каждого частного случая IÎ D_T выполнены следующие два свойства:

1. Если IÎY_T, то существует такая структура S, угадывание которой для входа I приведет к тому, что стадия проверки, начиная работу на входе (I, S), закончится ответом "да".

2. Если IÏ Y_T, то не существует такой структуры S, угадывание которой для входа I обеспечило бы окончание стадии проверки на входе (I, S) ответом "да".

Например, недетерминированный алгоритм решения задачи о коммивояжере можно было бы построить, используя в качестве стадии угадывания просто выбор произвольной последовательности городов, а в качестве стадии проверки упомянутую выше "полиномиальную" процедуру" проверки маршрута. Очевидно, что для любого частного случая I найдется такая догадка S, что результатом работы стадии проверки на входе (I, S) будет "да" в том и только том случае, если для частного случая I существует маршрут искомой длины.

 

NP-трудные и NP-полные задачи

Различные задачи, относящие к классу NP являются эквивалентными относительно некоторого отношения, которое мы сейчас определим. Определение. Задача Q полиномиально сводится к задаче R тогда и только тогда,… · существуют функции g(x) и f(x), вычисляемые за полиномиальное время;

Глава 7. Логические парадоксы

 

Приведем несколько широко известных логических парадоксов. Утверждение A называется парадоксом, если из истинности A следует истинность ØA и из истинности ØA следует истинность A. Тексты этих парадоксов, там где это специально не оговорено, взяты из книги М. Гарднера [9]. Все эти парадоксы являются подлинными в том смысле, что они не содержат явных логических изъянов. Анализ парадоксов привел к различным планам их устранения. Все эти планы предлагают тем или иным путем ограничить "наивные" понятия ("множество", "характеризовать", "истинный", "прилагательное" и т. п.), участвующих в выводе этих парадоксов. [23, стр. 7-10].

Парадокс лжеца

 

По преданию, Эпименид утверждал, что все критяне лжецы. Верно ли это утверждение, если учесть, что сам Эпименид родом с острова Крит?

Другая простейшая форма этого парадокса: истинно ли следующее утверждение в рамочке?

Это утверждение ложно

 

Еще одна форма этого парадокса.

Некто говорит: "Я лгу". Если он при этом лжет, то сказанное им есть ложь, и, следовательно, он не лжет. Если он при этом не лжет, то сказанное им есть истина и, следовательно, он лжет. В любом случае оказывается, что он лжет и не лжет одновременно.

 

Прямое и противоположное утверждения

Это предложение Это предложение не

содержит шесть слов содержит шесть слов

 

Два утверждения в рамочках являются взаимно исключающими утверждения. Значит одно из них истинно, а другое ложно. Какое именно?

Парадокс Платона и Сократа

Платон: Следующее высказывание Сократа будет ложным.

Сократ: То, что сказал Платон, истинно.

 

В связи с парадоксом лжеца может возникнуть мысль, что парадокс возникает, когда утверждение ссылается на свою собственную истинность. Но парадокс Платона и Сократа показывает, что причина лежит глубже.

Парадокс Ришара (1905)[23, стр. 9]

 

С помощью некоторых фраз русского языка могут быть охарактеризованы те или иные вещественные числа. Например, фраза "отношение длины окружности к длине диаметра в круге" характеризует число p. Все фразы русского языка могут быть перенумерованы некоторым стандартным способом, а именно: упорядочим сперва лексикографически (т. е. как в словаре) все фразы, содержащие в точности k букв, а затем поместим все фразы из k букв впереди всех фраз с большим числом букв. Теперь можно перенумеровать все фразы русского языка, которые характеризуют то или иное вещественное число. Для этого достаточно в стандартной нумерации всех фраз опустить все остальные фразы. Число, получающее при такой нумерации номер n, назовем n-ым числом Ришара. Рассмотрим такую фразу: "вещественное число, у которого n-ый десятичный знак равен 1, если у n-го числа Ришара n-ый десятичный знак не равен 1, и n-ый десятичный знак равен 2, если у n-го числа Ришара n-ый десятичный знак равен 1". Эта фраза определяет некоторое число Ришара, допустим k-ое; однако, согласно определение, оно отличается от k-го числа Ришара в k-ом десятичном знаке.

 

Варианты парадокса Б. Рассела

Курт Греллинг(немецкий математик, 1908):

Разделим все прилагательные на два множества: самодескриптивные, обладающие тем свойством, которые они выражают, и несамодескриптивные. Такие прилагательные, как "многосложное", "русское" и "видимое", принадлежат к числу самодескриптивных, а такие прилагательные, как "односложное", "немецкое" и "невидимое", - к числу несамодескриптивных. К какому множеству принадлежит прилагательное "несамодескриптивное"?

Дж. Дж. Берри(библиотекарь оксфордского университета, 1906):

В парадоксе речь идет о "наименьшем целом числе, которое не может быть задано менее чем тринадцатью словами". Выражение, взятое в кавычки, содержит 12 слов. Какому множеству принадлежит определяемое число: множеству целых чисел, которые на русском языке задаются менее чем тринадцатью словами, или множеству целых чисел, задаваемых на русском языке 13 и более словами?

Любой из двух ответов приводит к противоречию.

 

Макс Блэк(философ):

В книге упоминаются различные целые числа. Сосредоточим наше внимание на наименьшем целом числе, которое ни прямо, ни косвенно не упоминается в этой книге. Существует ли такое число?

"Казнь врасплох" [10, с. 96-97]

 

"Преступника приговорили к смертной казне через повешение и поместили его в тюрьму в субботу.

- Тебя повесят в полдень, - сказал ему судья, - в один из семи дней на следующей неделе. Но в какой именно день это должно произойти, ты узнаешь лишь утром в день казни.

Судья славился тем, что всегда держал свое слово. Осужденный вернулся в камеру в сопровождении адвоката. Как только их оставили вдвоем, защитник удовлетворенно ухмыльнулся.

- Неужели не понятно? - воскликнул он. - Ведь приговор судьи нельзя привести в исполнение!

- Как? Ничего не понимаю, - пробормотал узник.

- Сейчас объясню. Очевидно, что в следующую субботу тебя не могут повесить: суббота - последний день недели, и в пятницу днем ты бы уже знал наверняка, что тебя повесят в субботу. Таким образом, о дне казни тебе бы стало известно до официального уведомления в субботу утром, следовательно, приказ судьи был бы нарушен.

- Верно, - согласился заключенный.

- Итак, суббота, безусловно, отпадает, - продолжал адвокат, поэтому пятница становится последним днем, когда тебя смогут повесить. Однако и в пятницу повесить тебя нельзя, ибо после четверга осталось бы всего два дня - пятница и суббота. Поскольку суббота не может быть днем казни, повесить тебя должны лишь в пятницу. Но раз тебе об этом станет известно еще в четверг, то приказ судьи опять будет нарушен. Следовательно, пятница тоже отпадает. Итак, последний день, когда тебя еще могли казнить, это четверг. Однако четверг тоже не годится, потому что, оставшись в среду живым, ты сразу поймешь, что казнь должна состояться в четверг.

- Все понятно! - воскликнул заключенный, воспрянув духом. - Точно так же я могу исключить среду, вторник и понедельник. Остается только завтрашний день. Но завтра меня наверняка не повесят, потому что я знаю об этом уже сегодня.

Итак, безупречными логическими рассуждениями приговоренный убедился в том, что, не нарушив приговора, казнь совершить невозможно. И вдруг, к немалому удивлению осужденного, в четверг утром в камеру является палач. Осужденный, конечно, этого не ждал, но самое удивительное, что приговор оказался совершенно точным - его можно привести в исполнение в полном соответствии с формулировкой".

Парадокс о вычислимых функциях [14, с. 184]

 

Легко доказать, что множество всюду определенных вычислимых функций f: Í à Í является перечислимым, т. е. их можно перенумеровать в виде последовательности f₁, f₂, f₃,... .

Определим теперь новую функцию g формулой

g(n) = f_n(n)+1.

Она не входит в нашу последовательность, поскольку при n=1 она отличается от f₁, при n=2 - от f₂ и т. д. Следовательно, она не вычислима.

С другой стороны, ясно, что она вычислима, так как f_n(n) вычислима, а прибавив 1 к f_n(n), мы получим g(n).

Этот парадокс можно объяснить. На самом деле мы здесь используем две формальные системы. В рамках одной системы (скажем, арифметики), мы описываем вычислимые функции f, а то, что g является вычислимой функцией мы получаем в рамках другой формальной системы, в которой уже используется возможность упорядочить f. Вторая формальная система является надсистемой или метасистемой относительно первой.

 

 

Глава 8. Многозначные логики

 

Двузначная логика предполагает истинность и ложность высказываний («0» или «1»). В многозначных логиках число значений истинности аргументов и функций может быть даже (в общем случае) бесконечным. Обозначим через Nx или Øх-отрицание, Сху или х É у – импликацию, Кху или х Ùу – конъюнкцию, Аху или х Ú у – дизъюнкцию. Значение функции от аргумента а обозначим как [а].

Напомним, что тавтологией называется формула, принимающая значение “истина” (или 1) при любых комбинациях значений входящих в нее переменных. Развитие многозначных логик приводит к тому, что ряд утверждений, являющихся тождественно-истинными в одной логической системе, становятся нетождественно-истинными в другой системе.

Рассмотрим несколько примеров многозначных логик, которые подтверждают это утверждение.

Трехзначная система Я. Лукасевича

  Таблица 11 Х Nx ½ …  

Логика Гейтинга

Из закона исключенного терьего в двузначной логике выводятся: 1. ØØх É х 2. х É ØØх Гейтинг создал трехзначную пропозициональную логику, основываясь на утверждении, что истинным является лишь х É…

Трехзначная система Бочвара Д.А.

Система создавалась Бочваром Д.А. [36] для разрешения парадоксов классической математической логики методом формального доказательства… Создавая свою систему Д.А. Бочвар, разделил высказывания на имеющие смысл… Внутренние функции называются классическими содержательными функциями переменных высказываний, а внешние –…

К - значная логика Поста Е.Л.

Логика Поста [37] является обобщением частного случая – двузначной логики, когда К=2. Действительно, по Посту значения истинности принимают значения…   Таблица 15 X N1x N2x . . . K-1 K . . …

Литература

 

1. Carry H. B., Feys R. Combinatory Logic, vol. I, Amsterdam: North-Hollan3 Co., 1958.

2. Church A. The Calculi of Lambda Conversion. Princeton University Press, Princeton, 1941.

3. Schönfincel M. Über die Bausteine der mathematischen Logik. Math. Annalen, 92, 1924, s. 305-316.

4. Turing A. M. On computable numbers with an application to the Entscheidungs-problem. - Proc. London Math. Soc., Ser. 2, 1936, 42, p. 230-265.

5. Акритас А. Основы компьютерной алгебры с приложениями: пер. с англ. - М.: Мир, 1994. - 544 с.

6. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. М.: Мир, 1979. - 536 с.

7. Барендрегт Х. Ламбда-исчисление. Его синтаксис и семантика. - М.: Мир, 1985.-606с.

8. Де Боно Э. Латеральное мышление - СПб.: Питер Пвблишинг, 1997. - 320с.

9. Гарднер М. А ну-ка, догадайся! М.: Мир, 1984.- 213 с.

10. Гарднер М. Математические досуги: Пер. с англ. - М.: Оникс, 1995.- 496с.

11. Грэй П. Логика, алгебра и базы данных: Пер. с англ.- М.: Машиностроение, 1989. - 359 с.

12. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. - М.: Мир, 1982.

13. Катленд Н. Вычислимость. Введение в теорию рекурсивных функций: Пер. с англ.- М.: Мир, 1983.-256 с.

14. Кац М., Улам С. Математика и логика. Ретроспектива и перспективы: Пер. с англ. - М.: Мир, 1971. - 254 с.

15. Кнут Д. Искусство программирования для ЭВМ.

16. Том 1. Основные алгоритмы. М.: Мир, 1976. - 736 с.

17. Том 2. Получисленные алгоритмы. М.: Мир, 1977. - 724 с.

18 Том 3. Сортировка и поиск. М.: Мир, 1978. - 844 с.

19. Литлвуд Дж. Математическая смесь: Пер. с англ.- М.: Наука, 1990. - 140 с.

20. Лорьер Ж.-Л. Системы искусственного интеллекта - М.: Мир, 1991. - 568с.

21. Манин Ю. И. Вычислимое и невычислимое. - М.: Сов. радио. 1980. - 128 с.

22. Манин Ю. И. Доказуемое и недоказуемое. М.: "Советское радио", 1979.

23. Мендельсон Э. Введение в математическую логику - М.: Наука, 1976.- 320с.

24. Нефедов В. Н., Осипова В. А. Курс дискретной математики.М.,1992.

25. Никифоров А. Книга о логике. М.: "Гнозис", 1996

26. Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практика. Пер. с англ. - М.: Мир, 1980. - 478 с.

27. Смаллиан Р. Как же называется эта книга? М.: Мир, 1981.

28. Смаллиан Р. Принцесса или тигр? М.: Мир, 1985. - 221 с.

29. Справочная книга по математической логике: В 4-х частях/Под ред. Дж. Барвайса. - Ч. III. Теория рекурсии: Пер. с англ.-М.: Наука, 1982.- 360 с.

30. Таранов П. С. Секреты поведения людей: Опыт всемирной энциклопедии жизни людей в законах и примерах. - Симферополь: Таврия, 1997. - 544 с.

31. Успенский В. А. Теорема Гёделя о неполноте - М.: Наука, 1982. - 112 с.

32. Филд А., Харрисон П. Функциональное программирование - М.: Мир, 1993.-637с.

33. Штейнгауз Г. Математический калейдоскоп: Пер. с польского. - М.: Наука, 1981. - 160 с.

34. Lukasiewiczy. Opojeciu mozliewosci.-Ruch Filozofiezny. Lwow. 1920. R.5 №9.

35. Гетманова А.Д. Учебник по логике.2-е изд. - М.: Владос, 1995.-303с.

36. Бочвар Д.А. Об одном трехзначном исчислении и его применении к анализу парадоксов классического расширенного функционального исчисления. //Математический сборник.-1938. Т. 4(46). № 2.

37. Post E.L. Introduction to a General Theory of Elementary Propositions //American Journal of Mathematics. 1921. Vol. 43. № 3.

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО КУРСУ

«МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕОРИЯ АЛГОРИТМОВ»

 

Цели и задачи дисициплины

В результате изучения дисциплины обучаемый должен: уметь находить представление и исследовать свойства булевых и многозначных… иметь навыки использования современной символической логики, построения алгоритмов и анализа их сложности. Построения…

Наименование тем

Введение   История развития математической логики и теории алгоритмов. Математическая логика и основания математики. Теория…

Темы практических занятий

 

Таблицы истинности формул алгебры высказываний. ( 2 часа )

 

Нормальные формы формул. ( 4 часа )

 

Булевы функции. ( 4 часа )

 

Правила вывода в исчислении высказываний. ( 2 часа )

 

Правила вывода в исчислении предикатов. ( 2 часа )

 

Построение машин Тьюринга. ( 2 часа )

 

Алгоритмы Маркова. ( 2 часа )

 

Частично рекурсивные функции. ( 2 часа )

 

Функции сложности. ( 2 часа )

 

Построение машин произвольного доступа. ( 2 часа )

 

Контрольная работа. ( 2 часа )

 

 

Самостоятельная работа

 

№	Наименование работы	Количество час.	Форма контроля
1.	Проработка лекционного материала.		Зачет.
2.	Подготовка к практическим занятиям. Выполнение до- машних заданий.		Опрос на прак. занятиях.
3.	Подготовка к контрольным работам.		Проверка контрольной работы
4.	Изучение тем для самосто- ятельной проработки		Зачет. Конспекты.

 

Всего часов самостоятельной работы - 45 часов.

 

КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО КУРСУ

"МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕОРИЯ АЛГОРИТМОВ"

(Упражнение, друзья, дает больше, чем хорошее (природное) дарование.

Эпихарм

КОНТРОЛЬНАЯ № 1

Вариант 1

1. Найдите множество X, удовлетворяющее следующему условию:

A(AX) = Æ.

2. Равны ли два множества:

{{1,2}, {2,3}} и {1,2,3}?

3. Докажите следующее утверждение: AÌB и BÍC Þ AÌC.

4. Пусть A={0, 1}. Перечислите элементы множеств A², A³.

5. Пусть r и j - бинарные отношения, определенные на некотором множестве. Тогда (j r)^-1 = j^-1 r^-1.

6. Укажите все сюръективные отображения множества A={1,2,3} на множество B={a, b}.

7. Характеристическая функция множества A определяется следующим образом

c_A(x) =

Доказать:

c_AÇB(x) = c_A(x)+c_B(x)- c_A(x) c_B(x);

8. Пусть отношение r определено на множестве N² (N - множество натуральных чисел {1,2,3,…}): <x,y> r <u,v> ó x+v = y +u. Доказать, что r - отношение эквивалентности.

9. Построить линейный порядок: а) на множестве N²; б) на множестве NÇN²Ç…ÇNⁿÇ… = {все конечные последовательности из натуральных чисел}.

10. Если r и j - отношения эквивалентности на X, то rÈj также отношение эквивалентности на X.

 

Вариант 2

 

1. Докажите следующее утверждение: AÌB и BÍC Þ AÌC.

2. Равны ли два множества:

{2,3}, {3.4} и {2,3,4}?

3. Найдите AÇB, AÈB, AB, BA, для

A={1,2,3}, B={2,3,4,5}, U = {0,1,…,9};

4. Определим упорядоченную пару <a,b> как множество {{a}, {a,b}}. Убедимся, что такое формальное теоретико-множественное определение вполне соответствует нашему неформальному определению упорядоченной пары. Для этого достаточно доказать, что для любых элементов <a,b> = <c,d> ó a=c, b=d.

5. Пусть x r y ó x² = y². Определите r^-1, r ë r, r^-1ë r^-1.

6. Найдите все отображения множества A={1,2} в себя, укажите, какие из них инъективные, сюръективные.

7. Характеристическая функция множества A определяется следующим образом

c_A(x) =

Доказать:

(x) = 1- c_A(x);

8. Если r и j - отношения эквивалентности на X, то rÈj также отношение эквивалентности на X.

9. Докажите, что отношение делимости на множестве натуральных чисел N является отношением частичного порядка. Является ли это отношение линейным порядком? Является ли отношением частичного порядка отношение делимости на множестве целых чисел Z?

10. Если r и j - отношения эквивалентности на X, то rÇj - отношение эквивалентности на X ó rÇj = r ë j .

 

Вариант 3

 

1. Вставьте между множествами символ Î или Í так, чтобы получилось истинное высказывание:

{1,2} ? {1,2, {1}, {2}};

2. Равны ли два множества:

{4,5}, {5,6} и {4,5,6}?

3. Найдите AÇB, AÈB, AB, BA, для

A={x | x делится на 2}, B = {x| x делится на 3}, U = N - множество натуральных чисел.

4. Пусть AÍC, BÍC. Докажите, что A´B = (A´C)È(C´B).

5. Пусть r - бинарное отношение на R и e_R = {<x,x>|xÎR}. Доказать, что r = e_R ó r ë j = j ë r = j для любого отношения j на R.

6. Пусть X - конечное множество и отображение f: X à X инъективно. Доказать, что тогда f биективно.

7. Характеристическая функция множества A определяется следующим образом

c_A(x) =

Доказать: c_AB(x) = c_A(x) -c_A(x) c_B(x).

8. Если r и j - отношения эквивалентности на X, то rÇj - отношение эквивалентности на X ó rÇj = r ë j .

9. Докажите, что M = {{1}, {2,5}, {3}, {4,6,7}} - разбиение множества A = {1,2,3,4,5,6,7}. Перечислите все элементы отношения эквивалентности r, соответствующего разбиению M.

10. Если r - частичный порядок на X, то r^-1 также частичный порядок на X.

 

Вариант 4

 

1. Докажите следующее утверждение: AÌB и BÍC Þ AÌC.

2. Доказать, что если конечное множество A содержит n элементов, то множество-степень P(A) содержит 2ⁿ элементов.

3. Докажите, что = 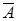Ç B.

4. Докажите, что подмножество C множества A´B является прямым произведением некоторого подмножества A1 множества A и подмножества B1 множества B тогда и только тогда, когда для любых <a,b>ÎC, <c,d>ÎC следует, что <a,d>, <c,b> ÎC.

5. Пусть A={0, 1}. Перечислите элементы множеств A², A³.

6. Характеристическая функция множества A определяется следующим образом

c_A(x) =

Доказать:

c_AÈB(x) = c_A(x) c_B(x);

7. Пусть f: X à Y и AÍX. Образом множества A при отображении f называется множество f(A)= {y | y= f(x), xÎA}.

Пусть BÍY. Прообразом множества B при отображении f называется множество f^-1(B)={xÎX| f(x)ÎB}.

Доказать, что f^-1(AÇB) = f^-1(A)Çf^-1(B).

8. Если r - частичный порядок на X, то r^-1 также частичный порядок на X.

9. Пусть A={1,2,3}. На множестве P(A) задано бинарное отношение X r Y ó "множества X и Y имеют равное количество элементов". Доказать, что это отношение эквивалентности и найдите классы эквивалентности.

10. Докажите, что M = {{1}, {2,5}, {3}, {4,6,7}} - разбиение множества A = {1,2,3,4,5,6,7}. Перечислите все элементы отношения эквивалентности r, соответствующего разбиению M.

 

 

Вариант 5

 

1. Перечислить все элементы каждого из следующих множеств:

{x| xÍ {1}};

2. Доказать, что для любых множеств A и B имеем AÇ(AÈB) = A.

3. Найдите множество X, удовлетворяющее следующему условию:

A(AX) = Æ.

4. Пусть A, B, C, D - непустые множества. Докажите, что

AÍB и CÍD ó A´C Í B´D,

5. Определим упорядоченную пару <a,b> как множество {{a}, {a,b}}. Убедимся, что такое формальное теоретико-множественное определение вполне соответствует нашему неформальному определению упорядоченной пары. Для этого достаточно доказать, что для любых элементов <a,b> = <c,d> ó a=c, b=d.

6. Характеристическая функция множества A определяется следующим образом

c_A(x) =

Доказать:

c_AÇB(x) = c_A(x)+c_B(x)- c_A(x) c_B(x);

7. Пусть A={a₁, a₂,…, a_n} - конечное множество. Определим отображение

f: P(A) à {0,1}ⁿ следующим образом

f(B) = <a₁, a₂,…, a_n>, где a_i=0, если a_iÏB, и a_i=1, если a_iÎB.

Докажите, что f - биекция.

8. Пусть A={1,2,3}. На множестве P(A) задано бинарное отношение X r Y ó "множества X и Y имеют равное количество элементов". Доказать, что это отношение эквивалентности и найдите классы эквивалентности.

9. Если r - частичный порядок на X, то r^-1 также частичный порядок на X.

10. Докажите, что отношение делимости на множестве натуральных чисел N является отношением частичного порядка. Является ли это отношение линейным порядком? Является ли отношением частичного порядка отношение делимости на множестве целых чисел Z?

 

Вариант 6

1. Вставьте между множествами символ Î или Í так, чтобы получилось истинное высказывание: Æ ? {Æ}.

2. Перечислить все элементы каждого из следующих множеств:

{x| xÍ {1}};

3. Найдите соответствующую форму P(x) для каждого множества:

{2,3,5,7,11,13,17,19};

 

4. Пусть A, B, C, D - непустые множества. Докажите, что

A´C = B´D ó A=B и С=В.

5. Пусть AÍC, BÍC. Докажите, что A´B = (A´C)È(C´B).

6. Характеристическая функция множества A определяется следующим образом

c_A(x) =

Доказать:

(x) = 1- c_A(x);

7. Найдите прообраз множества {0} при следующих отображениях R à R:

a) x à sin(x);

b) x à lg(x²+1);

c) x à x²+2x+1.

8. Докажите, что M = {{1}, {2,5}, {3}, {4,6,7}} - разбиение множества A={1,2,3,4,5,6,7}. Перечислите все элементы отношения эквивалентности r, соответствующего разбиению M.

9. Если r и j - отношения эквивалентности на X, то rÇj - отношение эквивалентности на X ó rÇj = r ë j .

10. Построить линейный порядок: а) на множестве N²; б) на множестве NÇN²Ç…ÇNⁿÇ… = {все конечные последовательности из натуральных чисел}.

 

Вариант 7

 

1. Вставьте между множествами символ Î или Í так, чтобы получилось истинное высказывание: Æ ? {{Æ}};

2. Перечислить все элементы каждого из следующих множеств:

{x | xÍ {1,2}};

3. Найдите соответствующую форму P(x) для каждого множества:

{м, о, н, е, ж, т, с, в};

4. Докажите тождество (AB)´C = (A´C)(B´C).

5. Докажите, что подмножество C множества A´B является прямым произведением некоторого подмножества A1 множества A и подмножества B1 множества B тогда и только тогда, когда для любых <a,b>ÎC, <c,d>ÎC следует, что <a,d>, <c,b> ÎC.

6. Характеристическая функция множества A определяется следующим образом

c_A(x) =

Доказать:

c_AB(x) = c_A(x) -c_A(x) c_B(x).

 

7. Какие отображения инъективны, сюръективны?

f: RàR, xà x²+3x+5;

8. Докажите, что отношение делимости на множестве натуральных чисел N является отношением частичного порядка. Является ли это отношение линейным порядком? Является ли отношением частичного порядка отношение делимости на множестве целых чисел Z?

9. Если r и j - отношения эквивалентности на X, то rÈj также отношение эквивалентности на X.

10. Докажите, что M = {{1}, {2,5}, {3}, {4,6,7}} - разбиение множества A={1,2,3,4,5,6,7}. Перечислите все элементы отношения эквивалентности r, соответствующего разбиению M.

 

Вариант 8

 

1. Вставьте между множествами символ Î или Í так, чтобы получилось истинное высказывание: Æ ? {1,2,{1},{Æ}};

2. Перечислить все элементы каждого из следующих множеств:

{x | x Í {1,2,3}};

3. Найдите соответствующую форму P(x) для каждого множества:

[-2,3].

4. Докажите, что (A´B)Ç(C´D) Í (AÇC)´(BÇD).

5. Пусть A, B, C, D - непустые множества. Докажите, что

AÍB и CÍD ó A´C Í B´D,

6. Пусть f: X à Y и AÍX. Образом множества A при отображении f называется множество f(A)= {y | y= f(x), xÎA}.

Пусть BÍY. Прообразом множества B при отображении f называется множество f^-1(B)={xÎX| f(x)ÎB}.

Доказать, что f^-1(AÇB) = f^-1(A)Çf^-1(B).

7. Какие отображения инъективны, сюръективны?

f: RàR, xà x¹⁵(x²-1);

8. Построить линейный порядок: а) на множестве N²; б) на множестве NÇN²Ç…ÇNⁿÇ… = {все конечные последовательности из натуральных чисел}.

9. Пусть отношение r определено на множестве N² (N - множество натуральных чисел {1,2,3,…}): <x,y> r <u,v> ó x+v = y +u. Доказать, что r - отношение эквивалентности.

10. Пусть A={1,2,3}. На множестве P(A) задано бинарное отношение X r Y ó "множества X и Y имеют равное количество элементов". Доказать, что это отношение эквивалентности и найдите классы эквивалентности.

 

Вариант 9

 

1. Вставьте между множествами символ Î или Í так, чтобы получилось истинное высказывание: {1,2} ? {1, 2, {1,2}};

2. Перечислить все элементы каждого из следующих множеств:

{x | x Í Æ}.

3. Приведите пример множеств A, B и C таких, чтобы выполнялись условия AÎB, BÏC, AÍC.

4. Для бинарного отношения r = {<x,y> | x² + y² < 1} найдите D_r и R_r .

5. Докажите тождество (AB)´C = (A´C)(B´C).

6. Пусть A={a₁, a₂,…, a_n} - конечное множество. Определим отображение

f: P(A) à {0,1}ⁿ следующим образом

f(B) = <a₁, a₂,…, a_n>, где a_i=0, если a_iÏB, и a_i=1, если a_iÎB.

Докажите, что f - биекция.

7. Какие отображения инъективны, сюръективны?

f: RàR, xà 2^3x+1;

8. Пусть отношение r определено на множестве N² (N - множество натуральных чисел {1,2,3,…}): <x,y> r <u,v> ó x+v = y +u. Доказать, что r - отношение эквивалентности.

9. Построить линейный порядок: а) на множестве N²; б) на множестве NÇN²Ç…ÇNⁿÇ… = {все конечные последовательности из натуральных чисел}.

10. Если r - частичный порядок на X, то r^-1 также частичный порядок на X.

 

Вариант 10

 

1. Вставьте между множествами символ Î или Í так, чтобы получилось истинное высказывание: {1} ? {1, {1,2}};

2. Перечислите все подмножества множества A:

A = {{1,2}, {3}, 1};

3. Доказать тождество A(BC) = (AB)Ç(AÈC).

4. Пусть A = {1,2,3,4,5}, B = {{1},{1,2},{2,5},{3}}. Для бинарного отношения r = {<a, X> Î A´B| aÎX} найдите D_r и R_r .

5. Докажите, что (A´B)Ç(C´D) Í (AÇC)´(BÇD).

6. Найдите прообраз множества {0} при следующих отображениях R à R:

d) x à sin(x);

e) x à lg(x²+1);

f) x à x²+2x+1.

7. Какие отображения инъективны, сюръективны?

f: Z´Z à Z, <a,b> à a+b, Z - множество целых чисел;

8. Если r и j - отношения эквивалентности на X, то rÈj также отношение эквивалентности на X.

9. Докажите, что отношение делимости на множестве натуральных чисел N является отношением частичного порядка. Является ли это отношение линейным порядком? Является ли отношением частичного порядка отношение делимости на множестве целых чисел Z?

10. Если r и j - отношения эквивалентности на X, то rÇj - отношение эквивалентности на X ó rÇj = r ë j .

 

Вариант 11

 

1. Вставьте между множествами символ Î или Í так, чтобы получилось истинное высказывание: {1,2} ? {1,2, {1}, {2}};

2. Перечислите все подмножества множества A:

A={{1}, {2}, 1};

3. Равны ли два множества:

{{1,2}, {2,3}} и {1,2,3}?

4. Какими свойствами обладает отношение x r y ó x² + x = y² +y, определенное на множестве действительных чисел?

5. Для бинарного отношения r = {<x,y> | x² + y² < 1} найдите D_r и R_r .

6. Какие отображения инъективны, сюръективны?

f: RàR, xà x²+3x+5;

7. Какие отображения инъективны, сюръективны?

f: Zà Z´Z, aà<a,a>;

8. Если r и j - отношения эквивалентности на X, то rÇj - отношение эквивалентности на X ó rÇj = r ë j .

9. Докажите, что M = {{1}, {2,5}, {3}, {4,6,7}} - разбиение множества A={1,2,3,4,5,6,7}. Перечислите все элементы отношения эквивалентности r, соответствующего разбиению M.

10. Построить линейный порядок: а) на множестве N²; б) на множестве NÇN²Ç…ÇNⁿÇ… = {все конечные последовательности из натуральных чисел}.

 

Вариант 12

 

1. Перечислить все элементы каждого из следующих множеств:

{x | x Í Æ}.

2. Перечислите все подмножества множества A:

A = {Æ, {Æ}, {Æ, {Æ}}}.

3. Равны ли два множества:

{2,3},{3.4} и {2,3,4}?

4. Какими свойствами обладает отношение r, определенное на множестве

всех прямых плоскости: x r y ó x пересекается с y?

5. Пусть A={0, 1}. Перечислите элементы множеств A², A³.

6. Какие отображения инъективны, сюръективны?

f: RàR, xà x¹⁵(x²-1);

7.Укажите все сюръективные отображения множества A={1,2,3} на множество B={a,b}.

8. Если r - частичный порядок на X, то r^-1 также частичный порядок на X.

9. Пусть A={1,2,3}. На множестве P(A) задано бинарное отношение X r Y ó "множества X и Y имеют равное количество элементов". Доказать, что это отношение эквивалентности и найдите классы эквивалентности.

10. Если r и j - отношения эквивалентности на X, то rÈj также отношение эквивалентности на X.

 

Вариант 13

 

1. Перечислить все элементы каждого из следующих множеств:

{x | x Í {1,2,3}};

2. Вставьте между множествами символ Î или Í так, чтобы получилось истинное высказывание: {1,2} ? {1,2, {1}, {2}};

3. Равны ли два множества:

{4,5}, {5,6} и {4,5,6}?

4. Какими свойствами обладает отношение r, определенное на множестве

всех прямых плоскости: x r y ó x не пересекается с y?

5. Определим упорядоченную пару <a,b> как множество {{a}, {a,b}}. Убедимся, что такое формальное теоретико-множественное определение вполне соответствует нашему неформальному определению упорядоченной пары. Для этого достаточно доказать, что для любых элементов <a,b> = <c,d> ó a=c, b=d.

6. Какие отображения инъективны, сюръективны?

f: RàR, xà 2^3x+1;

7. Найдите все отображения множества A={1,2} в себя, укажите, какие из них инъективные, сюръективные.

8. Пусть A={1,2,3}. На множестве P(A) задано бинарное отношение X r Y ó "множества X и Y имеют равное количество элементов". Доказать, что это отношение эквивалентности и найдите классы эквивалентности.

9. Построить линейный порядок: а) на множестве N²; б) на множестве NÇN²Ç…ÇNⁿÇ… = {все конечные последовательности из натуральных чисел}.

10. Пусть отношение r определено на множестве N² (N - множество натуральных чисел {1,2,3,…}): <x,y> r <u,v> ó x+v = y +u. Доказать, что r - отношение эквивалентности.

 

 

Вариант 14

 

1. Перечислить все элементы каждого из следующих множеств:

{x | xÍ {1,2}};

2. Вставьте между множествами символ Î или Í так, чтобы получилось истинное высказывание: {1} ? {1, {1,2}};

3. Доказать, что если конечное множество A содержит n элементов, то множество-степень P(A) содержит 2ⁿ элементов.

4. Пусть r - отношение на множестве X. Докажите:

r симметрично ó r^-1 = r ;

5. Пусть AÍC, BÍC. Докажите, что A´B = (A´C)È(C´B).

6. Какие отображения инъективны, сюръективны?

f: Z´Z à Z, <a,b> à a+b, Z - множество целых чисел;

7. Пусть X - конечное множество и отображение f: X à X инъективно. Доказать, что тогда f биективно.

8. Докажите, что M = {{1}, {2,5}, {3}, {4,6,7}} - разбиение множества A={1,2,3,4,5,6,7}. Перечислите все элементы отношения эквивалентности r, соответствующего разбиению M.

9. Докажите, что отношение делимости на множестве натуральных чисел N является отношением частичного порядка. Является ли это отношение линейным порядком? Является ли отношением частичного порядка отношение делимости на множестве целых чисел Z?

10. Если r и j - отношения эквивалентности на X, то rÇj - отношение эквивалентности на X ó rÇj = r ë j .

 

Вариант 15

 

1. Перечислить все элементы каждого из следующих множеств:

{x| xÍ {1}};

2. Вставьте между множествами символ Î или Í так, чтобы получилось истинное высказывание: {1,2} ? {1, 2, {1,2}};

3. Доказать, что для любых множеств A и B имеем AÇ(AÈB) = A.

4. Пусть r - отношение на множестве X. Докажите:

r транзитивно ó r ë r Í r ;

5. Докажите, что подмножество C множества A´B является прямым произведением некоторого подмножества A1 множества A и подмножества B1 множества B тогда и только тогда, когда для любых <a,b>ÎC, <c,d>ÎC следует, что <a,d>, <c,b> ÎC.

6. Какие отображения инъективны, сюръективны?

f: Zà Z´Z, aà<a,a>;

7. Характеристическая функция множества A определяется следующим образом

c_A(x) =

Доказать:

c_AÈB(x) = c_A(x) c_B(x);

8. Докажите, что отношение делимости на множестве натуральных чисел N является отношением частичного порядка. Является ли это отношение линейным порядком? Является ли отношением частичного порядка отношение делимости на множестве целых чисел Z?

9. Докажите, что M = {{1}, {2,5}, {3}, {4,6,7}} - разбиение множества A={1,2,3,4,5,6,7}. Перечислите все элементы отношения эквивалентности r, соответствующего разбиению M.

10. Если r - частичный порядок на X, то r^-1 также частичный порядок на X.

 

Вариант 16

 

1. Доказать, что для любых множеств A и B имеем AÇ(AÈB) = A.

2. Вставьте между множествами символ Î или Í так, чтобы получилось истинное высказывание: Æ ? {1,2,{1},{Æ}};

3. Перечислить все элементы каждого из следующих множеств:

{x| xÍ {1}};

4. Пусть r - отношение на множестве X. Докажите:

r рефлексивно Þ r Í r ë r ;

5. Пусть A, B, C, D - непустые множества. Докажите, что

AÍB и CÍD ó A´C Í B´D,

6. Какие отображения инъективны, сюръективны?

f: P(A) à N, f(X)= количество элементов в X, N - множество

неотрицательных целых чисел, A - конечное множество.

7. Характеристическая функция множества A определяется следующим образом

c_A(x) =

Доказать:

c_AÇB(x) = c_A(x)+c_B(x)- c_A(x) c_B(x);

8. Построить линейный порядок: а) на множестве N²; б) на множестве NÇN²Ç…ÇNⁿÇ… = {все конечные последовательности из натуральных чисел}.

9. Пусть A={1,2,3}. На множестве P(A) задано бинарное отношение X r Y ó "множества X и Y имеют равное количество элементов". Доказать, что это отношение эквивалентности и найдите классы эквивалентности.

10. Докажите, что M = {{1}, {2,5}, {3}, {4,6,7}} - разбиение множества A={1,2,3,4,5,6,7}. Перечислите все элементы отношения эквивалентности r, соответствующего разбиению M.

 

Вариант 17

 

1. Доказать, что если конечное множество A содержит n элементов, то множество-степень P(A) содержит 2ⁿ элементов.

2. Вставьте между множествами символ Î или Í так, чтобы получилось истинное высказывание: Æ ? {{Æ}};

3. Перечислите все подмножества множества A:

A = {{1,2}, {3}, 1};

4. Пусть r - отношение на множестве X. Докажите:

r рефлексивно и транзитивно Þ r = r ë r.

5. Пусть A, B, C, D - непустые множества. Докажите, что

A´C = B´D ó A=B и С=В.

6.Укажите все сюръективные отображения множества A={1,2,3} на множество B={a,b}.

7. Характеристическая функция множества A определяется следующим образом

c_A(x) =

Доказать:

(x) = 1- c_A(x);

8. Пусть отношение r определено на множестве N² (N - множество натуральных чисел {1,2,3,…}): <x,y> r <u,v> ó x+v = y +u. Доказать, что r - отношение эквивалентности.

9. Если r - частичный порядок на X, то r^-1 также частичный порядок на X.

10. Построить линейный порядок: а) на множестве N²; б) на множестве NÇN²Ç…ÇNⁿÇ… = {все конечные последовательности из натуральных чисел}.

 

Вариант 18

 

1. Равны ли два множества:

{4,5}, {5,6} и {4,5,6}?

2. Вставьте между множествами символ Î или Í так, чтобы получилось истинное высказывание: Æ ? {Æ}.

3. Перечислить все элементы каждого из следующих множеств:

{x | x Í Æ}.

4. Какова характеристическая особенность декартовой диаграммы рефлексивного (симметричного, антисимметричного) отношения, определенного на множестве вещественных чисел R.

5. Докажите тождество (AB)´C = (A´C)(B´C).

6. Найдите все отображения множества A={1,2} в себя, укажите, какие из них инъективные, сюръективные.

7. Характеристическая функция множества A определяется следующим образом

c_A(x) =

Доказать:

c_AB(x) = c_A(x) -c_A(x) c_B(x).

8. Если r и j - отношения эквивалентности на X, то rÈj также отношение эквивалентности на X.

9. Если r и j - отношения эквивалентности на X, то rÇj - отношение эквивалентности на X ó rÇj = r ë j.

10. Докажите, что отношение делимости на множестве натуральных чисел N является отношением частичного порядка. Является ли это отношение линейным порядком? Является ли отношением частичного порядка отношение делимости на множестве целых чисел Z?

 

Вариант 19

 

1. Равны ли два множества:

{2,3},{3.4} и {2,3,4}?

2. Докажите следующее утверждение: AÌB и BÍC Þ AÌC.

3.Найдите множество X, удовлетворяющее следующему условию:

A(AX) = Æ.

4. Пусть r₁ = {<x,y>ÎR´R | x‰y >0}, r₂ = {<x,y>ÎR´R | x+y -целое число}. Найти r₁ë r₂.

5. Докажите, что (A´B)Ç(C´D) Í (AÇC)´(BÇD).

6. Пусть X - конечное множество и отображение f: X à X инъективно. Доказать, что тогда f биективно.

7. Пусть f: X à Y и AÍX. Образом множества A при отображении f называется множество f(A)= {y | y= f(x), xÎA}.

Пусть BÍY. Прообразом множества B при отображении f называется множество f^-1(B)={xÎX| f(x)ÎB}.

Доказать, что f^-1(AÇB) = f^-1(A)Çf^-1(B).

8. Если r и j - отношения эквивалентности на X, то rÇj - отношение эквивалентности на X ó rÇj = r ë j.

9. Если r и j - отношения эквивалентности на X, то rÈj также отношение эквивалентности на X.

10. Пусть A={1,2,3}. На множестве P(A) задано бинарное отношение X r Y ó "множества X и Y имеют равное количество элементов". Доказать, что это отношение эквивалентности и найдите классы эквивалентности.

 

Вариант 20

 

1. Равны ли два множества:

{{1,2}, {2,3}} и {1,2,3}?

2. Найдите AÇB, AÈB, AB, BA, для

A={1,2,3}, B={2,3,4,5}, U = {0,1,…,9};

3. Приведите пример множеств A, B и C таких, чтобы выполнялись условия AÎB, BÏC, AÍC.

4. Пусть r₁ = {<x,y>ÎR´R | x‰y >0}, r₂ = {<x,y>ÎR´R | x=y² }. Найти r₁ë r₂.

5. Для бинарного отношения r = {<x,y> | x² + y² < 1} найдите D_r и R_r .

6. Характеристическая функция множества A определяется следующим образом

c_A(x) =

Доказать:

c_AÈB(x) = c_A(x) c_B(x);

7.Какие отображения инъективны, сюръективны?

f: RàR, xà x²+3x+5;

8. Если r - частичный порядок на X, то r^-1 также частичный порядок на X.

9. Пусть отношение r определено на множестве N² (N - множество натуральных чисел {1,2,3,…}): <x,y> r <u,v> ó x+v = y +u. Доказать, что r - отношение эквивалентности.

10. Докажите, что M = {{1}, {2,5}, {3}, {4,6,7}} - разбиение множества A={1,2,3,4,5,6,7}. Перечислите все элементы отношения эквивалентности r, соответствующего разбиению M.

 

 

КОНТРОЛЬНАЯ № 2

  1. Записать составные высказывания в виде формул, употребляя высказывательные… "Для того, чтобы x было нечетным, достаточно, чтобы x было простым";

Содержание

 

 

Авторское предисловие …………………………………………………..
Глава 1. Основы теории множеств …………………………….
§1 Начальные понятия теории множеств ………………………….
§2 Операции над множествами. Диаграммы Венна ………………
§3 Отношения ……………………………………………………….
§4 Функции ………………………………………………………….
§5 Эквивалентность ………………………………………………...
§6 Порядок …………………………………………………………..
Глава 2. Логика высказываний …………………………………
§1 Зачем мы изучаем математическую логику? …………………..
§2 Высказывания ……………………………………………………
§3. Логические связки ………………………………………………
§4 Формулы логики высказываний ………………………………..
§5 Равносильность формул ………………………………………...
§6 Тождественно-истинные формулы ……………………………..
§7 Нормальные формы формул ……………………………………
§8 Разрешимость для логики высказываний ……………………...
Глава 3. Булевы алгебры ……………………………………………
§1 Абстрактное определение булевой алгебры …………………...
§2 Булевы функции. Теорема о нормальной булевой форме …….
§3 Полные системы булевых функций ……………………………
§4 Переключательные элементы …………………………………..
Глава 4. Логика предикатов ………………………………………
§1 Формулы логики предикатов …………………………………...
§2 Интерпретации …………………………………………………..
§3 Выполнимость и общезначимость ……………………………..
Глава 5. Исчисления …………………………………………………
§1 Формальные аксиоматические теории …………………………
§2 Исчисление высказываний ……………………………………...
§3 Исчисление предикатов …………………………………………
§4 Логический вывод ……………………………………………….
§5 Метод резолюций ………………………………………………..
§6 Неполнота математики ………………………………………….
Глава 6. Теория алгоритмов ………………………………………
§1 Понятие алгоритма и неформальная вычислимость …………..
§2 Частично-рекурсивные функции ……………………………….
§3 Ламбда-исчисление ……………………………………………...
§4 Машины Тьюринга ………………………………………………
§5 Тезис Чёрча ………………………………………………………
§6 Некоторые алгоритмически неразрешимые проблемы ……….
§7 Сложность алгоритмов ………………………………………….
Глава 7. Логические парадоксы ………………………………...
Глава 8. Многозначные логики ………………………………….
§1. Трехзначная система Я.Лукасевича …………………………...
§2. Логика Гейтинга ………………………………………………...
§3. Трехзначная система Бочвара Д.А. …………………………….
§4. К-значная логика Поста Е.П. …………………………………...
Литература ………………………………………………………………...
Методические указания по курсу "Математическая логика и теория алгоритмов" ……………………………………………………………….
Котрольные задания по курсу "Математическая логика и теория алгоритмов" ……………………………………………………………….
Контрольная работа №1 ………………………………………………….
Контрольная работа №2 ………………………………………………….