Гривень

Звідки	Куди
2	3	4	5	6	7	8
1
2
3
4
5
6
7

Потрібно визначити найекономічніший маршрут перевезення вантажу.

Побудова графа транспортної мережі. Для розв’язування задачі про визначення найекономічнішого маршруту наявну транспортну мережу доцільно подати у вигляді орієнтованого графа. У нашому прикладі граф міститиме 8 вершин, з яких вершина 1 є початковою, вершина 8 – кінцевою, решта 6 вершин – проміжні. Кількість дуг графа відповідає кількості незафарбованих клітинок таблиці 7.1 – таких клітинок 11. Перерахуємо усі дуги:

(1, 2), (1, 3), (1, 4), (2, 5), (3, 6), (4, 5), (4, 6), (4, 8), (5, 7), (6, 8) та (7, 8).

Довжина кожної дуги є відомою – вона відповідає витратам на перевезення вантажу на відповідній ділянці транспортної мережі.

Отже, граф транспортної мережі матиме вигляд, як це показано на рисунку 7.1, де над кожною дугою вказано її довжину. Потрібно знайти найкоротший шлях від вершини 1 до вершини 8.

 

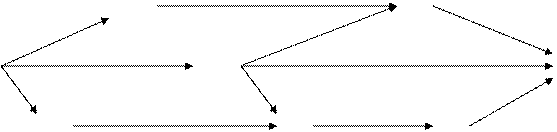
Рис. 7.1. Граф транспортної мережі

 

Формалізація задачі (загальний випадок). Нехай маємо граф транспортної мережі, який містить 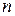вершин, позначених натуральними числами від 1 до 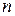, та множину дуг, позначену через . Кожна наявна у графі дуга 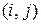означає, що від пункту 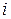до пункту 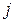існує безпосереднє транспортне сполучення. Відома довжина кожної такої дуги.

Вершина 1 є початковою, вершина 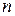– кінцевою, вершини з номерами від 2 до 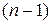– проміжні. Потрібно визначити найкоротший шлях від вершини 1 до вершини .

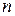Простий спосіб формалізації задачі полягає у такому. Вважатимемо, що у початковій вершині міститься вантаж у кількості 1. Цей вантаж потрібно доставити до кінцевої вершини .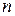

Уведемо змінні 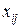, які показуватимуть кількість вантажу, що перевозитиметься безпосередньо з пункту 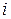до пункту, .

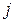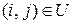Обсяги перевезень повинні задовольняти такі обмеження:

1) з початкової вершини весь вантаж потрібно вивезти:

(7.1)

2) в кожній 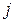-й проміжній вершині весь вантаж, який до неї надходить, потрібно відправити далі:

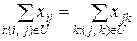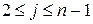, (7.2)

3) весь вантаж потрібно завезти до кінцевої вершини:

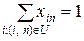(7.3)

4) вантаж є неподільним:

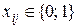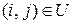, (7.4)

Позначимо через 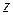загальні витрати на перевезення вантажу, тобто довжину шляху від вершини 1 до вершини 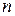. Тоді цільова функція задачі про визначення найекономічнішого маршруту матиме вигляд:

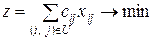(7.5)

Задача (7.1) – (7.5) математично є задачею лінійного програмування з логічними змінними.

Оскільки задачі з логічними або цілочисловими змінними розв’язувати складніше, аніж задачі з неперервними змінними, візьмемо до уваги, що обмеження є надлишковими, а вимоги цілочисловості цих змінних виконуватимуться автоматично, якщо задачу (7.1) – (7.5) звести до транспортної та розв’язувати за методом потенціалів.

Зведення задачі до транспортної полягає, зокрема, у поданні плану перевезень повною квадратною матрицею 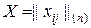та забороною перевезень за фіктивними маршрутами 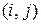, відсутніми на графі транспортної мережі. Ввести цю заборону можна або покладанням вартості перевезень за фіктивними маршрутами надзвичайно великому числу, як це було зроблено у підрозділі 6.3, або явно – введенням відповідних обмежень на усі фіктивні перевезення:

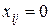для всіх 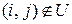(7.6)

Якщо оптимальний план задачі лінійного програмування (7.1), (7.2), (7.3), (7.5) і (7.6) з додатковою вимогою невід’ємності змінних міститиме лише цілочислові (0 або 1) компоненти, задачу визначення найекономічнішого маршруту буде розв’язано. У супротивному випадку, коли після серії запусків інструменту "Поиск решения" серед компонентів оптимального плану лишатимуться дробові, залишається спробувати запустити цей інструмент з явною вказівкою щодо цілочисловості основних змінних задачі.

Необхідною і достатньою умовою існування розв’язку задачі про визначення найекономічнішого маршруту є наявність на графі транспортної мережі принаймні одного маршруту, який з’єднував би початкову вершину з кінцевою. Для перевірки цієї умови часто досить обмежитися візуальним аналізом графа транспортної мережі.

Розв’язування задачі про визначення найдешевшого транспортного маршруту на комп’ютері. Опрацюємо задачу з вихідними даними, наведеними у таблиці 7.1. Відкриємо робочу книгу Excel "Marshrut.xls" та у клітинках A1:H1 (об'єднуємо їх) впишемо назву задачі: "Визначення найдешевшого маршруту".

Блок клітинок A3:H12 відведемо для вихідних даних з таблиці 7.1. Зафарбовані клітинки відповідають випадкам, коли безпосереднє транспортне сполучення від пункту 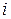до пункту 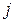відсутнє. Раніше (підрозділ 6.3) в такі клітинки ми заносили значно велике число. Зараз скористаємося іншим способом. Залишимо ці клітинки незаповненими (Excel сприйматиме незаповнену клітинку як клітинку з нульовим значенням), але потім в обмеженнях вимагатимемо, щоб обсяги перевезень на відповідних ділянках транспортної мережі дорівнювали нулю.

Для інформації про план перевезень відведемо блок клітинок A14:H23. Звертаємо увагу, що до початкової вершини 1 не входить жодна дуга, а з кінцевої вершини 8 не виходить жодна дуга (рис. 7.1). Тому для відбиття плану перевезень замість повної квадратної матриці можна з цієї матриці відкинути перший стовпчик та восьмий рядок. Отже, за формою інформаційний блок A14:H23 є копією блоку A3:H12. Значення змінних – про обсяги перевезень за окремими маршрутами – міститимуться у клітинках B17:H23.

Стовпчик I17:I23 відведемо для підсумовування елементів відповідного рядка від колонок B до H включно. Знайдені у цих клітинках за допомогою функцій підсумовування значення відповідатимуть: у клітинці I17 – лівій частині обмеження (7.1); у клітинках I18: I23 – правим частинам обмежень (7.2).

Рядок B24:H24 теж відведемо для допоміжних сум елементів відповідного стовпчика у рядках з 17-го по 23-й. Тоді у клітинках B24:G24 значення відповідатимуть лівим частинам обмежень (7.2), а в клітинці H24 – лівій частині обмеження (7.3).

У клітинках A26:C26 створимо інформаційний блок про загальні витрати. Для цього об’єднаємо клітинки A26:B26 та зафіксуємо в них назву цільового показника: "Загальні витрати", а в клітинку C26 впишемо формулу для його обчислення:

=СУММПРОИЗВ(B6:H12;B17:H23)

Підготовку робочого аркушу закінчено.

Далі в меню “Сервис” оберемо команду “Поиск решения” та в полі “Установить целевую ячейку” діалогового вікна інструменту пошуку рішення вкажемо на адресу цільової клітинки: $C$26.

Перемикач вибору оптимізаційного спрямування цільової функції ввімкнемо у положення “минимальному значению”.

У полі “Изменяя ячейки” вкажемо на адреси клітинок із усіма змінними, які відповідають обсягам перевезень: $B$17:$H$23.

Потім вводитимемо обмеження задачі. Натискуючи кнопку “Добавить”, послідовно вноситимемо:

а) основні обмеження, що відповідають вимогам (7.1), (7.2), (7.3):

$I$17

=

 

$I$18:$I$23

=

$B$24:$G$24

 

$H$24

=

 

б) допоміжні обмеження, згідно вимог (7.6) – потрібно занулити значення змінних, що відповідають обсягам перевезень за фіктивними маршрутами. Вони містяться у зафарбованих клітинках B18:D23, E17:H17, F18:H18, E19, G19:H19, G20, E21:F23, H21 та G22:G23.

Далі зазначимо параметри пошуку рішення: “Линейная модель”, “Неотрицательные переменные” та послідовно натиснемо кнопки "OK" і “Выполнить”.

У вікні “Результаты поиска решения” увімкнемо перемикач “Сохранить найденное решение” та натиснемо ОК.

 

	A	B	C	D	E	F	G	H	I
	Визначення найдешевшого маршруту
	Витрати на перевезення на окремих ділянках
	Звідки	Куди
	План перевезень
	Звідки	Куди
								Разом
									1
									0
									0
									1
									0
									0
									0
	Разом	0	0	1	0	0	0	1
	Загальні витрати

 

Рис. 7.2. Результати розв’язування задачі про визначення
найекономічнішого транспортного маршруту з пункту 1 до пункту 8

Розв’язок задачі показано на рисунку 7.2. Найекономічніший маршрут складається з дуг (1, 4) та (4, 8). Витрати на перевезення вантажу з пункту 1 до пункту 8 за цим маршрутом є мінімально можливими, вони дорівнюють 110 грн., про що засвідчує значення у клітинці C26.

 

7.2. Визначення максимального потоку від одного до іншого
несуміжних пунктів транспортної мережі

 

Постановка та економіко–математична модель задачі. Нехай маємо граф транспортної мережі, який містить 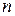вершин, позначених натуральними числами від 1 до 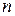, та множину дуг, позначену через 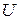. Вершина 1 є початковою, вершина 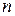– кінцевою. Інші вершини – проміжні. Кожна наявна у графі дуга 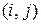означає, що від пункту 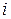до пункту 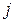існує безпосереднє транспортне сполучення. Відома пропускна спроможність 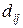кожної такої дуги. Із пункту 1 деяка продукція починає усіма можливими маршрутами перевозитися до пункту 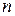, утворюючи так званий потік. Потрібно, враховуючи топологію транспортної мережі та пропускні спроможності кожної ділянки мережі, визначити максимально можливий розмір такого потоку.

Позначимо через 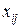обсяг продукції, що перевозитиметься безпосередньо з пункту 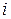до пункту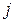, , 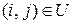через 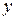– розмір потоку продукції, та перейдемо до побудови економіко–математичної моделі.

Цільова функція відбиватиме вимогу максимізації розміру потоку:

(7.7)

Обмеження задачі враховують наступні вимоги:

1) спочатку весь потік міститься у вершині 1, з якої всю продукцію потрібно вивезти:

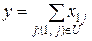(7.8)

2) в кожній 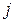-й проміжній вершині вся продукція, яка до неї надходить, має бути відправленою далі:

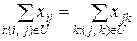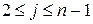, (7.9)

3) весь потік продукції повинен надійти до кінцевої вершини:

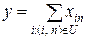(7.10)

4) на кожній з дуг обсяги перевезень невід’ємні та обмежені пропускними спроможностями цих дуг:

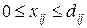, (7.11)

Модель (7.7) – (7.11) є задачею лінійного програмування. Необхідною умовою існування її розв’язку є наявність на графі транспортної мережі принаймні одного маршруту від початкової до кінцевої вершини. Достатньою – додатково – наявність у графі принаймні одного перерізу, всі дуги якого мають обмежені пропускні спроможності. /Перерізом графа називається така підмножина його дуг, відкидання якої унеможливлює маршрут від початкової до кінцевої вершини./

Приклад. Є транспортна мережа (рис. 7.3), якою потрібно перевозити продукцію з пункту 1 до пункту 8 через відповідні проміжні пункти.

 

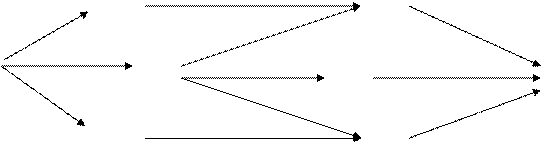
Рис. 7.3. Граф транспортної мережі

 

Усі проміжні пункти занумеровані числами від 2 до 7. Відомі пропускні спроможності щодо перевезення цієї продукції на кожній окремій ділянці мережі – з відповідного пункту 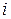безпосередньо до певного пункту 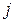– які наведено у таблиці 7.2 (зафарбована клітинка таблиці означає, що безпосереднє перевезення продукції між відповідними пунктами неможливе).