Виды моделей

Как отмечалось выше, для описания программы и осуществления компьютерного моделирования необходимо использовать формализованную модель объекта. Рассмотрим какие виды моделей существуют.

Все существующие модели можно разделить на две группы – физические модели и модели спецификации.

Физические модели являются реальными телами, которые своими физическими характеристиками выражают свойства исследуемого объекта.

Под моделями спецификациями понимают все остальные существующие модели, которые описывают физические характеристики моделируемого объекта с помощью принятых обозначений.

Среди физических моделей можно выделить следующие группы:

- в зависимости от учета фактора времени статические и динамические;

- по силе использования физической аналогии: натурные, масштабные и аналоговые;

- в зависимости от поставленных задач: демонстрационные, экспериментальные и т.д.

- в зависимости от количества используемых измерений: одно-, двух-, трехмерные.

Статические физические модели помогают нам наглядно представить себе пространственные соотношения. Их примером могут быть макеты заводских сооружений, или макеты сложной штамповочной оснастки.

Динамическая физическая модель должна учитывать время или развитие процесса во времени. Примером динамической физической модели может служить штамповочный участок, используемый для освоения нового технологического процесса, внедряемого на заводе.

Физические модели могут быть натурными – полномасштабными макетами (опытные образцы для штамповки), или масштабными – выполняемыми в уменьшенном или увеличенном масштабе, (например, модель кристаллической решетки, модель атома). Отличительной особенностью любой натурной и масштабной физической модели является то, что она “выглядит” подобно моделируемому объекту.

Аналоговыми моделями являются модели, у которых изучаемое свойство реального объекта заменяется аналогичным по поведению свойством другого объекта. Как правило, эта задача решается заменой свойств моделируемого объекта свойствами модели, после чего полученные результаты рассматриваются применительно к исходным свойствам моделируемого объекта.

Например, необходимо оценить качество заполнения опоки при литье детали, показанной на рисунок 2. Это можно сделать заменой формы опоки на электросопротивление проводников в цепи с током. Для этого форму опоки можно разбить на несколько участков, каждый из которых заменить проводником с определенным электросопротивлением. Причем для замены каждого участка электросопротивление подбирать относительно размеров и формы опоки на данном участке. В этом случае оценку качества заполнения опоки можно дать по течению в проводнике электрического тока.

 

а)   б)

 

 

Рисунок 2 – Пример аналоговой модели: а – опока; б – аналоговая модель опоки

 

Среди моделей спецификаций записываемых в письменном виде наиболее распространены математические модели – модели, представленные с помощью средств математики. Математические модели могут быть геометрическими, динамическими, логическими и т.д., в зависимости от того какие интересующие свойства они отражают.

Математические модели могут быть символическими, численными и смешанными, в зависимости от того используется обозначение величины или ее численное значение.

Математические модели можно разделить на две группы: функциональные и алгоритмические. Функциональные модели являться явно выраженными зависимостями между входными данными и исследуемыми свойствами, в то время как в алгоритмических моделях эта связь задана неявно, а в виде алгоритма. Можно сказать, что функциональные модели это частный случай алгоритмических, когда алгоритм вычисления сведен к расчету одного уравнения /3/.

При рассмотрении иерархических уровней математических моделей металлургического производства можно выделить несколько уровней: микроуровень, макроуровень, и метоуровень /27, 28/. Особенностью модели на микроуровне является отображение физических процессов в непрерывном пространстве и времени. С помощью дифференциальных уравнений в частных производных рассчитываются поля напряжений и деформаций. Объектами исследования на этом уровне являются отдельные технологические операции.

На макроуровне используют укрупненную дискретизацию производства по функциональному признаку, т.е. используют обыкновенные дифференциальные уравнения. В этих моделях обычно иметься две группы переменных – независимых (время) и зависимых (фазовых). В качестве фазовых переменных выступают силы, скорость перемещения, напряжения и т.д. В качестве объектов исследования выступают целые технологические процессы.

Объекты на метоуровне описывают укрупнено. В качестве математического аппарата используются обыкновенные дифференциальные уравнения, теория массового обслуживания, и т.д. Объектами выступают уже целые технологические системы.

Среди моделей спецификаций можно также выделить статические и динамические, детерминированные и стохастические, аналоговые и дискретные модели.

Статические модели описывают статические состояния, в них не присутствует время в качестве независимой переменной. Динамические модели отражают поведение системы во времени.

Стохастические и детерминированные модели различают в зависимости от учета или не учета случайных факторов. В детерминированных задачах вероятность совершения исследуемого события всегда равна 100% в то время как в стохастических задачах эта вероятность может изменяться или даже быть неизвестной /29/.

В аналоговых моделях переменные величины являться непрерывными, в дискретных – дискретными. Важным частным случаем дискретных моделей являются логические или булевы модели, в них состояние системы и ее элементов описывается булевыми величинами. В ряде случаев применяют смешанные по этому признаку модели. В них одна часть системы описывается аналоговыми моделями, другая - дискретными.

В дальнейшем мы будем говорить, только о функциональных математических детерминированных моделях спецификации, используемых для расчета на ЭВМ, называя их просто моделями или математическими моделями.

 

1.3 Формализация объектов и процессов при построении модели

Для того чтобы использовать ЭВМ в процессе моделирования необходимо, чтобы исходный объект или процесс был формализован, т.е. описан математическими зависимостями. Построение математической модели объекта или процесса называют её формализацией. В ходе формализации происходит описание исходного объекта с заданной точностью.

Следует заметить, что реальные процессы, как правило, включающие в себя огромное число переменных, параметров, факторов, элементов, соотношений, ограничений и т. д. Соответственно и при построении модели, в нее можно включить бесконечное число переменных параметров и т.д., что значительно усложнит процесс поиска верного варианта решения.

При создании модели следует пренебречь частью реальных факторов, переменных, параметров и т.п. изучаемого объекта и выделить только те особенности, которые необходимы для описания идеализированного варианта реального объекта или процесса. При оценке процессов и объектов ОМД можно воспользоваться правилом Паретто справедливым для большинства технических систем. Правило Паретто заключается в том, что на интересующие исследователя характеристики системы оказывает существенное влияние лишь несколько из множества факторов. Как правило, 20% факторов определяют 80% интересующих свойств, в то время как оставшиеся 80% факторов определяют оставшиеся 20% свойств /26/.

Таким образом, важной задачей моделирования является правильный выбор исследуемых факторов, поскольку именно правильное решение этой задачи позволяет значительно сэкономить силы и средства исследователей.

В большинстве случаев выбор исследуемых факторов осуществляется на основании уже накопленной информации, опыта и интуиции исследователя. Поэтому моделирование является творческим процессом, который может быть сравнен с искусством.

Любая модель является упрощением реального процесса. Если это упрощение выполнено правильно, то с помощью модели можно получить верные результаты.

Для того чтобы модель была “похожа” на объект необходимо, чтобы выполнялись следующие условия. Во-первых, должно существовать однозначное соответствие между элементами модели и элементами представляемого объекта. Во-вторых, должны быть сохранены точные соотношения или взаимодействия между элементами.

При разработке модели систему обычно разбивают на части, т.е. проводят анализ. Анализ необходим для выявления взаимодействия между элементами исследуемого объекта или процесса.

Например, в ходе анализа автоматизированного производственного участка листовой штамповки можно выделить отдельные взаимодействующие единицы оборудования (подающее и разматывающее устройство, штамповочный пресс и т.д.) и установить параметры взаимодействия между этими единицами (компенсационный запас материала, частоту включения разматывающего устройства и т.д.) /19/. При необходимости каждую единицу оборудования можно разбить на отдельные механизмы (на штамповочном прессе это может быть механизм подачи, механизм привода ползуна и т.д.), и установить параметры их взаимодействия (например, скорость подачи материала, величину его перемещения и т.д.).

 

При анализе очень часто приходиться сталкиваться с другого рода упрощениями исследуемого объекта. Данное упрощение, как правило, связано с заменой сложного характера зависимости реального объекта на более простой закон, используемый при построении модели. Например, при моделировании процессов ОМД зависимость между напряжениями и деформациями кривой упрочнения часто заменяют на более простой линейный закон аппроксимации (рисунок 5). В этом случае известно, что зависимость между напряжениями и деформациями является нелинейной, однако если принятое допущение о линейном характере зависимости на взгляд исследователя оправдано (например, если исследование проводиться на участке где линейная зависимость достаточно точно описывает кривую упрочнения см. рисунок 4), то мы можем принять данное допущение.

 

 

Рисунок 3 – Автоматизированный участок листовой штамповки:

1 – разматывающее устройство; 2 – валковая подача; 3 – ножницы для резки отходов; 4 – пресс

 

Еще одна сторона упрощения связана со сравнением порядка различных величин, фигурирующих в модели.

Например, изменение некоторой величины у с течением времени можно описать уравнением вида:

у=ах²+вх+с,

где у – исследуемая величина, х – переменная, определяющая исследуемую величину, а, в, с – параметры уравнения.

В случае если а<<в и а<<с, а значение х<1 то множителем ах² можно пренебречь и уравнение принимает более простой вид:

y=bx+c.

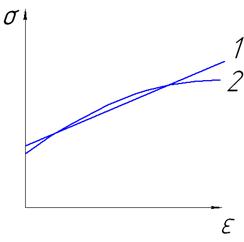
Рисунок 4 – Иллюстрация к замене кривой упрочнения линейным отрезком: 1 – степенная зависимость, 2 – линейная зависимость

 

После того как отдельные элементы системы были проанализированы и упрощены, очевидно, что необходимо осуществить задачу синтеза модели. Здесь надо учесть, что в ходе синтеза элементы должны быть собраны корректно, как с точки зрения характера взаимодействия, так и с точки зрения соединения объектов. Другими словами при передаче информации от одной части системы к другой передача должна осуществляться в одинаковом виде и в правильной последовательности. При этом не должно происходить потерь информации.

Например, на этапе анализа было выяснено, что кривую упрочнения можно разделить на два участка упругий и пластический и что каждый из участков можно заменить линейными зависимостями, с устраивающей исследователя точностью. Тогда на этапе синтеза необходимо объединить уравнения этих прямых в одну систему таким образом, чтобы полученная система полностью определяла исследуемую зависимость на исследуемом участке. Для этого необходимо найти точку пересечения этих прямых. Полученная в результате зависимость носит название билинейного закона.

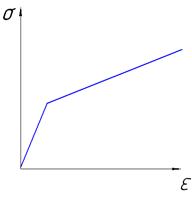а) б)

Рисунок 5 – Иллюстрация к задаче синтеза с кривой упрочнения 1: 2 – прямая, описывающая упругий участок, 3 – прямая, описывающая пластический участок

 

Следует заметить, что прямая описывающая пластические свойства может быть неограниченна справа по оси деформаций. Однако, с увеличением деформаций достоверность описания прямой пластического участка кривой упрочнения становиться ниже, поэтому необходимо ввести критерий, позволяющий судить о возможности использования принятой модели. Для оценки соответствия модели и исследуемого объекта или процесса, существует понятие адекватности (достоверности).

Существует несколько аспектов проверки адекватности. Во-первых, сама модель должна быть непротиворечивой и подчиняться законам логики. Во-вторых, достоверность модели во многом зависит от способности правильно описывать исходную ситуацию, т.е. от тех исходных допущений, которые были приняты при создании модели.

При получении достоверного решения нужно помнить о том, что уточнение решения для модели, должно быть оправдано, прежде всего, самой постановкой задачи. В первую очередь это касается точности имеющихся данных. Если исходные данные известны с погрешностью 10% (большинство задач ОМД), то смысла искать решение с точностью 1%, нет. В этом случае можно сказать – “всякое уравнение длиной более двух дюймов, скорее всего, неверно!” /26/.

При оценке достоверности необходимо помнить также и о затратах времени и ресурсов, связанных с получением более точного решения. Порой менее точное решение, полученное своевременно может дать больше выгоды.

Например, для получения быстрого решения при моделировании процесса вытяжки в программе AutoForm предусмотрен специальный модуль, который позволяет получить приближенное решение задачи и оценить с технологической точки зрения возможность изготовления изделия. На основании полученного решения у компании, использующей программу AutoForm, есть возможность быстро ответить потенциальному заказчику сможет ли она изготовить изделие и какова будет его примерная стоимость изготовления.

В заключение еще раз следует сказать то, что математическая модель представляет собой упрощение реальной ситуации. “Ощутимое упрощение наступает тогда, когда несущественные особенности ситуации отбрасываются и исходная сложная задача сводится к идеализированной задаче, поддающейся математическому анализу” /1/.

 

1.4 Требования, предъявляемые к моделям

Моделирование всегда связано с решением конкретных задач, которые не должны давать абсурдные результаты. Желательно, чтобы была возможность изменения величины параметров и переменных в как можно большем интервале измерений, поскольку это позволяет изучить модель на всю глубину исследуемых параметров. Желательно также, чтобы модель могла ответить на вопрос – “а что, если...?”, поскольку именно этот вопрос позволяет ее изучить наиболее полно.

Необходимо также помнить о том для кого предназначается информация, которая появляется при моделировании. Нет смысла разрабатывать модель, если ей в конечном итоге невозможно воспользоваться.

При построении модели надо также учитывать и тот факт что со временем ситуация может измениться и разрабатываемая модель должна иметь возможность адаптироваться (подстроиться) к новым условиям. Изменения могут быть связаны как с изменением интервала значений уже рассматриваемых параметров, так и с появлением новых значимых параметров. Следовательно, и модель должна иметь возможность к подобной адаптации.

Модель должна быть экономичной. Экономичность модели определяется, как затратами, затрачиваемым пользователем модели на ее использование, так и возможностью быстрого перестроения модели исследователем.

Основываясь на вышеизложенном, можно сформулировать основные требования предъявляемые к модели. Модель должна быть:

· точной – обеспечивающей совпадение результатов эксперимента, полученных от реального объекта, с данными, полученными от модели;

· экономичной;

· целенаправленной – не содержащей лишней, ненужной информации;

· полной с точки зрения возможностей решения главных задач;

· адаптивной, позволяющей легко переходить к другим модификациям или обновлять данные,

· простой и понятной для использующего модель пользователя.

Для того чтобы моделью можно было пользоваться, при ее разработке должны быть тщательно продуманы и потребности, и психология ее конечного потребителя.

 

1.5 Общий вид математических моделей

 

1.5.1 Общий вид математических моделей

Математическая модель, это модель, которая в общем случае представляет собой записанный с помощью средств математики алгоритм вычисления вектора выходных параметров Y при заданных входных параметрах X.

Математические модели являются представлением физических или иных процессов, протекающих в объектах. Обычно данные модели представляют систему уравнений, описывающих внутренние, внешние и выходные параметры (см. далее).

В самом простом случае структуру аналитической модели мы можем представить математически в виде следующей системы:

,

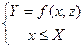где Y=f(x,z) – целевая функция, х≤Х – возможные ограничения, Y – результат действия системы; х, z – переменные и параметры; f – функциональная зависимость между параметрами и переменными определяющая величину Y. Данная система содержит одну целевую функцию и одно ограничение. В общем случае математическая модель может содержать несколько целевых функций и несколько ограничений.

Тогда любая математическая модель может содержать следующие составляющие /21/:

— компоненты,

— переменные,

— параметры,

— функциональные зависимости,

— ограничения,

— целевые функции.

Под компонентами понимают составные части, образующие систему. В качестве компонентов могут выступать ограничения и целевые функции. Иногда под компонентами понимаются элементы системы или ее подсистемы. Например, если в качестве системы рассматривать технологический процесс, то компонентами этой системы будут отдельные операции. Полное количество компонентов участвующих в моделировании выбирается исследователем.

Параметры это величины, выбирающиеся произвольно в отличие от переменных, которые принимают только значения, определяемые видом используемой функции, т.е. параметры являются постоянными величинами, не подлежащими изменению. Например, в законе Гука (1): Е является параметром постоянной величиной для заданного материала, а σ и ε — переменными.

σ=Еε, (1)

где σ – напряжения, Е – модуль Юнга, ε – деформации.

Переменные могут быть двух видов - внутренними и внешними. Внешние переменные называют также входными, поскольку они являются результатом воздействия внешних причин. Переменные, возникающие в системе, называются внутренними. Они появляются в результате воздействия внутренних причин. Внутренние переменные могут быть переменными состояния, если они характеризуют состояние или условия, имеющие место в системе или выходными переменными, если они описывают состояние на выходах системы /21/.

Функциональные зависимости характеризуют переменные и параметры в пределах компонента или выражают соотношения между компонентами системы. Эти соотношения, могут быть различными по своей природе и используемому математическому аппарату. По природе исследуемого объекта соотношения могут быть детерминистскими, или стохастическими. Детерминистские соотношения – это уравнения устанавливающие зависимость между переменными или параметрами в случае, когда процесс однозначно определен. Стохастические соотношения однозначно не определяются с помощью входных параметров.

Функциональные зависимости могут быть получены в соответствии с двумя подходами: гносеологическим или информационным (см. далее). Как правило, стохастические соотношения между входными и выходными переменными характерны для информационного подхода.

Ограничения являются математической записью пределов изменения значений переменных. Они могут быть поставлены разработчиком – искусственные ограничения, или природой исследуемых объектов в соответствии с присущими им свойствами – естественные ограничения. Как правило, искусственные ограничения являются техническими требованиями к объекту или процессу. Например, требование предъявляемое к поковке по штамповочному уклону служит ограничением при моделировании процесса заполняемости штампа при штамповке.

Примером естественного ограничения может быть максимальное и минимальное значение процентов содержания компонента сплава, которое может изменяться от 0 до 100%. В качестве примера искусственного ограничения можно привести ограничения связанные с поиском сплава с наибольшей прочностью при изменении процентного содержания одного из компонентов в диапазоне от 10 до 25%.

Целевая функция, или функция критерия, - является отражением целей или задач моделирования. Уравнение целевой функции должно быть, как можно более точно определено относительно целей задач исследования. Под критерием понимается конкретная мера оценки позволяющая давать верное суждение о суть происходящих явлений. Такое определение критерия объясняется двумя причинами. Во-первых, выбор критерия влияет на процесс создания модели и работу с ней. Во-вторых, неправильное определение критерия обычно ведет к неправильным заключениям. Функция критерия (целевая функция) является основой модели. Практически процесс исследования модели и решения задачи оптимизации полностью связан с исследованием целевой функции.

В зависимости от сложности поставленной задачи математическая модель может содержать несколько целевых функций, в этом случае говорят, что задача моделирования является многокритериальной.

 

1.5.2 Основные этапы формализации объектов и процессов при построении математической модели

 

Процесс создания математической модели, которая в дальнейшем может использоваться для создания программы, содержит следующие этапы:

1. постановка задачи,

2. анализ и упрощение данных,

3. синтез структуры модели,

4. проверка адекватности модели,

5. принятие решения о доработке модели или ее использовании.

На первом этапе необходимо определить, в чем именно заключается задача формализации, и какие результаты необходимо получить за счет изменения параметров.

На втором этапе исследователю необходимо на основании анализа элементов упростить реальный объект или процесс и поставить ограничения. Процесс упрощения достаточно подробно изложен в пункте (1.3) формализация объектов и процессов при моделировании. Как правило, при постановке ограничений для установления области исследования пользуются здравым смыслом (например, при моделировании свойств нового сплава состоящего из большого количества компонентов содержание любого из компонентов не может быть более 100%). В другом случае ограничения могут быть сформулированы при постановке задачи (например, постановка задачи звучит следующим образом: уточнить концентрацию компонента в сложном сплаве в интервале от 10 до 15% так чтобы прочность сплава была наибольшей).

На третьем этапе, на основании уже формализованных данных создается сама модель. Этот этап можно разделить на две части. Во-первых, записывается сама модель (система уравнений) без конкретизации числовых значений используемых параметров. Во-вторых, осуществляется расчет и уточнение числовых значений ранее записанной модели.

На четвертом этапе осуществляется проверка адекватности построенной модели. На этом этапе желательно осуществить постановку эксперимента с целью подтверждения созданной модели.

На пятом этапе, на основании теоретической или экспериментальной проверки принимается решение о доработке модели или ее использовании. В случае, если для моделирования использовалось несколько различных вариантов моделей, производиться выбор наиболее подходящего варианта.

 

1.5.3 Основные подходы в математическом моделировании

Для построения математических моделей можно использовать два подхода: гносеологический (аналитический) и кибернетический (информационный) /2/.

Аналитический подход позволяет получить математическое описание процесса на основе теоретического анализа физических процессов, происходящих в исследуемом объекте с учетом особенностей и характеристик обрабатываемого материала. Постановка эксперимента при использовании данного подхода осуществляется только для уточнения и проверки уже построенной модели /2/.

Построенные на основании данного подхода модели являются наиболее полными и используются для анализа явлений, протекающих в объекте. После аппроксимации простыми зависимостями эти модели можно использовать в задачах оптимизации и автоматического управления.

Кибернетический подход – базируется, на изучении входных и выходных переменных кибернетической системы, которую называют “черным ящиком” (рисунок 6). “Черный ящик” представляет собой систему связей, недоступную для наблюдения, т.е. неизвестен характер связи входов Х и выходов Y участвующих в процессе /4, 5, 6, 7, 26/.

Данный подход дает математические модели, которые описывают поведение объекта, а не его физическую сущность. Модели, построенные на основании данного подхода так же, используются для оптимизации и автоматического управления.

Рассмотрим пример использования гносеологического и кибернетического подходов. Допустим, что необходимо исследовать какое влияние на толщину фланца заготовки в ходе процесса вытяжки оказывает величина исходного диаметра заготовки. Напомним, что процесс вытяжки заключается в получении цилиндрической оболочки с дном из плоской заготовки рисунок 7.

В соответствии с кибернетическим подходом необходимо провести серию экспериментов для получения исходных данных. Полученные из экспериментов данные математически обработать и выяснить, есть ли между исходным диаметром заготовки и толщиной фланца зависимость или нет. В случае, если зависимость наблюдается, необходимо провести дополнительное исследование полученной модели с тем, чтобы установит аналитическую зависимость влияния диаметра заготовки на толщину фланца. Аналитические зависимости строят в виде уравнения регрессии с заданной степенью надёжности и проверкой адекватности.

 

 

Рисунок 6 – Схема “черного ящика”: Х – информация, поступающая на вход;

Y – информация, поступающая на выход

 

В соответствии с аналитическим подходом необходимо провести теоретическое исследование процесса вытяжки. Для этого обратимся к теории листовой штамповки.

 

 

Рисунок 7 – Вытяжка цилиндрической детали из круглой плоской заготовки:

1 – матрица; 2 – заготовка; 3 – пуансон; 4 - прижим

 

Согласно теории листовой штамповки надо воспользоваться уравнением связи напряжений и деформаций и условием постоянства объема, которые для листовой штамповки могут быть записаны в следующем виде /8,9/:

,

,

где 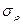,- меридиональное и широтное напряжения; , 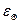- деформации в соответствующих направлениях, 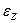- деформация по толщине.

Откуда:

.

После преобразований получим:

.

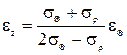Считаем, что , а можно записать:

,

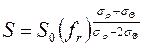где S, S₀ – соответственно толщины до и после деформации рассматриваемого элемента с координатой , r – радиус рассматриваемого элемента до деформации. Поскольку при , то для кромки деформируемой заготовки можно записать:

,

где , - радиусы заготовки и кромки в рассматриваемый момент деформации. Основываясь на этом соотношении, можно примерно оценить толщину фланца заготовки при вытяжке. В случае использования данного подхода моделирования решение было получено “на бумаге” и практически все затраты сводятся лишь к затратам времени на теоретическое исследование.

В данной работе в дальнейшем будет рассматриваться только гносеологический подход моделирования.

1.5.4 Основные допущения, используемые при создании математических моделей процессов ОМД

Использование гносеологического подхода позволяет получать математическое описание объекта, основываясь на анализе физических, химических и др. явлений, протекающих в исследуемом объекте.

Существенным недостатком аналитических моделей, как правило, является сложный характер взаимосвязи, участвующих при построении модели параметров, что создает неудобства при дальнейшем использовании полученной модели, например, в поиске оптимального значения исследуемых параметров, или в автоматическом управлении технологическим процессом.

Сложный характер явлений, возникающих при обработке металлов, требует упрощения сложных математических моделей.

Это возможно за счет аппроксимации (замены) аналитически полученной зависимости более простыми и удобными для использования зависимостями, которые и могут быть использованы для дальнейшего управления технологическим процессом или поиска оптимального значения. В этом случае точность используемой модели будет ниже, но сама модель будет более удобной для исследования или управления технологическим процессом.

В соответствии с данным подходом появляется возможность получать модели требуемой точности зависимой лишь от степени достоверности.

Задачи ОМД, решаемые наиболее часто с помощью моделирования можно разделить на 2 группы:

· Задачи теплообмена. Решая эти задачи, осуществляется подбор различных режимов ОМД для различных по форме деталей из различных материалов, учитывать влияние термических напряжений на форму и свойства детали после предлагаемой обработки.

· Задачи описания процессов, протекающих в металле при его деформации. Они позволяют осуществлять расчет технологических параметров процессов ОМД, оценить качество возможного изделия, и оценить стойкость оснастки.

Рассмотрим первую группу задач. Как правило, задачи этой группы являются наиболее простыми с точки зрения моделирования, поскольку рассчитывают перенос тепла в твердом теле теплопроводностью /10/. Напомним, что в общем случае перенос тепла может осуществляться тремя способами: теплопроводностью, конвективным теплообменом и лучистым теплообменом.

В случае теплопроводности перенос тепла осуществляется между твердыми соприкасающимися частицами. Поэтому используемая в моделировании теория теплопроводности рассматривает исследуемое тело, как непрерывную среду – континуум. В этом случае не учитывается реальное молекулярное или атомное взаимодействие частиц реального тела. На самом деле как процессы, протекающие внутри тела, так и процессы, связанные с взаимодействием тел объясняются именно взаимодействием частиц на атомном и молекулярном уровнях /11/.

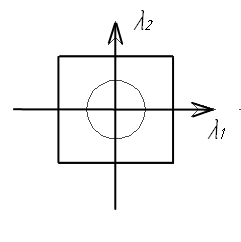
Другое допущение связано с тем, что при моделировании задач теплопроводности могут использоваться изотропные и ортотропные модели. В изотропной модели свойства теплопроводности одинаковы во всех направлениях по всему телу, в то время как в ортотропной модели свойства различны в зависимости от направления (рис. 8) /12/. Если выделить в теле элемент сплошной среды и считать, что оси координат совпадают с главными направлениями теплопроводности, то количество теплоты, проходящее через изотермическую площадку в единицу времени определяется величиной коэффициента теплопроводности в указанном направлении (рисунок 9) /11/.

Задачи теплообмена, решаемые совместно с задачами пластического деформирования металла реализуются, например, в программе Deform.

Рассмотрим вторую группу задач. Задачи механики твердого тела являются наиболее сложными задачами инженерного анализа.

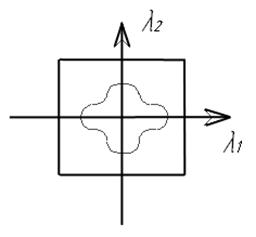а) б)

 

Рисунок 8 – Иллюстрация к свойствам теплопроводности: а – изотропное тело; б – ортотропное тело.

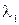- коэффициент теплопроводности в направлении 1,

- коэффициент теплопроводности в направлении 2

 

В данной группе задач помимо допущения о сплошности тела и однородности его свойств используется также допущение (гипотеза) о несжимаемости тела. Согласно данному допущению осуществляется пренебрежение упругим сжатием тела изменение его объёма за счёт существующих дефектов структуры. Наиболее распространена запись этой гипотезы в виде условия постоянства объема, по которому изменение объёма тела в трех взаимно перпендикулярных направлениях равна нулю.

 

 

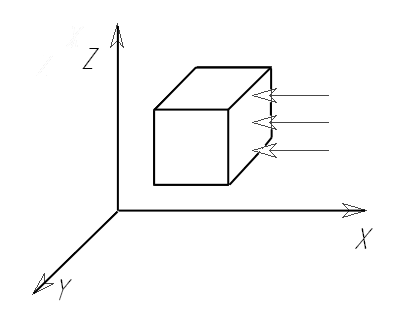
Рисунок 9 – Иллюстрация к описанию задачи теплопроводности

 

Из курса теории обработки металлов давлением известно, что детали меняют форму под действием внешних сил. Действие внешних сил вызывает в теле внутренние усилия, значение и распределение которых зависит от геометрии тела и характера приложения нагрузки.

Рассмотрим тело, находящееся под действием внешних сил. Внешние силы вызывают в теле реактивные силы, которые противодействуют внешним силам. Если мысленно выделить внутри такого тела бесконечно малый элемент в виде прямоугольного параллелепипеда, то действие внутренних сил сопротивления на его гранях эквивалентно действию сил со стороны отброшенных внешних частей (рисунок 10) и противоположны по знаку.

Здесь допущение принять на философском, мировоззренческом уровне. За бесконечно малый элемент принят самый малый объём, который сохраняет механические свойства основного металла. Другими словами остаётся вне рассмотрения свойства на атомном уровне.

В соответствии с теорией механики сплошных сред напряженное состояние тела в точке характеризуется с помощью тензора напряжений. Под тензором напряжений понимается совокупность в общем случае девяти напряжений, действующих на бесконечно малых площадках вокруг рассматриваемой элемента (рисунок 10).

Если рассматривать элементарный прямоугольный параллелепипед, находящийся в равновесии под действием внутренних сил, то его длина по отношению к исходному состоянию, когда усилие не было приложено, изменится. Это явление называется деформированием, а мера изменения размера – деформацией. Аналогично тензору напряжений деформированное состояние тела принято описывать с помощью тензора деформаций (рисунок 11). Здесь деформации сдвига, имеющие в индексах одинаковые буквы, равны между собой, поэтому неизвестными являются только шесть компонентов деформаций.

 

 

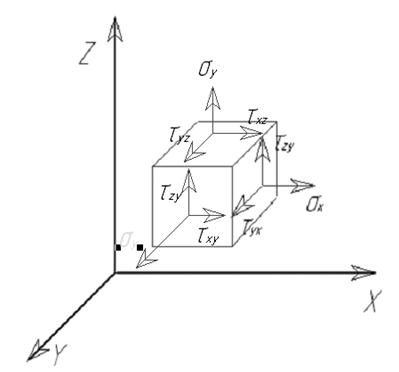
Рисунок 10 – Напряженное состояние бесконечно малого элемента.

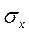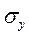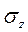, , - главные напряжения, , , 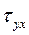, ,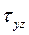, 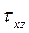- касательные напряжения

 

Рисунок 11. Деформированное состояние бесконечно малого элемента:

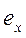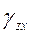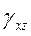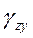, , -главные деформации, , ,,,,-сдвиговые деформации

 

1.5.5 Методы решения задач ОМД

Для определения напряженно - деформированного состояния тела достаточно иметь три уравнения равновесия:

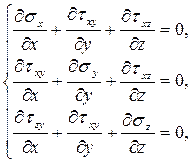
шесть кинематических уравнений связи деформации с перемещениями:

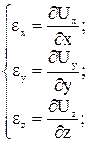
где - перемещение в направлении i-ой оси,

шесть физических уравнений:

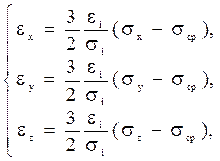
где ,

уравнения интенсивности деформации:

,

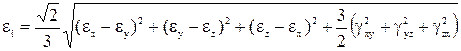уравнение, описывающее физические свойства материала:

,

где А и n – константы, описывающие механические свойства материала.

 

 

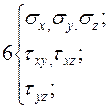
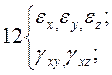
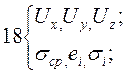
Эта система уравнений является моделью описывающей напряженно деформированное состояние любого тела подвергающегося внешней нагрузке, содержит восемнадцать уравнений с восемнадцатью неизвестными, т.е. статически определима. Однако математически решить данную систему для конкретного процесса в большинстве случаев невозможно. Поэтому в ОМД приходиться использовать специальные и упрощенные методы решения систем уравнений. К ним относят:

метод решения упрощенных уравнений равновесия и пластичности;

метод сопротивления материалов пластическим деформациям;

метод характеристик.

Суть всех методов одна, и заключается в том, что производиться упрощение существующих физических законов, описываемых сложными дифференциальными уравнениями до более простых дифференциальных зависимостей, которые позволяют найти приближенное решение исходной системы /13/.

В ряде случаев задача интегрирования исходной системы дифференциальных уравнений может быть заменена на задачу поиска некоторого значения энергетического функционала. Методы, использующие данный математический подход, называются вариационными /13/.

Наиболее широко используемый в настоящее время в программных продуктах метод конечных элементов (МКЭ) то же является вариационным. Данный метод является одним из вариантов решения метода Ритца, который путем минимизации потенциальной энергии тела сводит задачу к системе линейных уравнений. Данный метод нашел применение не только для решения задачи механики сплошных сред, но и для описания многих других физических процессов.

Суть МКЭ заключается в том, что непрерывные величины можно заменить на модель, состоящую из отдельных участков (элементов). При этом на каждом из участков исследуемая непрерывная величина заменяется кусочно-линейной непрерывной функцией, построенной на значениях непрерывной исследуемой величины в конечном числе точек.

Распределение значений исследуемой величины внутри области и сама непрерывная величина, могут быть неизвестны. При построении дискретной модели мы предполагаем, что численные значения исследуемой величины в конкретных точках (узлах) на границах нам известны. После этого можно перейти к определению значений кусочно-непрерывной функции, за счет подбора значений в узловых точках так, чтобы выполнялось условие минимизации потенциальной энергии.

Таким образом, осуществляется следующая последовательность действий:

1. Область определения исследуемой величины разбивают на КЭ. Эти элементы связаны друг с другом с помощью узлов. Элементы в совокупности аппроксимируют (описывают) форму исследуемого тела.

2. Значение исследуемой непрерывной величины в каждом узле предстоит определить в зависимости от поставленных граничных условий.

3. Подбирая значения непрерывной исследуемой величины в узловых точках, определяют ее значения внутри рассматриваемой области (тела).

Аппроксимирующие функции подбираются таким образом, чтобы сохранить непрерывность исследуемой величины вдоль границ элемента. В виде аппроксимирующей функции могут выступать линейные, квадратичные и кубические полиномы, которые для данного элемента называются функцией элемента.

Рассмотрим в качестве примера расчет с помощью МКЭ осевого растяжения ступенчатого стержня /14/. Ступенчатый стержень жестко заделан с левого края и имеет сечения А₁ и А₂, нагружен с правого торца растягивающим усилием Р. Требуется определить перемещение сечений 1, 2, 3 (рисунок 11).

 

 

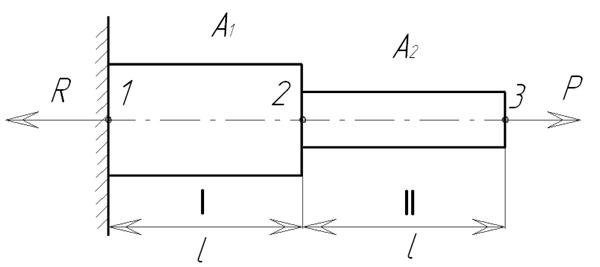
Рисунок 11 – Ступенчатый стержень

 

Разобьем стержень на два элемента (I, II) так, чтобы граница между элементами проходила в месте изменения перпендикулярного к длине сечения стержня. Введем на границах элементов узлы 1, 2, 3, в которых будем искать перемещения u. В результате такого упрощения мы будем решать задачу растяжения двух стержневых элементов, каждый из которых имеет длину l₁ и l₂, площадь (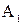и ) приложенное к узлам усилие (Р₁и Р₂) и смещения (u_1,u₂), которые появляются от действия этого усилия (рисунок 12).

Для любого из этих элементов согласно теории сопротивления материалов можно записать значения усилия действующего в узлах:

P₁ = 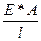(u₁ – u₂);

P₂ = 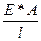(u₂ – u₁),

где Е модуль упругости.

 

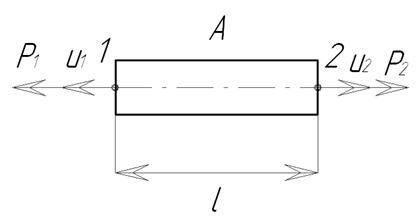
Рисунок 12 – Элемент стержня.

 

Для каждого элемента систему узловых усилий можно записать следующим образом:

=

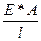
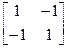
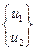
или

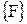= (1)

Рассмотрим последнее уравнение более подробно. В нем 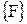называется матричным вектором усилий, – вектором перемещений или степеней свободы, 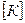– матрицей жесткости.

Вернемся к ступенчатому стержню. Очевидно, что поскольку стержень состоит из нескольких элементов, то для решения задачи необходимо объединить соотношения для элементов 1 и 2 с учётом их положения в пространстве (или взаимодействия по узлам). Тогда можно записать 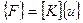или

= ,

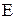
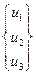где в векторе усилий 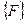уже учтено то, что R является реакцией опоры приложенной в узле 1, а Р является растягивающим усилием, приложенным в узле 3, а узел 2 свободен от нагрузок.

У нас осталось неиспользованное ограничение по перемещению (u₁=0). Его можно использовать для упрощения решения системы, если заменить в матрице жесткости первую строку и первый столбец на нули а элемент матрицы, стоящий на главной диагонали заменить на единицу. Тогда уравнение примет вид:

_. = .

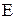
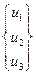Решением этого уравнения являются следующие значения перемещений.

u₁=0, u₂=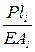_; u₃=.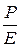

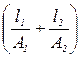Пространственное положение каждого из элементов приведённой выше системы описывается с помощью числа степеней свободы или вектором узловых перемещений. Обычно каждой степени свободы (узловому перемещению) соответствует сопрягаемые переменные усилия. Для расчета эти переменные усилия собираются в матричной вектор 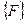. Произведение вектора сил 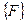на вектор степеней свободы является внешний энергией или работой совершаемой над телом внешними силами.

В приведенном примере одноосного растяжения стержня решение системы уравнений может быть получено просто и в явном виде. В случае моделирования более сложных тел приходится, задаваясь значениями перемещений, искать решение так, чтобы выполнялось условие минимизации энергии. В ходе такого решения значениями перемещений приходиться задаваться неоднократно, поэтому МКЭ носит название вариационного метода.

Рассмотренный нами пример позволяет определить напряжено- деформированное состояние тела на основании варьирования перемещений. В действительности термин МКЭ определяет более широкий набор математических способов расчета, среди которых в зависимости от того, какой величиной варьируют можно выделить следующие способы расчета:

· в перемещениях (минимум потенциальной энергии Лагранжа) – варьируются перемещения;

· в напряжениях (минимум дополнительной работы Кастильо) – варьируются напряжения;

· смешанные (принцип Райснера) – варьируются перемещения и напряжения;

· гибридные (принцип Ху-Вашицу) – варьируются перемещения, напряжения и деформации.

Наиболее часто используется принцип Лагранжа.

В зависимости от области науки, в которой используются МКЭ, смысл векторов 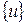и 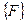может измениться (таблица 1).

Таблица 1 – Физический смысл векторов 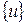и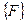

Область приложения	Вектор состояния	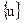Вектор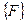
Механика твердых тел	Перемещение	Механическое усилие
Теплопроводность	Теплопроводность	Тепловой поток
Потенциальное течение	Давление	Скорость частицы
Общий вид течения	Скорость	Поток
Электростатика	Электрический потенциал	Плотность заряда
Магнитостатика	Магнитный потенциал	Интенсивность магнитного поля