рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Сложение коллинеарных скользящих векторов
Реферат Курсовая Конспект
Сложение коллинеарных скользящих векторов
Сложение коллинеарных скользящих векторов - раздел Философия, Ортогональный базис Если Скользящие Векторы Параллельны, То При Их Сложении Главная Трудность Сос...
Если скользящие векторы параллельны, то при их сложении главная трудность состоит в определении прямой, на которой будет расположена их сумма. (Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В механике при изучении статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные векторы. Пусть, например, надо сложить скользящие векторы  и
и 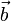 , расположенные на параллельных прямых. Добавим к ним векторы
, расположенные на параллельных прямых. Добавим к ним векторы 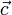 и
и  , расположенные на одной прямой. Прямые, на которых расположены векторы
, расположенные на одной прямой. Прямые, на которых расположены векторы  и
и 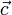 ,
, 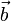 и
и  пересекаются. Поэтому определены векторы
пересекаются. Поэтому определены векторы
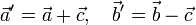
Прямые, на которых расположены векторы 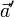 и
и  , пересекаются всегда, за исключением случая, когда векторы
, пересекаются всегда, за исключением случая, когда векторы  и
и 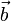 равны по величине и противоположны по направлению, в котором говорят, что векторы
равны по величине и противоположны по направлению, в котором говорят, что векторы  и
и 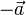 образуют пару (векторов).
образуют пару (векторов).
Таким образом, под суммой векторов  и
и 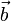 можно понимать сумму векторов
можно понимать сумму векторов 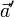 и
и  , и эта сумма векторов определена корректно во всех случаях, когда векторы
, и эта сумма векторов определена корректно во всех случаях, когда векторы  и
и 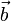 не образуют пару.
не образуют пару.
Вычитание[править | править исходный текст]
Операция вычитания из вектора  вектора
вектора 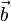 сводится к сложению первого вектора и вектора, противоположного второму:
сводится к сложению первого вектора и вектора, противоположного второму:

(Само сложение при этом осуществляется так, как описано в параграфе выше, пользуясь, если это удобно, любым из приведенных там альтернативных способов).
Однако легко видеть, что из правила треугольника можно получить и отдельное геометрическое определение разности. Для этого достаточно посмотреть на чертеж, иллюстрирующий сложение по правилу треугольника и осознать, что разность векторов 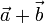 и
и  на этом чертеже есть вектор
на этом чертеже есть вектор  Отсюда прямо формулируется правило треугольника для вычитания векторов:
Отсюда прямо формулируется правило треугольника для вычитания векторов:
разность двух векторов с общим началом (или перенесенных параллельно так, чтобы начала совпали) есть вектор с началом, совпадающим с концом вычитаемого и концом, совпадающим с концом уменьшаемого.
Это правило также может быть удобным.
Скалярное произведение[править | править исходный текст]
Основная статья: Скалярное произведение


Скалярное произведение двух векторов
Скалярное произведение на множестве геометрических векторов вводится, как
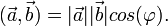
Скалярное произведение любого вектора  и какого-то единичного вектора
и какого-то единичного вектора  естьпроекция (ортогональная проекция) вектора
естьпроекция (ортогональная проекция) вектора  на направление этого единичного вектора:
на направление этого единичного вектора:
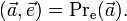
Легко видеть, что скалярное произведение может быть записано через операцию (ортогонального) проецирования:

(где 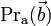 — проекция вектора
— проекция вектора 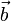 на направление
на направление  ,
, 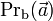 — проекция вектора
— проекция вектора  на направление
на направление 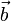 ).
).
- В абстрактном подходе обычно сперва вводят скалярное произведение, а уже через него определяют понятие угла, ортогональность, ортогональную проекцию.
Векторное произведение[править | править исходный текст]
Основная статья: Векторное произведение


Векторное произведение двух векторов
Векторным произведением вектора  на вектор
на вектор 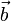 называется вектор
называется вектор 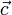 , удовлетворяющий следующим требованиям:
, удовлетворяющий следующим требованиям:
- длина вектора
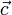 равна произведению длин векторов
равна произведению длин векторов  и
и 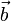 на синус угла φ между ними
на синус угла φ между ними
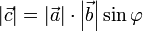
- вектор
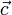 ортогонален каждому из векторов
ортогонален каждому из векторов  и
и 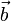
- вектор
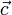 направлен так, что тройка векторов
направлен так, что тройка векторов 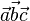 является правой.
является правой.
Обозначение: 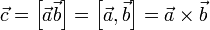
Геометрически векторное произведение 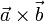 есть ориентированная площадьпараллелограмма, построенного на векторах
есть ориентированная площадьпараллелограмма, построенного на векторах 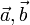 , представленная псевдовектором, ортогональным этому параллелограмму.
, представленная псевдовектором, ортогональным этому параллелограмму.
Свойства векторного произведения:
- При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е
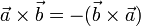
- Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть
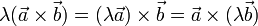
- Векторное произведение обладает распределительным свойством:
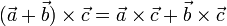


Геометрическая интерпретация смешанного произведения.
Смешанное произведение[править | править исходный текст]
Основная статья: Смешанное произведение
Сме́шанное произведе́ние 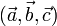 векторов
векторов 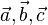 — скалярное произведениевектора
— скалярное произведениевектора  на векторное произведение векторов
на векторное произведение векторов 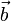 и
и 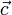 :
:
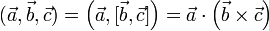
(равенство здесь записано для разных обозначений скалярного и векторного произведения, часто встречающихся в литературе).
Иногда смешанное произведение называют тройным скалярным произведениемвекторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрически смешанное произведение 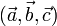 есть (ориентированный) объём параллелепипеда, построенного на векторах
есть (ориентированный) объём параллелепипеда, построенного на векторах 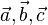 .
.
То есть абсолютная величина его есть просто объём этого параллелепипеда (в общем случае — косоугольного), а знак определяется тем, представляют ли векторы 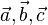 правую тройку (тогда плюс) или левую (тогда минус). Иногда при использовании левого базиса знак может быть определен противоположным образом.
правую тройку (тогда плюс) или левую (тогда минус). Иногда при использовании левого базиса знак может быть определен противоположным образом.
Базис и разложение по базису[править | править исходный текст]
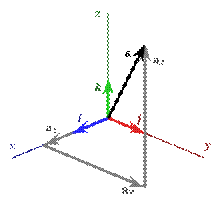

Разложение вектора по трём ортогональным векторам трёхмерного евклидова пространства
Векторы (как направленные отрезки), лежащие на прямых, параллельных одной прямой, называются коллинеарными, а векторы, лежащие в плоскостях, параллельных одной плоскости — компланарными. Для свободных векторов коллинеарность и компланарность определяется как такие понятия для изображающих их направленных отрезков (то есть представителей соответствующих свободным векторам классов эквивалентности).
Каждый вектор плоскости можно единственным образом разложить по двум определённым неколлинеарным векторам этой плоскости, а каждый вектор трёхмерного евклидова пространства можно единственным образом разложить по трём определённым некомпланарным векторам. Эти векторы, взятые в определённом порядке называются базисом плоскости (пространства). Сопоставлением каждому вектору данной плоскости (пространства) его коэффициентов в таком его разложении, определяется аффинная система координат на плоскости (в пространстве). Если векторы, по которым производится разложение, ортогональны и единичны, то получаемпрямоугольную декартову систему координат на плоскости (в пространстве). Разложение геометрического вектора по базису есть упорядоченная совокупность проекций вектора на базисные вектора.
Обозначения[править | править исходный текст]
Вектор, представленный набором  элементов (компонент)
элементов (компонент) 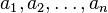 допустимо обозначить следующим способами:
допустимо обозначить следующим способами:
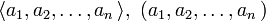 .
.
Для того, чтобы подчеркнуть, что это вектор (а не скаляр), используют черту сверху, стрелочку сверху, жирный или готический шрифт:
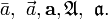
Сложение векторов почти всегда обозначается знаком плюс:
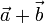 .
.
Умножение на число — просто написанием рядом, без специального знака, например:
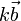 ,
,
причём число при этом обычно пишут слева.
Умножение на матрицу также обозначают написанием рядом, без специального знака, но здесь перестановка сомножителей в общем случае влияет на результат. Действие линейного оператора на вектор также обозначается написанием оператора слева, без специального знака.
Физическая интерпретация[править | править исходный текст]
В физике вектор является линией, показывающей направление какой-либо векторной величины
Вектор как последовательность[править | править исходный текст]
Вектор — (последовательность, кортеж) однородных элементов. Это наиболее общее определение в том смысле, что может быть не задано обычных векторных операций вообще, их может быть меньше, или они могут не удовлетворять обычнымаксиомам линейного пространства. Именно в таком виде вектор понимается в программировании, где, как правило, обозначается именем-идентификатором с квадратными скобками (например, object[]). Перечень свойств моделирует принятое втеории систем определение класса и состояния объекта. Так типы элементов вектора определяют класс объекта, а значения элементов — его состояние. Впрочем, вероятно, это употребление термина уже выходит за рамки обычно принятого в алгебре, да и в математике вообще.
С другой стороны, многие математические объекты (например матрицы, тензоры, функции и т. д.), в том числе обладающие структурой более общей, чем конечный (а иногда даже и чем счётный) упорядоченный список, удовлетворяют аксиомамвекторного пространства, то есть являются с точки зрения алгебры векторами.
История[править | править исходный текст]
Интуитивно вектор понимается как объект, имеющий величину, направление и (необязательно) точку приложения. Зачатки векторного исчисления появились вместе с геометрической моделью комплексных чисел (Гаусс, 1831). Развитые операции с векторами опубликовал Гамильтон как часть своего кватернионного исчисления (вектор образовывали мнимые компоненты кватерниона). Гамильтон предложил сам термин вектор (лат. vector, несущий) и описал некоторые операции векторного анализа. Этот формализм использовал Максвелл в своих трудах по электромагнетизму, тем самым обратив внимание учёных на новое исчисление. Вскоре вышли «Элементы векторного анализа» Гиббса (1880-е годы), а затем Хевисайд (1903) придал векторному анализу современный вид.
_____________________________________________________________________________________
– Конец работы –
Эта тема принадлежит разделу:
Ортогональный базис
Материал из Википедии свободной энциклопедии... Ортогональный ортонормированный базис ортогональная ортонормированная... Содержание Конечномерный случай Бесконечномерный случай Примеры Литература См также...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Сложение коллинеарных скользящих векторов
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов