Системы координат. Координатные базисы
Рассмотрим множество любых трех вещественных упорядоченных чисел  или
или 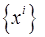 ,
, 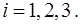 Если между множеством
Если между множеством 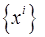 и точками пространства установлено взаимнооднозначное и непрерывное соответствие, то говорят, что пространство снабжено координатами или системой координат. Очевидно, что множеству чисел
и точками пространства установлено взаимнооднозначное и непрерывное соответствие, то говорят, что пространство снабжено координатами или системой координат. Очевидно, что множеству чисел 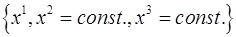 в этом случае соответствует в пространстве линейное множество точек, образующих линию, вдоль которой меняется значение только одной координаты
в этом случае соответствует в пространстве линейное множество точек, образующих линию, вдоль которой меняется значение только одной координаты 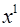 при постоянных значениях
при постоянных значениях 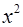 и
и 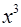 . Поэтому множеству
. Поэтому множеству 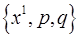 , где
, где 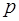 и
и  - произвольные постоянные, соответствует двухпараметрическое семейство кривых такое, что через каждую точку пространства (по крайней мере, каждую точку некоторой области пространства) проходит одна
- произвольные постоянные, соответствует двухпараметрическое семейство кривых такое, что через каждую точку пространства (по крайней мере, каждую точку некоторой области пространства) проходит одна
из кривых этого семейства. Множествам  и
и 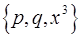 соответствуют свои два семейства кривых. Таким образом, систему координат
соответствуют свои два семейства кривых. Таким образом, систему координат 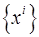 можно
можно
-14-
Подставив векторную функцию (5.16 a) в уравнение (5.12 a) и проинтегрировав его, получаем общее решение
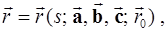 (5.18)
(5.18)
где 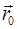 - произвольный постоянный вектор
- произвольный постоянный вектор
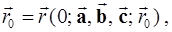
определяющий положение тройки векторов 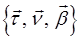 в пространстве при
в пространстве при 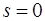 . Уравнения (5.18) являются параметрическими уравнениями кривой, проходящей через пространственную точку
. Уравнения (5.18) являются параметрическими уравнениями кривой, проходящей через пространственную точку 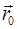 в направлении вектора
в направлении вектора 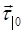 ортонормированной тройки векторов
ортонормированной тройки векторов 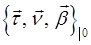 при
при 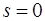 . Теорема доказана.
. Теорема доказана.