Способы перевода в двоичный код: http://videouroki.net/view_post.php?id=165
Особая значимость двоичной системы счисления в информатике определяется тем, что внутреннее представление любой информации в компьютере является двоичным, т.е. описываемым наборами только из двух знаков (0 и 1).
Конкретизируем описанный выше способ в случае перевода чисел из десятичной системы в двоичную. Целая и дробная части переводятся порознь. Для перевода целой части (или просто целого) числа необходимо разделить ее на основание системы счисления и продолжать делить частные от деления до тех пор, пока частное не станет равным 0. Значения получившихся остатков, взятые в обратной последовательности, образуют искомое двоичное число.
Например:
Остаток
25 : 2 = 12 (1),
12 : 2 = 6 (0),
6 : 2 = 3 (0),
3 : 2 = 1 (1),
1 : 2 = 0 (1).
Таким образом : 25(10)=11001(2).
Для перевода дробной части (или числа, у которого «0» целых) надо умножить ее на 2. Целая часть произведения будет первой цифрой числа в двоичной системе. Затем, отбрасывая у результата целую часть, вновь умножаем на 2 и т.д. Заметим, что конечная десятичная дробь при этом вполне может стать бесконечной {периодической) двоичной. Например:
0,73 • 2 = 1,46 (целая часть 1),
0,46 • 2 = 0,92 (целая часть 0 ),
0,92 • 2 = 1,84 (целая часть 1),
0,84 • 2 = 1,68 (целая часть 1) и т.д.
В итоге
0,73(10) =0,1011...(2).
Над числами, записанными в любой системе счисления, можно; производить различные арифметические операции. Так, для сложения и умножения двоичных чисел необходимо использовать табл. 1.5.
Таблица 2.2. Таблицы сложения и умножения в двоичной системе
| + | * | |||||
Заметим, что при двоичном сложении 1 + 1 возникает перенос единицы в старший разряд - точь-в-точь как в десятичной арифметике:
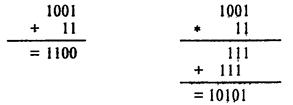
Пример: Перевести данное число из десятичной системы счисления в двоичную:
а) 464(10); б) 380,1875(10); в) 115,94(10) (получить пять знаков после запятой в двоичном представлении).
Решение.
464 | 0 380 | 0 |1875 115 | 1 |94
232 | 0 190 | 0 0|375 57 | 1 1|88
116 | 0 95 | 1 0|75 28 | 0 1|76
58 | 0 47 | 1 1|5 14 | 0 1|52
а) 29 | 1 б) 23 | 1 1|0 в) 7 | 1 1|04
14 | 0 11 | 1 3 | 1 0|08
7 | 1 5 | 1 1 | 1 0|16
3 | 1 2 | 0
1 | 1 1 | 1
а) 464(10) = 111010000(2); б) 380,1875(10) = 101111100,0011(2); в) 115,94(10) » 1110011,11110(2) (в настоящем случае было получено шесть знаков после запятой, после чего результат был округлен).
ВОСЬМЕРИЧНАЯ И ШЕСТНАДЦАТИРИЧНАЯ СИСТЕМЫ СЧИСЛЕНИЯ
С точки зрения изучения принципов представления и обработки информации в компьютере, обсуждаемые в этом пункте системы представляют большой интерес.
Хотя компьютер «знает» только двоичную систему счисления, часто с целью уменьшения количества записываемых на бумаге или вводимых с клавиатуры компьютера знаков бывает удобнее пользоваться восьмеричными или шестнадцатиричными числами, тем более что, как будет показано далее, процедура взаимного перевода чисел из каждой из этих систем в двоичную очень проста - гораздо проще переводов между любой из этих трех систем и десятичной.
Перевод чисел из десятичной системы счисления в восьмеричную производится (по аналогии с двоичной системой счисления) с помощью делений и умножений на 8. Например, переведем число 58,32(10):
58 : 8 = 7 (2 в остатке),
7 : 8 = 0 (7 в остатке).
0,32 • 8 = 2,56,
0,56 • 8 = 4,48,
0,48-8=3,84,...
Таким образом, 58,32(10) =72,243... (8) (из конечной дроби в одной системе может получиться бесконечная дробь в другой).
Перевод чисел из десятичной системы счисления в шестнадцатеричную производится аналогично.
С практической точки зрения представляет интерес процедура взаимного преобразования двоичных, восьмеричных и шестнадцатиричных чисел. Для этого воспользуемся табл. 1.6 чисел от 0 до 15 (в десятичной системе счисления), представленных в других системах счисления.
Для перевода целого двоичного числа в восьмеричное необходимо разбить его справа налево на группы по 3 цифры , а затем каждой группе поставить в соответствие ее восьмеричный эквивалент. Например:
11011001= 11011001, т.е. 11011001(2) =331(8).
Заметим, что группу из трех двоичных цифр часто называют «двоичнойтриадой».
Перевод целого двоичного числа в шестнадцатиричное производится путем разбиения данного числа на группы по 4 цифры - «двоичныететрады»:
1100011011001 = 1 1000 1101 1001, т.е. 1100011011001(2)= 18D9(16).
Для перевода дробных частей двоичных чисел в восьмеричную или шестнадцатиричную системы аналогичное разбиение на триады или тетрады производится от точки вправо (с дополнением недостающих последних цифр нулями):
0,1100011101(2) =0,110 001 110 100 = 0,6164(8),
0,1100011101(2) = 0,1100 0111 0100 = 0,C74(16).
Перевод восьмеричных (шестнадцатиричных) чисел в двоичные производится обратным путем - сопоставлением каждому знаку числа соответствующей тройки (четверки) двоичных цифр.
Таблица 2.3 Соответствие чисел в различных системах счисления
| Десятичная | Шестнадцатиричная | Восьмеричная | Двоичная |
| А | |||
| В | L011 | ||
| С | |||
| D | |||
| E | |||
| F |
Преобразования чисел из двоичной в восьмеричную и шестнадцатиричную системы и наоборот столь просты (по сравнению с операциями между этими тремя системами и привычной нам десятичной) потому, что числа 8 и 16 являются целыми степенями числа 2. Этой простотой и объясняется популярность восьмеричной и шестнадцатиричной систем в вычислительной технике и программировании. Если необходимо перевести число из двоичной системы счисления в систему счисления, основанием которой является степень двойки, достаточно объединить цифры двоичного числа в группы по столько цифр, каков показатель степени, и использовать приведенный ниже алгоритм. Например, если перевод осуществляется в восьмеричную систему, то группы будут содержать три цифры (8 = 23). Итак, в целой части будем производить группировку справа налево, в дробной — слева направо. Если в последней группе недостает цифр, дописываем нули: в целой части — слева, в дробной — справа. Затем каждая группа заменяется соответствующей цифрой новой системы. Соответствия приведены в таблицах.
| P | |||||
| P | |||||||||
| P | |||||||||||||||||
| A | B | C | D | E | F |
Для выполнения арифметических операций в системе счисления с основанием P необходимо иметь соответствующие таблицы сложения и умножения.
Пример:
1. Сложить числа:
а) 10000000100(2) + 111000010(2) = 10111000110(2).
б) 223,2(8) + 427,54(8) = 652,74(8).
в) 3B3,6(16) + 38B,4(16) = 73E,A(16).
10000000100 223,2 3B3,6
+ 111000010 + 427,54 +38B,4
------------ ------- -----
10111000110 652,74 73E,A
2. Выполнить вычитание:
а) 1100000011,011(2) - 101010111,1(2) = 110101011,111(2).
б) 1510,2(8) - 1230,54(8) = 257,44(8).
в) 27D,D8(16) - 191,2(16) = EC,B8(16).
1100000011,011 1510,2 27D,D8
- 101010111,1 -1230,54 -191,2
-------------- ------- ------
110101011,111 257,44 EC,B8
3. Выполнить умножение:
а) 100111(2) ´ 1000111(2) = 101011010001(2).
б) 1170,64(8) ´ 46,3(8) = 57334,134(8).
в) 61,A(16) ´ 40,D(16) = 18B7,52(16).
100111 1170,64 61,A
*1000111 * 46,3 *40,D
------------- -------------- ----------
100111 355 234 4F 52
+ 100111 + 7324 70 + 1868
100111 47432 0 ----------
100111 ------------- 18B7,52
------------- 57334,134
Арифметические действия с числами в шестнадцатиричной системе счисления выполняются по аналогии с двоичной и десятичной системами. Для этого необходимо воспользоваться соответствующими таблицами.
Рассмотрим еще один возможный способ перевода чисел из одной позиционной системы счисления в другую - метод вычитания степеней. В этом случае из числа последовательно вычитается максимально допустимая степень требуемого основания, умноженная на максимально возможный коэффициент, меньший основания; этот коэффициент и является значащей цифрой числа в новой системе. Например, число 114(10):
114 - 26 = 114 – 64 = 50,
50 - 25 = 50 – 32 = 18,
18 - 24 = 2,
2 - 21 = 0.
Таким образом, 114(10) = 1110010(2).
114 – 1 ∙ 82 = 114 – 64 = 50,
50 – 6 ∙ 81 = 50 – 48 = 2,
2 – 2 ∙ 8° = 2 – 2 = 0.
Итак, 114(10)= 162(8).