Дерево достижимости

Дерево достижимости (другое название покрывающее дерево) представляет все достижимые маркировки сети Петри, а также – все возможные последовательности запусков её переходов.

Для любой сети данный граф конечен и может быть построен с помощью следующей процедуры:

1.Первоначально предполагается, что дерево содержит единственную вершину корень М₀ и не имеет дуг.

2.Пусть М – вершина дерева, которая еще не объявлена листом (т.е. вершиной, из которой не исходит ни одна дуга), но в дереве нет исходящих из нее дуг. Возможны четыре случая:

а). Ни один из переходов сети не может сработать при разметке М. В этом случае вершина М объявляется листом.

б). На пути из корня дерева в вершину М существует вершина М ’ такая, что М = М ’. Вершина М объявляется листом.

в). На пути из корня дерева в вершину М существует вершина М ‘ такая, что М’<М. Для любого места р такого, что М’(р)<М(р), значение, соответствующей координаты М заменяется на w и вершина М объявляется w-листом.

г). Если ни один из вышеперечисленных случаев не имеет места, то М – внутренняя вершина дерева. Для каждого перехода t Î T такого, что М £ F(p_j, t) , в дерево добавляется новая вершина

M’(p_j) = M(p_j) - F(p_j, t) + F(t, p_j), p_j Î P,

ведущая из М в М’, помеченная символом t.

 

Пример 2.3. Построим дерево достижимости для сети, рассмотренной в примере 2.1. (рис.2.6):

 

 

 

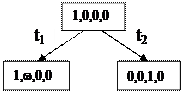Рис.2.6. Дерево достижимости в примере 2.3.

 

Построенное дерево позволяет зафиксировать неограниченность только одного места в данной сети – р_2, однако граф разметок указывает на наличие, так называемой, вторичной неограниченности, то есть ограниченности, проявляющейся как результат неограниченности других мест. В данном случае это неограниченность места р₄.

Чтобы иметь возможность устанавливать вторичную неограниченность необходимо построить полное дерево достижимости сети Петри по следующей процедуре:

1. Строится дерево достижимости сети À. Если это дерево не имеет w-листов, то построение полного дерева закончено и оно совпадает с деревом достижимости.

2. Если дерево достижимости содержит w-лист М, то для него строится дерево достижимости для сети À’, полученной из À заменой начальной разметки М₀ на разметку М. При этом правила срабатывания переходов и изменения разметки сети обобщаются на случай векторов с w с учетом арифметических свойств расширенного множества натуральных чисел. Построенное дерево присоединяется к основному дереву совмещением корня М в новом дереве с листом М в основном дереве. Процесс повторяется до тех пор, пока не исчезнет последний w-лист.

Полное дерево достижимости для рассмотренного выше примера 2.3 представлено на рис.2.7:

 

 

 

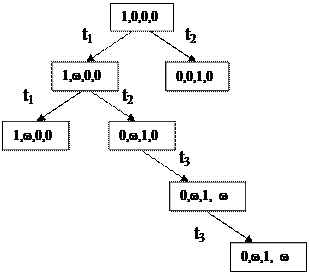Рис.2.7. Полное дерево достижимости в примере 2.3.

 

Конечная цель специальной теории сетей Петри - автоматический анализ свойств сетей, их автоматический синтез и преобразование, на основе которых могут быть построены практические алгоритмы анализа, синтеза и преобразований дискретных систем.