рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Науковедение
- /
- Планирование первого порядка
Реферат Курсовая Конспект
Планирование первого порядка
Планирование первого порядка - раздел Науковедение, Статистические методы планирования Представление Неизвестной Функции Отклика (12.1) Полиномом Является Наиболее ...
Представление неизвестной функции отклика (12.1) полиномом является наиболее удобным. На первой стадии исследования обычно принимают полином первой степени. Так для трехфакторной задачи теоретическое уравнение регрессии в этом случае имеет вид
 (12.2)
(12.2)
Уравнение регрессии, получаемое на основании результатов эксперимента, в отличие от приведенного выше теоретического уравнения, имеет вид

 (12.3)
(12.3)
где коэффициенты регрессии  являются оценками для теоретических коэффициентов регрессии
являются оценками для теоретических коэффициентов регрессии , т.е.
, т.е.
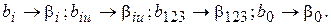
Выбор основных факторов и их уровней. В качестве факторов можно выбирать только контролируемые и управляемые переменные, т.е. такие, которые исследователь может поддерживать постоянными в течение каждого опыта на заданных уровнях. В число факторов должны быть включены параметры процесса, оказывающие наиболее сильное влияние на функцию отклика. Для выяснения наиболее важных факторов анализируется априорная информация, ранее проведенные аналитические и экспериментальные исследования. При необходимости с этой целью проводят специальные опыты, получившие название «отсеивающий эксперимент».
Для каждого фактора надо указать тот интервал изменения параметров, в пределах которого ставится исследование. Для этого на основе априорной информации устанавливаются ориентировочные значения факторов (при оптимизации они выбираются так, чтобы их комбинации давали наилучший результат или близ кий к нему). Этой комбинации значений факторов соответствует многомерная точка в факторном пространстве, которая и принимается за исходную точку при построении плана эксперимента. Координаты этой точки называют основными (нулевыми) уровнями факторов.
кий к нему). Этой комбинации значений факторов соответствует многомерная точка в факторном пространстве, которая и принимается за исходную точку при построении плана эксперимента. Координаты этой точки называют основными (нулевыми) уровнями факторов.
Интервалом варьирования факторов называется некоторое число (свое для каждого фактора), прибавление которого к основному уровню дает верхний, а вычитание – нижний уровни фактора. Этот интервал принимается за единицу нового масштаба измерения фактора. Для упрощения записи условий эксперимента и обработки экспериментальных данных масштабы по осям выбираются так, чтобы верхний уровень соответствовал +1, нижний – 1, а основной соответствовал 0.
Для факторов с непрерывной областью определения это достигается с помощью формулы преобразования
 (12.4)
(12.4)
где xi– кодированное значение фактора; 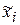 – значение фактора в натуральных единицах;
– значение фактора в натуральных единицах;  – значение основного уровня в натуральных единицах;
– значение основного уровня в натуральных единицах;  – единица масштаба (интервал варьирования); i – номер фактора.
– единица масштаба (интервал варьирования); i – номер фактора.
Выбор интервалов варьирования производится на основе опыта и интуиции исследователя. При этом следует учитывать точность фиксирования факторов, оценивать силу влияния фактора на отклик у, погрешность измерения величины у. Все это поможет избежать ситуации, при которой интервал варьирования окажется недостаточным для того, чтобы уловить изменение у.
Важно учитывать характер решаемой задачи. При решении: задачи оптимизации стремятся выбрать для первой серии экспериментов такую единицу масштаба, которая давала бы возможность для шагового движения к оптимуму. При описании процесса единица масштаба должна охватывать всю область, подлежащую описанию интерполяционным полиномом.
Минимально необходимое число уровней факторов на единицу больше порядка интерполяционного полинома. Поскольку результаты наблюдений отклика носят случайный характер, приходится в каждой точке плана проводить m параллельных опытов (обычно m = 2 ÷ 4), осреднение результатов которых дает возможность уменьшить погрешность оценки истинного значения отклика в  раз. Эксперимент делится на m серий опытов. В каждой серии последовательность опытов рандомизируется, т.е. с помощью таблицы случайных чисел определяется случайная последовательность реализации опытов в каждой серии. Рандомизация: позволяет ослабить или исключить вовсе влияние неконтролируемых случайных или систематических погрешностей на результаты исследования.
раз. Эксперимент делится на m серий опытов. В каждой серии последовательность опытов рандомизируется, т.е. с помощью таблицы случайных чисел определяется случайная последовательность реализации опытов в каждой серии. Рандомизация: позволяет ослабить или исключить вовсе влияние неконтролируемых случайных или систематических погрешностей на результаты исследования.
Полный факторный эксперимент (ПФЭ). Полным факторным экспериментом называется эксперимент, реализующий все возможные неповторяющиеся комбинации уровней независимых факторов, каждый из которых варьируется на двух уровнях. Число этих комбинаций равно 2N. Нахождение уравнения регрессии методом ПФЭ состоит из: а) планирования эксперимента; б) собственно эксперимента; в) проверки воспроизводимости (однородности выборочных дисперсий); г) получения уравнения регрессии с проверкой статистической значимости коэффициентов регрессии; д) проверки адекватности уравнения регрессии.
Таблица 12.3
| № точки плана (v) | 
| 
| 
| 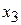
| 
| 
| 
| 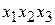
| Отклик |
| +1 | -1 | -1 | -1 | +1 | +1 | +1 | -1 | у1 | |
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | у2 | |
| +1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | у3 | |
| +1 | +1 | +1 | -1 | +1 | -1 | -1 | -1 | у4 | |
| +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | у5 | |
| +1 | +1 | -1 | +1 | -1 | +1 | -1 | -1 | у6 | |
| +1 | -1 | +1 | +1 | -1 | -1 | +1 | -1 | у7 | |
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | у8 |
Условия эксперимента записывают в виде матрицы планирования. Пример матрицы планирования для трех факторов дан в табл. 12.3. Здесь столбцы х1, х2, х3 образуют матрицу плана. Эти столбцы задают планирование – по ним определяются условия опытов. Последующие столбцы матрицы получаются перемножением соответствующих значений факторов х1, х2, х3. В матрицу добавляется еще один столбец – фиктивная переменная х0 для расчета свободного члена b0 в уравнении регрессии. Значение х0 одинаково во всех строчках и равно +1.
Матрицу плана можно представить геометрически (рис. 12.4). Условия проведения опытов соответствуют координатам вершин куба, центром которого является основной уровень, а ребра соответственно параллельны координатным осям, их длина равна. двум интервалам. Номера вершин куба соответствуют номерам точек в матрице планирования.

Рис. 12.4. Геометрическое изображение полного факторного эксперимента 23
Можно наглядно показать, что точность определения уравнения регрессии с использованием методов ПЭ выше. Иллюстрируем сказанное примером. Пусть требуется найти коэффициенты регрессии b0 и b1 уравнения y = b0 + b1x по двум опытам. При одинаковых погрешностях с увеличением интервала или радиуса области изменения фактора х точность определения коэффициентов регрессии растет. Перенесем этот принцип повышения точности линейного уравнения регрессии на многофакторные процессы. Это можно сделать двумя путями. Первый путь – увеличение интервалов варьирования по каждому фактору (точно так же, как и в однофакторном процессе). Однако в многофакторном пространстве есть еще один принципиально иной путь увеличения радиуса области изменения факторов – путь одновременного варьирования уровней всех факторов без увеличения интервала каждого фактора. Рассмотрим, что это дает при N = 2 (при –1, +1). Опыты, спланированные по методике однофакторного эксперимента, в факторном пространстве, очевидно, будут представлены точками (0, +1), (0, –1), ( + 1, 0), (–1, 0) (рис. 12.5), лежащими на осях x1 и x2.
Если же изменить значения уровней факторов одновременно,, то точки плана, построенного в соответствии с концепцией многофакторного эксперимента, расположатся в вершинах внешнего квадрата (+1, +1), (–1, +1), (–1, –1), (+1, –1) (рис. 8.5). Ясно, что при этом исследованная область изменения факторов будет больше. Отметим, что этот эффект тем ощутимее, чем больше размерность N факторного пространства. В самом деле, при планировании по методике однофакторного эксперимента опорные точки всегда располагаются на концах хорд длиной 2 единицы, при многофакторном планировании опорные точки располагаются на концах диаметров, длина которых  2 , т. е. в
2 , т. е. в  раз больше.
раз больше.
При N = 2 построение матриц ПФЭ не вызывает затруднений, при увеличении же числа факторов возникает необходимость в некоторых специальных приемах построения матриц. Рассмотрим два наиболее простых приема. Первый прием основан на правиле чередования знаков. В первом столбце знаки чередуются поочередно, во втором – через 2, в третьем – через 4, в четвертом – через 8, в пятом – через 16 и т.д. по степеням двойки. Второй прием основан на последовательном достраивании матрицы. Для этого при добавлении нового фактора необходимо повторить комбинации уровней исходного плана сначала при значении нового фактора на верхнем уровне, а затем – на нижнем.
Матрицы ПФЭ обладают рядом свойств, делающих их оптимальным средством получения уравнения регрессии по результатам эксперимента. Для любого числа факторов коэффициенты будут вычисляться по формуле
 (12.5)
(12.5)
где i = 0, 1, 2,.., N – номер фактора; - средний отклик по m опытам в точке с номером v (здесь j – номер параллельного опыта в точке v); k – число опытов в матрице.
- средний отклик по m опытам в точке с номером v (здесь j – номер параллельного опыта в точке v); k – число опытов в матрице.
Планирование эксперимента исходит из статистического характера зависимостей, поэтому полученные уравнения связи подвергаются тщательному статистическому анализу с целью извлечь из результатов эксперимента максимум информации и убедиться в достоверности полученной зависимости и ее точности.
Каждый эксперимент несет в себе какую-то погрешность, для повышения надежности производят повторения опытов при тех же условиях, т.е. повторяют для каждой строки таблицы планирования.
Построчные дисперсии подсчитывают по формуле
 (12.6)
(12.6)
где m – число повторных опытов в точках плана.
Дисперсия отклика s2{y} есть среднеарифметическая дисперсий всех k различных вариантов опытов:
 (12.7)
(12.7)
Прежде чем производить объединение дисперсий, надо убедиться в их однородности. Проверка производится с помощью критериев Фишера и Кохрэна. Гипотеза об однородности дисперсий принимается, если экспериментальное значение критерия Кохрэна или Фишера не превышает табличного значения.
Далее на основе метода наименьших квадратов находится уравнение регрессии, после чего предстоит выполнить статистические оценки полученного уравнения.
Проверка значимости каждого коэффициента проводится независимо. Для этого можно использовать проверку по t-критерию Стьюдента. Прежде всего, находят дисперсию коэффициента регрессии. При равномерном дублировании опытов по точкам с числом повторных опытов т она определяется по формуле
 (12.8)
(12.8)
Далее рассчитываются значения ti-критерия. Если ti>tкр, то коэффициент bi признается значимым, в противном случае bi считается статистически незначимым, т.е. bi = 0. После этого уравнение регрессии составляется в виде уравнения связи выходного параметра у и переменных хi , включающего только значимые коэффициенты.
После вычисления коэффициентов уравнения необходимо прежде всего проверить его пригодность или адекватность. Для этого достаточно оценить отклонение выходной величины у, предсказанной уравнением регрессии, от результатов эксперимента у в различных точках факторного пространства.
Рассеяние результатов эксперимента относительно уравнения связи, аппроксимирующего искомую функциональную зависимость, можно охарактеризовать с помощью остаточной дисперсии или дисперсии адекватности  , оценка которой, справедливая при равном числе дублирующих опытов, находится по формуле
, оценка которой, справедливая при равном числе дублирующих опытов, находится по формуле
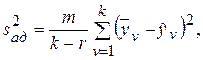 (12.9)
(12.9)
где r – число членов аппроксимирующего полинома.
Проверка адекватности состоит в выяснении соотношения между дисперсией адекватности  и дисперсией воспроизводимости s2{y} и проводится с использованием критерия Фишера F, который в данном случае формируется как отношение
и дисперсией воспроизводимости s2{y} и проводится с использованием критерия Фишера F, который в данном случае формируется как отношение  Если вычисленное значение критерия меньше критического Fкр для соответствующих степеней свободы
Если вычисленное значение критерия меньше критического Fкр для соответствующих степеней свободы 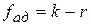 и
и 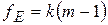 при заданном уровне значимости a, то описание признается адекватным объекту.
при заданном уровне значимости a, то описание признается адекватным объекту.
Дробный факторный эксперимент. Во многих практических задачах взаимодействия второго и высших порядков отсутствуют или пренебрежимо малы. Кроме того, на первых этапах исследования часто нужно получить в первом приближении лишь линейную аппроксимацию изучаемого уравнения связи при минимальном числе экспериментов. Поэтому использовать полный факторный эксперимент для определения коэффициентов лишь при линейных членах и парных произведениях неэффективно из-за реализации большого числа опытов (2N), особенно при большом числе факторов N. При увеличении числа независимых переменных N число опытов (число точек в плане) растет по показательной функции, т.е. число оцениваемых коэффициентов N+1 становится меньше числа точек плана 2N, в результате чего остается излишне много степеней свободы на проверку гипотезы адекватности. Разность  будет в этом случае характеризовать избыточность плана; например,
будет в этом случае характеризовать избыточность плана; например,  при N = 2;
при N = 2;  при N = 4;
при N = 4; 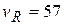 уже при N = 6 и т.д.
уже при N = 6 и т.д.
Полная матрица планирования (см. табл. 12.3) позволяет рассчитать восемь коэффициентов уравнения. Если есть основания считать, что в выбранных интервалах варьирования процесс может быть описан линейной зависимостью, то достаточно определить четыре коэффициента b0, b1 ,b2 , и b3 уравнения
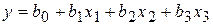 . (12.13)
. (12.13)
Для решения этой задачи можно ограничиться четырьмя опытами, если в планировании ПФЭ для двух факторов (22) использовать столбец табл. 8.5 x1 x2 в качестве плана для х3 (табл. 8.6).
Таблица 12.5 Таблица 12.6
| v | x0 | x1 | x2 | х3 |
| +1 | -1 | -1 | +1 | |
| +1 | +1 | -1 | -1 | |
| +1 | -1 | +1 | -1 | |
| +1 | +1 | +1 | +1 |
| v | x0 | x1 | x2 | x1x2 |
| +1 | -1 | -1 | +1 | |
| +1 | +1 | -1 | -1 | |
| +1 | -1 | +1 | -1 | |
| +1 | +1 | +1 | +1 |
Такой сокращенный план – половина ПФЭ 23 – носит название полуреплики от ПФЭ 23. Пользуясь таким планированием, можно определить свободный член и три коэффициента уравнения регрессии при линейных членах.
Если коэффициенты регрессии при парных произведениях не равны нулю, то найденные коэффициенты b будут смешанными оценками для теоретических коэффициентов  :
:
 (12.14)
(12.14)
Таким образом, сокращение числа опытов приводит к получению смешанных оценок для коэффициентов. Для того чтобы определить, какие теоретические коэффициенты смешаны, удобно пользоваться таким приемом: поставив 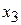 на место
на место  , получим соотношение
, получим соотношение 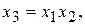 называемое генерирующим соотношением. После умножения его на х3 получаем
называемое генерирующим соотношением. После умножения его на х3 получаем  . Учитывая, что
. Учитывая, что  (х3 равняется
(х3 равняется 


 + 1 или –1), получаем
+ 1 или –1), получаем
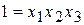 . (12.16)
. (12.16)
Это произведение носит название определяющего контраста; с его помощью удобно определять, в каких столбцах содержатся одинаковые элементы, т.е. какие коэффициенты смешаны.
Умножив по очереди определяющий контраст на х1, х2, х3 найдем
 .
.
Полученным соотношениям соответствует система смешанных оценок (8.14), т.е.  смешан с
смешан с  .
.
При использовании дробного факторного эксперимента (ДФЭ) необходимо иметь четкое представление о так называемой разрешающей способности дробной реплики, т. е. определить заранее, какие коэффициенты являются несмешанными оценками для соответствующих теоретических коэффициентов. Тогда в зависимости от поставленной задачи подбирается дробная реплика, с помощью которой можно извлечь максимальную информацию из эксперимента. Например, в задаче с четырьмя факторами (N = 4) в качестве генерирующего соотношения можно взять 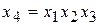 или любой из эффектов двойного взаимодействия, например
или любой из эффектов двойного взаимодействия, например  .
.
Воспользовавшись определяющим контрастом  , получим такую систему смешанных оценок:
, получим такую систему смешанных оценок:

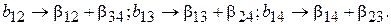
В реальных задачах тройные взаимодействия бывают равными нулю значительно чаще, чем двойные. Значит, если нас более всего по физическому смыслу задачи интересуют оценки для линейных эффектов, следует выбирать генерирующее соотношение  .
.
При генерирующем соотношении  определяющий контраст выражается соотношением
определяющий контраст выражается соотношением 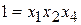 . Получается следующая система оценок
. Получается следующая система оценок

Следовательно, дробную реплику с генерирующим соотношением  имеет смысл использовать, если нас более всего интересуют коэффициенты
имеет смысл использовать, если нас более всего интересуют коэффициенты 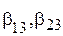 и
и  .- Применяют дробные реплики и большей степени дробности (1/8 реплики, 1/4 реплики и т.п.).
.- Применяют дробные реплики и большей степени дробности (1/8 реплики, 1/4 реплики и т.п.).
Дробные реплики позволяют резко сократить число экспериментов для описания процесса. Следует иметь в виду, однако, что применение ДФЭ имеет весьма серьезный недостаток – исключаются из исследования некоторые взаимодействия факторов. Как правило, весьма затруднительно даже в практически известных процессах априорно установить отсутствие взаимодействия факторов. Поэтому использование ДФЭ, особенно большой дробности, требует весьма осторожного подхода.
Рассмотрим пример использования дробного факторного эксперимента. Исследования тепло-массообмена при конденсации химически реагирующего газа на основе теории подобия показали, что процесс можно описать уравнением подобия вида
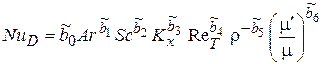 , (12.17)
, (12.17)
где NuD – диффузионное число Нуссельта; члены в правой части характеризуют влияние отдельных факторов на процесс (Аr – свободной конвекции, Sc – переносных свойств газовой смеси, Кх – кинетики химических реакций, ReT – отводимого теплового потока, r – концентрации неконденсируемого газа,  – трения на границе раздела жидкой и газообразной фаз).
– трения на границе раздела жидкой и газообразной фаз).
Для определения коэффициентов уравнения применим метод планирования. Прологарифмировав (8.17) и перейдя от натуральных значений факторов
 к кодированным значениям xi согласно формуле преобразования (12.4), получим следующее линейное уравнение регрессии процесса:
к кодированным значениям xi согласно формуле преобразования (12.4), получим следующее линейное уравнение регрессии процесса:
 , (12.18)
, (12.18)
где  .
.
Поскольку зависимость (12.18) линейная, для определения величин b0 и bi можно составить ортогональный план первого порядка на основе 1/8 реплики ПФЭ для шести факторов с числом опытов, равным 26-3=8. При этом будем использовать следующие генерирующие соотношения: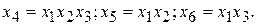 Матрица планирования приведена в табл. 8.7.
Матрица планирования приведена в табл. 8.7.
Таблица 12.7
| v | x0 | x1 | x2 | x3 | x4 | x5 | x6 | y |
| + | - | - | - | - | + | + | y1 | |
| + | + | - | - | - | - | - | y2 | |
| + | - | + | - | + | - | + | y3 | |
| + | + | + | - | - | + | - | y4 | |
| + | - | - | + | + | + | - | y5 | |
| + | + | - | + | - | - | + | y6 | |
| + | - | + | + | - | - | - | y7 | |
| + | + | + | + | + | + | + | y8 |
Проведение опытов, обработка опытных данных с целью получения коэффициентов уравнения (12.18) и их статистический анализ выполняются в такой же последовательности, как и в предыдущем примере.
– Конец работы –
Эта тема принадлежит разделу:
Статистические методы планирования
Статистические методы планирования... Планирование первого порядка...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Планирование первого порядка
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов