рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Науковедение
- /
- Модифицированный метод Хука-Дживса
Реферат Курсовая Конспект
Модифицированный метод Хука-Дживса
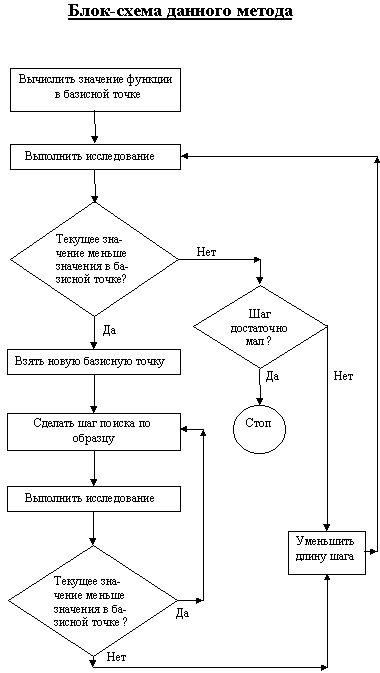
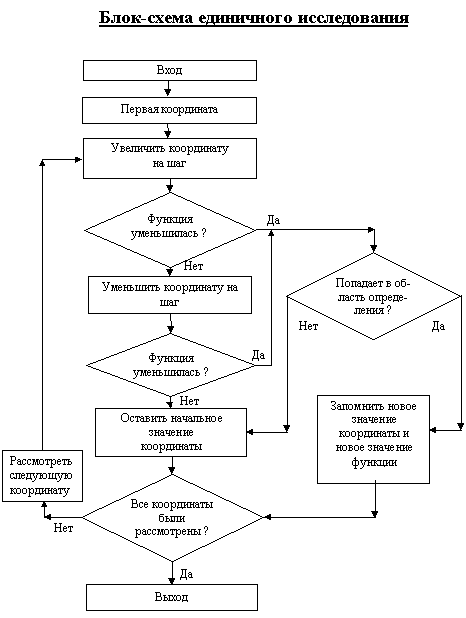
Модифицированный метод Хука-Дживса - раздел Науковедение, Блок-схема единичного исследования Этот Метод Нетрудно Модифицировать И Для У...
Этот метод нетрудно модифицировать и для учета ограничений .Было выдвинуто предложение , что для этого будет вполне достаточно при решении задачи минимизации присвоить целевой функции очень большое значение там,где ограничения нарушаются .К тому же такую идею просто реализовать с помощью програмирования .
Нужно проверить ,каждая ли точка ,полученная в процессе поиска , принадлежит области ограничений .Если каждая , то целевая функция вычисляется обычным путем . Если нет , то целевой функции присваивается очень большое значение . Таким образом , поиск будет осуществляться снова в допустимой области в направлении к минимальной точке внутри этой области.
В тексте прогаммы модифицированного метода прямого поиска Хука-Дживса сделана попытка реализовать такую процедуру. Рассматриваемая задача формулируется следующим образом :
минимизировать f (x1,x2) = 3x12+4x1x2+5x22 ,
при ограничениях x1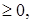 x2
x2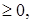 x1+x2
x1+x2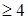 .
.
Текст программы
program HuDjMody;
(*** Модифицированный метод Хука-Дживса ***)
(*** (при наличии ограничений) ***)
uses crt;
label 0,1,2,3,4,5,6,7;
var k,h,z,ps,bs,fb,fi :real;
i,j,n,fe :integer;
x,y,b,p :array[1..10] of real;
(*** Процедура,вычисляющая функцию ***)
procedure calculate;
begin
z:=3*sqr(x[1])+(4*x[1]*x[2])+(5*sqr(x[2]));
if (x[1]<0) or (x[2]<0) or ((x[1]+x[2])<4) then
z:=1.7e+38;
fe:=fe+1; (*** Счетчик ***)
end;
begin
clrscr;
gotoxy(20,2);
writeln('Модифицированный метод Хука-Дживса');
gotoxy(23,3);
writeln('( при наличии ограничений )');
writeln;
writeln('Введите число переменных:');
readln(n);
writeln;
writeln('Введите начальную точку x1,x2,…,xN');
for i:=1 to n do
readln(x[i]);
writeln;
writeln('Введите длину шага');
readln(h);
writeln;
k:=h;
fe:=0;
for i:=1 to n do
begin
y[i]:=x[i];
p[i]:=x[i];
b[i]:=x[i];
end;
calculate;
fi:=z;
writeln('Начальное значение функции', z:2:3);
for i:=1 to n do
writeln(x[i]:2:3);
ps:=0;
bs:=1;
(*** Исследование вокруг базисной точки ***)
j:=1;
fb:=fi;
0: x[j]:=y[j]+k;
calculate;
if z<fi then goto 1;
x[j]:=y[j]-k;
calculate;
if z<fi then goto 1;
x[j]:=y[j];
goto 2;
1: y[j]:=x[j];
2: calculate;
fi:=z;
writeln('Пробный шаг',' ', z:2:3);
for i:=1 to n do
writeln(x[i]:2:3);
if j=n then goto 3;
j:=j+1;
goto 0;
3: if fi<fb-1e-08 then goto 6;
(*** После оператора 3,если функция не уменьшилась, ***)
(*** произвести поиск по образцу ***)
if (ps=1) and (bs=0) then
goto 4;
(*** Но если исследование производилось вокруг точки ***)
(*** шаблона PT,и уменьшение функции не было достигнуто,***)
(*** то изменить базисную точку в операторе 4: ***)
(*** в противном случае уменьшить длину шага в операторе***)
(*** 5: ***)
goto 5;
4: for i:=1 to n do
begin
p[i]:=b[i];
y[i]:=b[i];
x[i]:=b[i];
end;
calculate;
bs:=1;
ps:=0;
fi:=z;
fb:=z;
writeln('Замена базисной точки',' ',z:2:3);
for i:=1 to n do
writeln(x[i]:1:3);
(*** (следует за последним комментарием) ***)
(*** и провести исследование вокруг новой базисной точки ***)
j:=1;
goto 0;
5: k:=k/10;
writeln('Уменьшить длину шага');
if k<1e-08 then goto 7;
(*** Если поиск незакончен,то произвести новое ***)
(*** исследование вокруг новой базисной точки ***)
j:=1;
goto 0;
(*** Поиск по образцу ***)
6: for i:=1 to n do
begin
p[i]:=2*y[i]-b[i];
b[i]:=y[i];
x[i]:=p[i];
y[i]:=x[i];
end;
calculate;
fb:=fi;
ps:=1;
bs:=0;
fi:=z;
writeln('Поиск по образцу',' ',z:2:3);
for i:=1 to n do
writeln(x[i]:2:3);
(*** После этого произвести исследование вокруг ***)
(*** последней точки образца ***)
j:=1;
goto 0;
7: writeln('Минимум найден');
for i:=1 to n do
writeln('x(',i,')=',p[i]:2:3);
writeln;
writeln('Минимум функции равен',' ',fb:2:3);
writeln('Количество вычислений функции равно',' ',fe);
repeat until keypressed;
end.
Приведенная выше программа реализует описанную процедуру. Одной или двух точек бывает недостаточно для определения начальной точки. Первая точка всегда должна выбираться осмотрительно. ЭВМ работает только с ограниченной точностью, и ошибки могут накапливаться в процессе сложных вычислений, особенно если шаг имеет “неудобную” длину. (Обычно мы будем избегать “неудобной” длины, но программа должна быть работоспособна и в таких ситуациях.) Поэтому в строке , где выясняется вопрос об изменении базисной точки, мы избегаем уменьшения длины шага из-за накапливания ошибки введением длины шага, равной 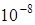 . Мы отслеживаем, где производится исследование – в базисной точке (В5 = 1, Р5 = 0) или в точке образца (В5 = 0, Р5 = 1). Как можно убедиться на практике, если не принимаются такие меры предосторожности даже программа с удовлетворительной логикой будет неработоспособна.
. Мы отслеживаем, где производится исследование – в базисной точке (В5 = 1, Р5 = 0) или в точке образца (В5 = 0, Р5 = 1). Как можно убедиться на практике, если не принимаются такие меры предосторожности даже программа с удовлетворительной логикой будет неработоспособна.
В приведенной программе минимальная длина шага равна 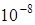 , но она может быть изменена . Для контроля за выполнением процедуры в программу введена печать промежуточных результатов. Для увеличения скорости счета могут быть удалены строки вывода подсказок и пояснений.
, но она может быть изменена . Для контроля за выполнением процедуры в программу введена печать промежуточных результатов. Для увеличения скорости счета могут быть удалены строки вывода подсказок и пояснений.
Процедура calculate вычисляет значение минимизируемой функции ,в нашем случае : f (x1,x2) = 3x12+4x1x2+5x22 ,
при ограничениях x1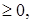 x2
x2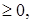 x1+x2
x1+x2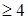 .
.
Минимум, равный 44, достигается в точке (3;1) при ограничении x1+x2=4.
Для начальной точки (4;3) и при длине шага , равной единице , программой успешно решена задача минимизации .
Ниже приведена распечатка результата работы программы :
Модифицированный метод Хука-Дживса
(при наличииограничений)
Введите число переменных
Введите начальную точку х1,х2,…,хN
Введите длину шага
Начальное значение функции 141.000
4.000
3.000
Пробный шаг 108.000
3.000
3.000
Пробный шаг 71.000
3.000
2.000
Поиск по образцу 1.70000000000001566Е+0038
2.000
1.000
Пробный шаг 44.000
3.000
1.000
Пробный шаг 44.000
3.000
1.000
Поиск по образцу 1.70000000000001566Е+0038
3.000
0.000
Пробный шаг 48.000
4.000
0.000
Пробный шаг 48.000
4.000
0.000
Замена базисной точки 44.000
3.000
1.000
Пробный шаг 44.000
3.000
1.000
Пробный шаг 44.000
3.000
1.000
Уменьшить длину шага
Пробный шаг 44.000
3.000
1.000
Пробный шаг 44.000
3.000
1.000
Уменьшить длину шага
Пробный шаг 44.000
3.000
1.000
Пробный шаг 44.000
3.000
1.000
Уменьшить длину шага
Пробный шаг 44.000
3.000
1.000
Пробный шаг 44.000
3.000
1.000
Уменьшить длину шага
Пробный шаг 44.000
3.000
1.000
Пробный шаг 44.000
3.000
1.000
Уменьшить длину шага
Пробный шаг 44.000
3.000
1.000
Пробный шаг 44.000
3.000
1.000
Уменьшить длину шага
Пробный шаг 44.000
3.000
1.000
Пробный шаг 44.000
3.000
1.000
Уменьшить длину шага
Пробный шаг 44.000
3.000
1.000
Пробный шаг 44.000
3.000
1.000
Уменьшить длину шага
Минимум найден
х(1) = 3.000
х(2) = 1.000
Минимум функции равен 44.000
Количество вычислений равно 74
Для начальной точки (3;4) и длины шага , равной единице , программой также успешно решена задача минимизации .
Для начальной точки (5;6) и длины шага , равной единице , задача не решена , т.к. программа остановилась в точке (1;3) , т.е. на активном ограничении , и выдала неверный результат .
Распечатка результата работы программы приведена ниже :
Модифицированный метод Хука-Дживса
(при наличииограничений)
Введите число переменных
Введите начальную точку х1,х2,…,хN
Введите длину шага
Начальное значение функции 375.000
5.000
6.000
Пробный шаг 324.000
4.000
6.000
Пробный шаг 253.000
4.000
5.000
Поиск по образцу 155.000
3.000
4.000
Пробный шаг 124.000
2.000
4.000
Пробный шаг 81.000
2.000
3.000
Поиск по образцу 1.70000000000001566Е+0038
0.000
1.000
Пробный шаг 1.70000000000001566Е+0038
0.000
1.000
Пробный шаг 1.70000000000001566Е+0038
0.000
1.000
Замена базисной точки 81.000
2.000
3.000
Пробный шаг 60.000
1.000
3.000
Пробный шаг 60.000
1.000
3.000
Поиск по образцу 1.70000000000001566Е+0038
0.000
3.000
Пробный шаг 60.000
1.000
3.000
Пробный шаг 60.000
1.000
3.000
Замена базисной точки 60.000
1.000
3.000
Пробный шаг 60.000
1.000
3.000
Пробный шаг 60.000
1.000
3.000
Уменьшить длину шага
Пробный шаг 60.000
1.000
3.000
Пробный шаг 60.000
1.000
3.000
Уменьшить длину шага
Пробный шаг 60.000
1.000
3.000
Пробный шаг 60.000
1.000
3.000
Уменьшить длину шага
Пробный шаг 60.000
1.000
3.000
Пробный шаг 60.000
1.000
3.000
Уменьшить длину шага
Пробный шаг 60.000
1.000
3.000
Пробный шаг 60.000
1.000
3.000
Уменьшить длину шага
Пробный шаг 60.000
1.000
3.000
Пробный шаг 60.000
1.000
3.000
Уменьшить длину шага
Пробный шаг 60.000
1.000
3.000
Пробный шаг 60.000
1.000
3.000
Уменьшить длину шага
Пробный шаг 60.000
1.000
3.000
Пробный шаг 60.000
1.000
3.000
Уменьшить длину шага
Минимум найден
х(1) = 1.000
х(2) = 3.000
Минимум функции равен 60.000
Количество вычислений равно 89
Аналогичные неутешительные результаты были получены для начальной точки (5;6) и длины шага , равной 0.5 .Неверное решение было найдено в точке (1.5;2.5) . Для начальной точки (4;3) и длины шага , равной 0.5 ,программа работала нормально , но было получено неверное решение в точке (2.5;1.5) .
Проблема понятна . С помощью данного метода невозможно двигаться вдоль границы области ограничений и сходимость достигается в первой же точке границы , где и находится решение . Общая задача оптимизации при наличии ограничений очень сложна и для получения практического метода решения требуются более изощренные процедуры , чем приведенная выше .
Литература:
1. Б.Банди “Методы оптимизации”
2. Р.Хук , Т.А.Дживс “ Прямой поиск решения для числовых и статических проблем ”, 212-219 с., 1961 .
– Конец работы –
Эта тема принадлежит разделу:
Блок-схема единичного исследования
Методы Хука Дживса... Содержание...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Модифицированный метод Хука-Дживса
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов