Статистические ряды распределения
При проведении серии испытаний экспериментальные данные (выборка) представляются в виде табл.4.1, которая называется простым статистическим рядом.
Таблица 4.1
Простой статистический ряд
| Номера испытаний | … | i | … | n | |||
Варианты признака 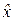
| x1 | x2 | x3 | … | xi | … | xn |
Если элементы случайной выборки упорядочены по возрастанию, т.е.
x1 £ x2 £ x3 £…£ xi £…£ xn,
получаемая таблица называется вариационным рядом. Разность wn = xn – x1 между наибольшим и наименьшим элементами вариационного ряда называется размахом выборки.
Вариационный ряд является простейшей формой статистического закона распределения, который определяется в результате эксперимента.
Если наблюдаемый случайный признак является дискретным, или точность измерений ограничена, или результаты наблюдений округляются, значения некоторых вариантов признака в выборке могут совпадать. Множества совпадающих вариантов наблюдаемого признака называются связками. Из этого следует, что различные варианты могут появляться с разной частотой.
Таблица 4.2
Вариационный ряд с вариантами различной частоты
Варианты признака 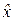
| x1 | x2 | x3 | … | xl | … | xn |
| Частота вариантов | m1/n | m2/n | m3/n | … | ml/n | … | mn/n |
В табл. 4.2 представлен вариационный ряд, в котором ml – число появлений в выборке варианта xl; 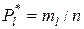 – частота варианта xl,
– частота варианта xl, 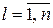 . Такой ряд можно рассматривать как ряд распределения некоторой дискретной случайной величины.
. Такой ряд можно рассматривать как ряд распределения некоторой дискретной случайной величины.
Пример 4.1. Проведены испытания 12 однотипных микросхем и с точностью до 1 часа зарегистрировано время безотказной работы каждой из них. Результаты испытаний сведены в простой статистический ряд.
Таблица 4.3
Простой статистический ряд (к примеру 4.1)
| i | ||||||||||||
| ti, ч |
На основе простого статистического ряда, табл.4.3, построен вариационный ряд.
Таблица 4.4
Вариационный ряд (к примеру 4.1)
| l | ||||||||||||
| tl, ч |
Массив данных в табл. 4.4 может быть представлен вариационным рядом с частотами вариантов.
Таблица 4.5
Вариационный ряд с частотами вариантов (к примеру 4.1)
| tl, ч | ||||||||||
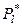
| 1/12 | 2/12 | 1/12 | 1/12 | 2/12 | 1/12 | 1/12 | 1/12 | 1/12 | 1/12 |
Из табл.4.5 видно, что в выборке содержатся две связки, в каждую из которых входит два варианта.
По распределению величины 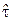 – времени безотказной работы микросхем, можно судить о распределении генеральной совокупности, тем точнее и надёжнее, чем больше объём n выборки.
– времени безотказной работы микросхем, можно судить о распределении генеральной совокупности, тем точнее и надёжнее, чем больше объём n выборки.
При большом объёме выборки из генеральной совокупности, наблюдаемый признак которой имеет непрерывное распределение, вариационный ряд (табл. 4.2) становится громоздким. В этом случае диапазон наблюдаемых вариантов xi разбивают на интервалы, называемые разрядами, вычисляют частоты  попадания вариантов случайной величины
попадания вариантов случайной величины 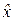 в эти разряды и представляют результаты в виде табл. 4.6. Эта таблица называется интервальным вариационным или статистическим рядом случайной величины
в эти разряды и представляют результаты в виде табл. 4.6. Эта таблица называется интервальным вариационным или статистическим рядом случайной величины 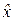 .
.
Таблица 4.6
Интервальный вариационный ряд
| Jl | x1; x2 | x2; x3 | … | xl; xl+1 | … | xr; xr+1 |
| ml | m1 | m2 | … | ml | … | mr |
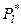
| 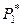
| 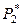
| … | 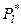
| … | 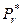
|
В представленной таблице Jl = [xl; xl+1) – l-й разряд; ml – число значений (вариантов) случайной величины 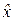 , попавших в l-й разряд; xl; xl+1 – границы l-го разряда; r – число разрядов;
, попавших в l-й разряд; xl; xl+1 – границы l-го разряда; r – число разрядов; 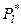 = ml/n = P*(xl £ xi< xl+1),
= ml/n = P*(xl £ xi< xl+1), 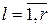 .
.
Число r разрядов, на которые разбивается случайная выборка, не должно быть слишком большим. В этом случае частоты подвергаются незакономерным колебаниям и статистический ряд становится невыразительным. Указанное число не должно быть и слишком малым, так как описание распределения случайной величины становится грубым. Чем однороднее статистический материал и чем больше его объём, тем большее число разрядов можно выбирать. Для ориентировочного определения числа разрядов можно пользоваться соотношениями
r » 5 lg n или 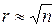 .
.
При этом целесообразно, чтобы выполнялись условия 5 < r < 25, ml ³ 5, 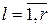 . Длины разрядов можно брать как одинаковыми, так и различными. В последнем случае статистическая обработка экспериментальных данных несколько усложняется, однако при значительной неравномерности распределения наблюдаемой случайной величины в областях её наибольшей изменчивости разряды целесообразно делать более короткими.
. Длины разрядов можно брать как одинаковыми, так и различными. В последнем случае статистическая обработка экспериментальных данных несколько усложняется, однако при значительной неравномерности распределения наблюдаемой случайной величины в областях её наибольшей изменчивости разряды целесообразно делать более короткими.
Примечание. Если наблюдаемый признак 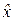 представляет собой дискретную случайную величину, то статистический ряд её распределения может иметь лишь форму табл.4.2. Для такого признака интервальный статистический ряд лишён физического смысла.
представляет собой дискретную случайную величину, то статистический ряд её распределения может иметь лишь форму табл.4.2. Для такого признака интервальный статистический ряд лишён физического смысла.
Пример 4.2. Проведены испытания 100 однотипных микросхем и зарегистрировано время безотказной работы каждой из них в часах. Результаты испытаний сведены в табл.4.7.
Таблица 4.7
Результаты испытаний микросхем (к примеру 4.2)
| i | ti | i | ti | i | ti | i | ti | i | ti |
| 151,5 | 151,5 | 2,0 | 105,0 | 21,1 | |||||
| 190,0 | 38,5 | 56,2 | 30,0 | 107,8 | |||||
| 67,2 | 190,0 | 211,4 | 73,3 | 111,0 | |||||
| 38,5 | 46,0 | 151,5 | 138,8 | 123,8 | |||||
| 281,0 | 301,7 | 40,2 | 84,3 | 301,7 | |||||
| 156,4 | 261,2 | 114,1 | 33,0 | 13,1 | |||||
| 38,5 | 40,2 | 3,0 | 3,9 | 8,5 | |||||
| 18,6 | 120,3 | 212,0 | 190,0 | 105,0 | |||||
| 34,4 | 26,3 | 114,1 | 96,7 | 241,4 | |||||
| 58,2 | 63,3 | 51,3 | 267,0 | 18,6 | |||||
| 18,5 | 105,0 | 177,4 | 494,8 | 75,3 | |||||
| 49,5 | 30,0 | 30,0 | 105,0 | 24,5 | |||||
| 204,3 | 156,2 | 73,2 | 33,0 | 13,1 | |||||
| 65,2 | 67,2 | 107,8 | 46,0 | 67,2 | |||||
| 86,7 | 89,1 | 71,2 | 27,8 | 123,8 | |||||
| 107,8 | 386,2 | 102,2 | 9,5 | 86,7 | |||||
| 43,2 | 58,2 | 40,2 | 54,2 | 230,3 | |||||
| 21,1 | 34,4 | 120,3 | 5,8 | 167,1 | |||||
| 107,8 | 75,3 | 26,3 | 40,2 | 34,4 | |||||
| 7,2 | 221,1 | 63,3 | 22,3 | 117,2 |
На основе статистического материала табл.4.7 построен интервальный вариационный ряд, который приведён в табл.4.8.
Таблица 4.8
Интервальный вариационный ряд (к примеру 4.2)
| Jl | 0; 50 | 50; 100 | 100; 150 | 150; 200 | 200; 250 |
| ml | |||||
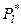
| 0,38 | 0,21 | 0,18 | 0,1 | 0,06 |
| Jl | 250; 300 | 300; 350 | 350; 400 | 400; 450 | 450; 500 |
| ml | |||||
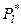
| 0,03 | 0,02 | 0,01 | 0,00 | 0,01 |
Для большей наглядности ряд может оформляться графически в виде полигона. При его построении определяются «представители» разрядов ряда распределения, т.е. их средние точки с абсциссами
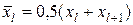 ,
, 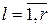 .
.
Из этих точек восстанавливаются перпендикуляры, длины которых равны частотам 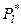 . Описанный переход от вариационного ряда к статистическому можно интерпретировать как переход к новой дискретной случайной величине
. Описанный переход от вариационного ряда к статистическому можно интерпретировать как переход к новой дискретной случайной величине 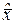 , принимающей значения
, принимающей значения 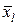 с «вероятностями»
с «вероятностями» 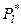 .
.
Совокупность точек А1, А2,…, Ar, которые лежат на верхних концах перпендикуляров, называется огивой распределения случайной величины 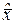 [9]. Соединив смежные точки огивы отрезками прямых, получим полигон распределения случайной величины
[9]. Соединив смежные точки огивы отрезками прямых, получим полигон распределения случайной величины 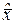 , который является полной аналогией многоугольника распределения. На рис.4.1 изображён полигон, который построен на основании статистического материала примера 4.2.
, который является полной аналогией многоугольника распределения. На рис.4.1 изображён полигон, который построен на основании статистического материала примера 4.2.
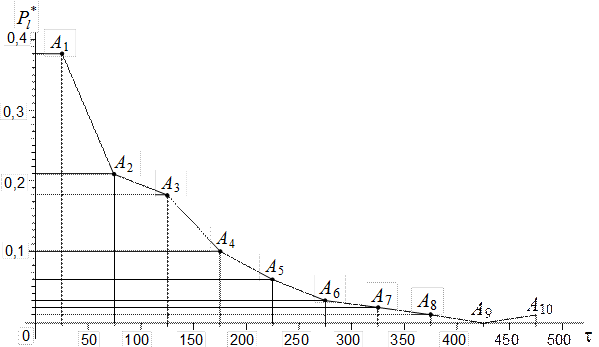
Рис.4.1. Полигон распределения (к примеру 4.2)