Выборочная функция распределения
По вариационному ряду табл.4.2 можно построить статистическую или выборочную функцию распределения 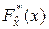 случайной величины
случайной величины 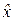 .
.
По определению
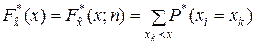 .
.
Следовательно, в явном виде статистическая функция распределения примет вид
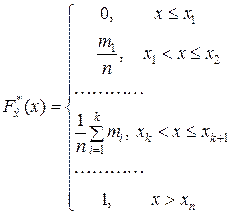 . (4.3.1)
. (4.3.1)
График функции (4.3.1) в условиях примера 4.1 показан на рис.4.4. Обоснованием применимости функции 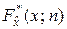 для оценивания истинной функции распределения
для оценивания истинной функции распределения 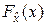 случайной величины
случайной величины 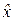 служит предельная теорема В.И. Гливенко, которая формулируется следующим образом.
служит предельная теорема В.И. Гливенко, которая формулируется следующим образом.
При увеличении объёма n выборки статистическая функция распределения 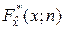 неограниченно приближается (сходится по вероятности) к истинной функции распределения
неограниченно приближается (сходится по вероятности) к истинной функции распределения 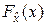 случайной величины
случайной величины 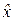 :
:
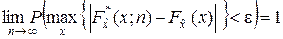 ,
, 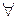 e > 0. (4.3.2)
e > 0. (4.3.2)
Таким образом, 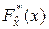 – состоятельная оценка
– состоятельная оценка 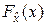 . Известно также, что функция
. Известно также, что функция 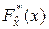 является несмещённой оценкой для
является несмещённой оценкой для 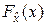 :
:
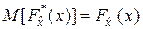 .
.
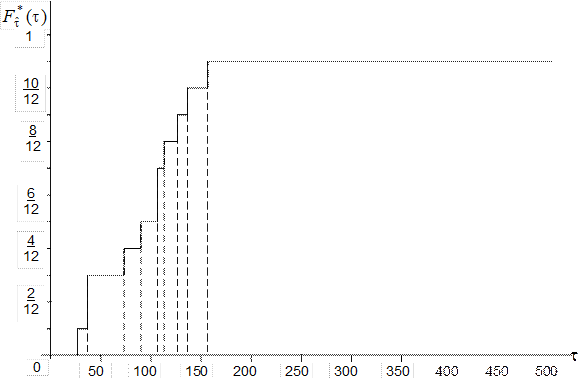
Рис.4.4. Статистическая функция распределения (к примеру 4.1)
В силу соотношения (4.3.2) дисперсия 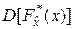 с ростом n уменьшается, следовательно, эта оценка является асимптотически эффективной. Отсюда вытекает, что при достаточно большом массиве экспериментальных данных функцию распределения изучаемой случайной величины можно приближённо заменять её выборочной функцией распределения.
с ростом n уменьшается, следовательно, эта оценка является асимптотически эффективной. Отсюда вытекает, что при достаточно большом массиве экспериментальных данных функцию распределения изучаемой случайной величины можно приближённо заменять её выборочной функцией распределения.