Линейная модель наблюдения

Рассматриваемый ниже метод наименьших квадратов при линейной модели наблюдения получил название схемы Гаусса–Маркова.

Пусть наблюдаемые параметры и параметры искомой функциональной зависимости связаны линейным уравнением, а ошибки наблюдения аддитивны, причём имеют равные нулю математические ожидания:

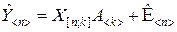, (8.3.1)

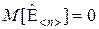, (8.3.2)

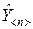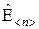где X_[n;k] – прямоугольная матрица, называемая матрицей наблюдения; и , как и ранее, соответственно случайные векторы наблюдения и ошибок наблюдения.

На основании равенства (8.3.2) можно записать

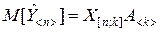. (8.3.3)

В модели Гаусса–Маркова предполагается, что относительно вектора 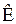известна некоторая дополнительная информация. Рассмотрим возможные варианты использования данной информации.

Один из наиболее простых случаев тот, когда известно, что наблюдения некоррелированы и равноточны. В этом варианте корреляционная матрица вектора 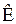или, что то же самое, вектора выражается формулой

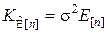, (8.3.4)

где s² – дисперсия наблюдения; E_[n] – единичная матрица.

Дисперсия наблюдения может быть и неизвестной, тогда она подлежит оценке наряду с компонентами вектора A. При неизвестной дисперсии s² не представляется возможным получить какие-либо характеристики точности оценивания.

Более общим является случай, когда наблюдения коррелированны и равноточны, однако для них известна только нормированная корреляционная матрица G_[n], а корреляционная матрица вектора 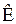имеет вид

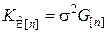, (8.3.5)

причём s² – в общем случае неизвестная дисперсия наблюдения.

Покажем, что модель наблюдения (8.3.3), (8.3.4) легко сводится к модели (8.3.3), (8.3.5). Из линейной алгебры известно, что любая симметричная положительно-определённая матрица (а матрица G является таковой) может быть представлена в виде

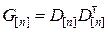, (8.3.6)

где 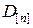– невырожденная матрица.

Произведём замену переменных по формуле

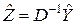, (8.3.7)

тогда

.

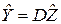Корреляционная матрица вектора 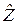вычисляется следующим образом: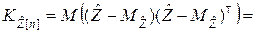

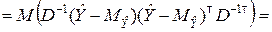
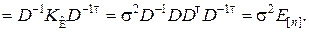
Получили выражение, аналогичное выражению (8.3.4).

Условное уравнение (8.3.3) с учётом (8.3.7) приобретает вид

.

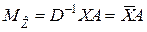Таким образом, модель наблюдения (8.3.3), (8.3.5) с помощью невырожденного линейного преобразования сводится к соотношениям

, , .

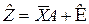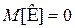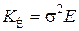Это и есть исходная модель наблюдения.

Если наблюдения коррелированы и неравноточны, то корреляционная матрица ошибок наблюдения

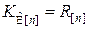, (8.3.8)

где 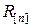– известная симметричная положительно-определённая матрица, которая, как и матрица G в формуле (8.3.5), может быть представлена в виде произведения двух невырожденных квадратных матриц аналогично равенству (8.3.6). Это означает, что преобразованием, аналогичным преобразованию (8.3.7), модель наблюдения (8.3.3), (8.3.8) сводится к исходной модели.

По этим причинам в данном подразделе детально рассматривается только наиболее простая модель наблюдения (8.3.3), (8.3.4), а в конце его с помощью преобразования типа (8.3.6) получаются аналогичные результаты для схем наблюдения с корреляционными матрицами ошибок (8.3.5) и (8.3.8).