Нормальные уравнения и оценки наименьших квадратов
Для линейной модели наблюдения (8.3.1) квадратичная функция (8.2.6), при минимизации которой отыскиваются оценки компонентов вектора A, будет иметь вид
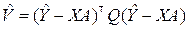, (8.3.9)
а нормальные уравнения (8.2.9) – вид
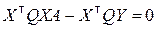. (8.3.10)
Можно показать, что система нормальных уравнений (8.3.10) всегда совместна [10]. Будем считать, что матрица X имеет ранг k (предполагается, что n ³ k), а матрица весов Q – невырожденная. Тогда матрица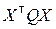 
будет невырожденной, а потому из равенства (8.3.10) можно получить выражение для оценки вектора A:
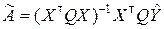. (8.3.11)
Если весовая матрица единичная (Q = E), то вместо соотношения (8.3.11) получим равенство
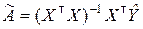. (8.3.12)
Если относительно вектора ошибок ничего не известно, то ничего нельзя сказать и о свойствах оценок (8.3.11) или (8.3.12). Если же соотношение (8.3.2) выполняется, то оценки (8.3.11), (8.3.12) являются несмещёнными. Действительно
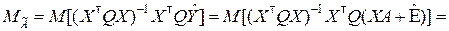
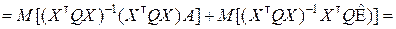
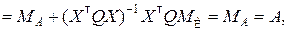
поскольку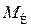 
= 0.
Пусть корреляционная матрица вектора ошибок наблюдений имеет вид (8.3.4). Вычислим корреляционную матрицу вектора оценок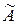 
. Обозначим
; 
.
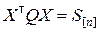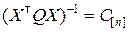В этих обозначениях формула для МНК-оценки (8.3.11) перепишется в виде
,
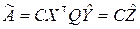где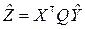 
.
Тогда корреляционная матрица вектора оценок 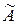вычисляется по формуле
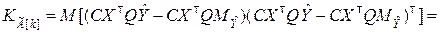
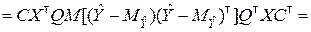(8.3.13)
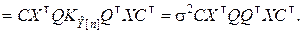
В процессе преобразований в выражении (8.3.13) учтено, что
, 
.
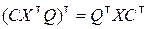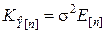Если Q = E, то
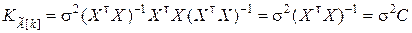. (8.3.14)
На практике наиболее часто используется вариант МНК-оценивания, при котором в качестве весовой матрицы Q выбирается матрица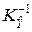 
, поскольку в таком случае МНК-оценка получается эффективной. Доказательство этого факта можно найти, например, в [10]. Для такого варианта корреляционная матрица оценки вычисляется по формуле
,
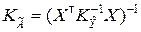которая при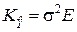 
совпадает с выражением (8.3.14).
Когда величина s2 известна, формулы (8.3.13), (8.3.14) позволяют отыскать корреляционную матрицу вектора 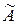. Из данных формул следует, что даже при некоррелированных равноточных наблюдениях компоненты вектора оценок оказываются коррелированными. Для их некоррелированности необходима ещё ортогональность столбцов матрицы наблюдений X (при Q = E) или столбцов матрицы 
в общем случае.
Если дисперсия наблюдений s2 неизвестна, её необходимо оценить наряду с компонентами вектора A, иначе невозможно отыскать корреляционную матрицу вектора 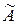, которая даёт характеристики точности оценивания.
Покажем, каким образом можно получить оценку величины s2. В математической статистике доказывается, что остаточная сумма квадратов
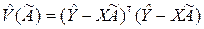(8.3.15)
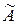(– МНК-оценка при линейной модели наблюдения) имеет закон распределения 
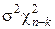, если вектор ошибок наблюдения 
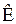характеризуется корреляционной матрицей s2E (n – размерность вектора 
, k – число оцениваемых параметров).
В скалярной форме выражение (8.3.15) имеет вид
.
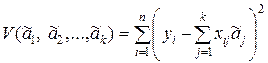На основании свойств 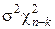- распределения получается, что
,
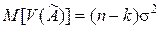а потому оценку для величины s2 можно приближённо вычислять по формуле
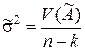. (8.3.16)
Отметим, что это оценка несмещённая.
Без доказательства укажем, что МНК-оценки не всегда получаются эффективными. Ранее уже отмечалось со ссылкой на работу [10], что свойством эффективности обладают МНК-оценки для моделей наблюдения (8.3.3), (8.3.4) при Q = E, (8.3.3), (8.3.5) при Q = G–1 и (8.3.3), (8.3.8) при Q = R–1. Это следует, в частности, для нормального распределения вектора ошибок из эффективности оценок, получаемых по методу максимального правдоподобия, поскольку МНК и ММП-оценки совпадают при указанном способе выбора весовых матриц. При всех остальных способах выбора матрицы весов МНК-оценки неэффективны. Однако это не означает, что варианты выбора матрицы весов Q, приводящие к неэффективным оценкам, нецелесообразны. Различные соображения могут привести к выбору матрицы весов в другой форме.
П р и м е р 8.2. Известно, что величина a – постоянная, схема оценивания имеет вид
, 
,
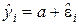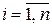где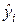 
– наблюдаемая величина, 
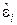– ошибка наблюдения. Требуется по результатам наблюдения определить оценку величины a с использованием МНК, а также получить характеристики точности оценивания при известных моментных характеристиках ошибки :
, 
, .
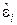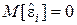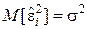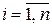Данная задача совпадает с задачей из примера 8.1, однако там ничего не говорилось о статистических свойствах ошибок измерения .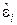
▼ Случайную величину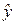 
представим в виде вектора
.
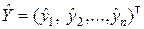Роль вектора оцениваемых параметров играет скалярная величина a, т.е. k = 1. Поэтому матрица X, имеющая размерность n´k, представляет собой вектор-столбец, состоящий из единиц:
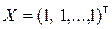
В качестве матрицы весов Q выбираем единичную матрицу E[n]. МНК-оценку скалярной величины a вычисляем по формуле (8.3.12). Предварительно найдём матрицы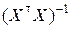 
и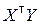 
:
;
;
.
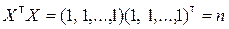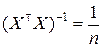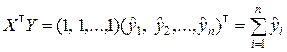Окончательно получим
.
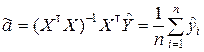Заметим, что решение совпадает с полученным в примере 8.1.
Эта оценка является несмещённой и эффективной. Определим точность оценки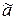 
. На основании формулы (8.3.14) получим
,
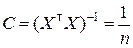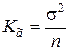. (8.3.17)
Если бы величина s2 не была априори известной, то её оценку можно было бы получить на основании формулы (8.3.16):
.
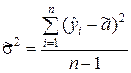Затем можно найти дисперсию оценки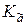 
по формуле (8.3.17) с заменой s2 на 
.
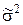Данный пример фактически указывает, каким образом следует оценивать математическое ожидание случайной величины и каковы при этом точечные характеристики этих оценок. Напомним, что ранее тот же результат для оценки математического ожидания был получен с помощью предельных теорем.
▲
П р и м е р 8.3. Рассмотрим задачу, аналогичную приведённой в примере 8.2, с тем отличием, что независимые измерения величины a производятся с различной от эксперимента к эксперименту точностью, которая характеризуется дисперсией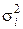 
, .
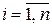▼ Итак, имеем схему неравноточных наблюдений:
; 
; 
.
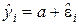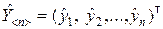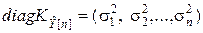Корреляционная матрица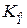 
взята в диагональной форму в силу независимости измерений.
Данную задачу сводим к предыдущей, используя преобразования (8.3.6), (8.3.7). При этом
,
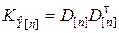где D – диагональная матрица с диагональю
.
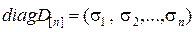Тогда формула (8.3.7) приводит к новому вектору
.
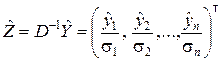Легко убедиться, что корреляционная матрица вектора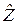 
получается при этом единичной, а задача сводится к предыдущей. Уравнение (8.3.3) записывается в виде
,
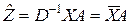где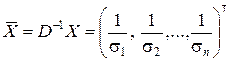 
.
Далее находим, как и в примере 8.2:
; 
; 
;
.
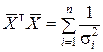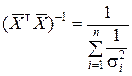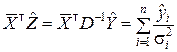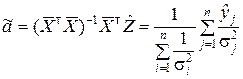Данная оценка является несмещённой и эффективной, причём
.
▲
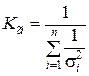Сравнивая полученное решение с решением задачи 8.1 или 8.2, видим, что учёт неравноточности измерений приводит к иному решению. Возвращаясь к замечанию, указанному в примере 8.1, можно опять же подчеркнуть, что учёт статистических свойств ошибок измерений приводит к необходимости иного выбора функции V(a), чем это было сделано в примере 8.1 или 8.2.