Выше 7‑го порядка

Индуктивное доказательство Голомба применимо к бесконечному числу рядов, чьи элементы удваиваются. В частности, после того как мы успешно покрыли доску 7×7, можно понять, как покрываются доски размером n×n, где n = 2k·7. К примеру, возьмем доску 14‑го порядка. Разобьем ее на области, расположив зачерненную доску 7‑го порядка в левом верхнем углу и положив одно тримино у нижнего правого угла этой зачерненной доски, подобно тому, как мы проделывали раньше (см. рис. 3, справа). Поскольку доску 7‑го порядка можно покрыть, из этого с очевидностью вытекает доказательство для доски 14‑го порядка, а далее, по индукции, доказательства для порядков 28, 56, 112…

Подобное доказательство нельзя вывести для доски 10‑го порядка, расположив в ее углу квадрат 5‑го порядка, поскольку его не всегда удается покрыть (см. рис. 4). Однако с этой сложностью легко справиться, применив несколько иной подход. Разместим в левом верхнем углу квадрат 8‑го порядка – его, как нам известно, можно покрыть. Остается угловая область, имеющая ширину 2 и занимающая низ и правую часть большого квадрата (см. рис. 7). Путем поворотов и отражений любую недостающую клетку в квадрате 8‑го порядка удается расположить в любом месте этой доски. Таким же образом получаем доказательство для порядков 20, 40, 80 и т. д. Сходное доказательство существует для доски 11‑го порядка: квадрат 7‑го порядка располагаем в ее углу, и тогда угловая область, занимающая нижнюю и боковую часть большого квадрата, будет иметь ширину 4. Индукция позволяет вывести доказательства и для порядков 22, 44, 88… Понятно, что эта методика дает нам бесконечное количество покрываемых досок, длина сторон которых удваивается (это своего рода удваивающийся ряд). Просто располагайте в левом верхнем углу любой доски заведомо покрываемый квадрат со стороной, которая меньше стороны исходной доски либо равна ей. Если оставшуюся снизу и сбоку область большой доски вам удастся покрыть – значит, и большая доска покрываема.

 

 

 

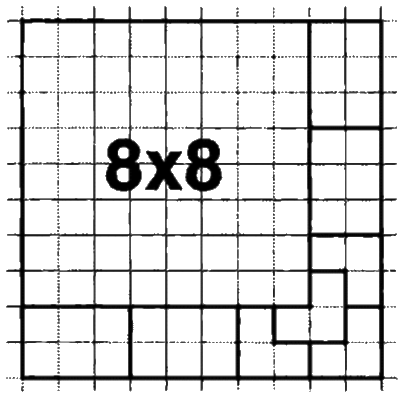
_{Рис. 7. Доску 19‑го порядка можно покрыть.}

Обычно труднее всего покрыть доски, у которых длина сторон – простое число. Проблему доски 17‑го порядка удается решить, поместив в ее угол квадрат со стороной 13 и оставив внизу и сбоку область шириной 4. Проблему доски 19‑го порядка – поместив в ее угол квадрат 14‑го порядка (доказательство его покрываемости основано, в свою очередь, на таком же свойстве квадрата 7‑го порядка) и получив угловую область шириной 5 (см. рис. 8).

 

 

 

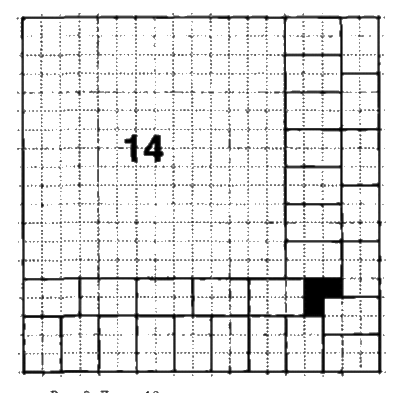
_{Рис. 8. Доску 19‑го порядка можно покрыть.}