рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Вид работы: Контрольные Работы
- /
- Задача. Исследовать средствами дифференциального исчисления функцию и построить ее график.
Реферат Курсовая Конспект
Задача. Исследовать средствами дифференциального исчисления функцию и построить ее график.
Задача. Исследовать средствами дифференциального исчисления функцию и построить ее график. - Контрольная Работа, раздел Образование, Методические указания и задания контрольных работ Решение. Исследование Будем Проводить По Следующей Схеме....
Решение. Исследование будем проводить по следующей схеме.
1. Область определения функции.
В нашем примере это множество всех действительных чисел,
т.е. x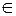 (–
(– ;+
;+ ).
).
2. Четность и нечетность функции.
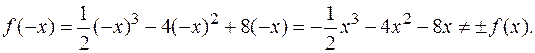
Функция не обладает свойствами четности или нечетности. Следовательно, график функции не будет симметричен ни относительно оси Oу, ни относительно начала координат.
3. Периодичность функции.
Данная функция непериодическая, так как является многочленом.
4. Непрерывность функции.
На всей области определения данная функция непрерывна как многочлен.
5. Поведение функции на концах области определения.
Концами области определения являются  и
и 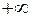 , так как
, так как 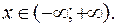 Найдем пределы функции при
Найдем пределы функции при 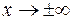 .
.
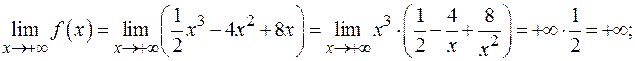
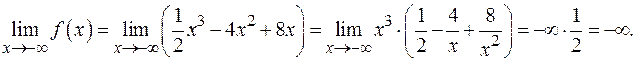
Таким образом, слева, при  , график функции уходит неограниченно вниз, а справа, при
, график функции уходит неограниченно вниз, а справа, при  , – неограниченно вверх.
, – неограниченно вверх.
6. Интервалы монотонности и точки экстремума.
Вычислим производную функции и найдем критические точки.
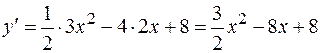 .
.
Производная существует при любых x.
Решим уравнение 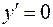 .
.
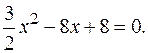
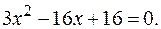

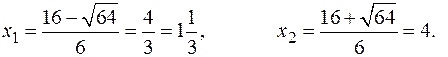
Следовательно,
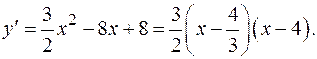
Точки  и
и  критические. Они делят область определения функции на интервалы:
критические. Они делят область определения функции на интервалы: 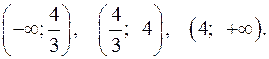 Изобразим эти интервалы на числовой оси (рис. 5).
Изобразим эти интервалы на числовой оси (рис. 5).
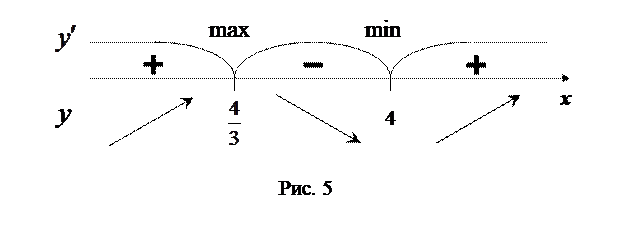
Поведение функции на каждом интервале определяется знаком производной. Для определения знака  на интервале достаточно взять любое значение х из рассматриваемого интервала и подставить его в производную
на интервале достаточно взять любое значение х из рассматриваемого интервала и подставить его в производную  .
.
а) На интервале  выберем число, например,
выберем число, например, 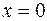 , и подставим его в производную:
, и подставим его в производную:  .
.
Так как на интервале  производная
производная  , следовательно, функция y возрастает на этом интервале (см. признаки монотонности).
, следовательно, функция y возрастает на этом интервале (см. признаки монотонности).
б) На интервале  возьмем
возьмем  , подставим в производную, получим
, подставим в производную, получим 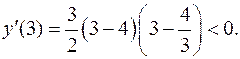 Следовательно, на интервале
Следовательно, на интервале  функция убывает.
функция убывает.
в) На интервале  возьмем значение
возьмем значение  . Видим, что
. Видим, что  следовательно, на интервале
следовательно, на интервале  функция возрастает.
функция возрастает.
Знаки первой производной проставим на рис. 5.
Замечаем, что при переходе через точку 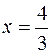 производная поменяла знак с плюса на минус, значит,
производная поменяла знак с плюса на минус, значит, 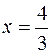 является точкой максимума (см. признак экстремума).
является точкой максимума (см. признак экстремума).
Найдем значение функции y в этой точке:

Таким образом, график имеет максимум в точке А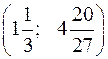 .
.
При переходе через точку 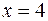 производная меняет знак с минуса на плюс (рис. 5). Это означает, что
производная меняет знак с минуса на плюс (рис. 5). Это означает, что 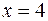 – точка минимума.
– точка минимума.
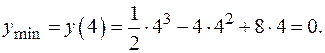
В точке B(4;0) график функции имеет минимум.
7. Интервалы выпуклости, вогнутости и точки перегиба.
Найдем производную второго порядка от рассматриваемой функции 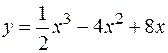 . Так как
. Так как 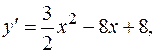 то
то 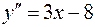 .
.
Вторая производная существует при любых значениях x.
Найдем точки, где  :
:
3x – 8 = 0  .
.
Значение 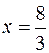 является единственным подозрительным на перегиб. Эта точка делит область определения
является единственным подозрительным на перегиб. Эта точка делит область определения 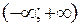 на интервалы
на интервалы  и
и  (рис. 6).
(рис. 6).
а) На интервале  выберем любое число, например,
выберем любое число, например, 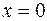 и подставим его во вторую производную
и подставим его во вторую производную 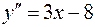 . Получим
. Получим 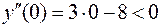 , значит, на интервале
, значит, на интервале  график функции выпуклый (см. признак выпуклости и вогнутости).
график функции выпуклый (см. признак выпуклости и вогнутости).
б) На интервале 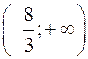 возьмем, например,
возьмем, например,  и подставим во вторую производную. Получим
и подставим во вторую производную. Получим  , значит, на интервале
, значит, на интервале 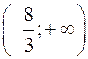 график функции вогнутый.
график функции вогнутый.
Знаки второй производной проставим на рис. 6.
 |

|
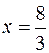 вторая производная
вторая производная  меняет знак, то
меняет знак, то 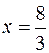 – точка перегиба (см. условие перегиба).
– точка перегиба (см. условие перегиба).
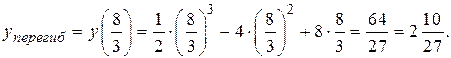
Таким образом, точка С – единственная точка перегиба.
– единственная точка перегиба.
8. Точки пересечения графика с осями координат.
На оси Oу 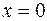 ,
, 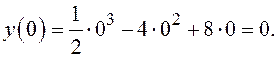 Получили точку пересечения с осью Oу: (0;0).
Получили точку пересечения с осью Oу: (0;0).
На оси Ox  , тогда
, тогда  ,
,
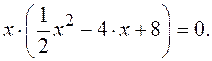
Произведение равно нулю, когда один из множителей равен нулю, в нашем случае 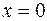 или
или 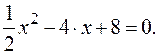
Решим квадратное уравнение: 
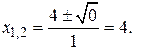
Значения функции в точках 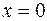 и
и 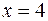 были найдены ранее:
были найдены ранее:
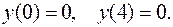
Таким образом, график функции пересекает ось Оx в точках (0;0) и (4;0).
9. Дополнительные точки.
Для более точного построения графика можно найти дополнительные точки. Например, найдем значение функции y при  :
:
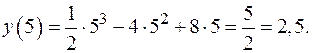
D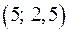 – дополнительная точка для построения графика.
– дополнительная точка для построения графика.
Выпишем результаты исследования функции 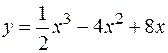 .
.
1. Область определения 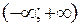 .
.
2. 
3. Функция возрастает на промежутках  и
и 
убывает на промежутке .
.
4. Максимум функции в точке А , минимум – в точке В(4;0).
, минимум – в точке В(4;0).
5. График выпуклый на интервале  и вогнутый на интервале
и вогнутый на интервале 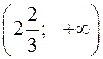 .
.
6. Точка перегиба С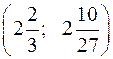 .
.
7. Точки пересечения с осями координат: (0;0), (4;0).
8. Дополнительная точка D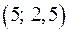 .
.
Построим график функции (рис. 7). На плоскости Oxy отметим все характерные точки: точки пересечения с осями координат, точки экстремумов, точку перегиба, а также дополнительную точку.
В силу непрерывности функции соединим все отмеченные точки плавной кривой, продолжив график влево вниз и вправо вверх согласно поведению функции на концах области определения и учитывая характер монотонности и выпуклости графика функции.
 |
Замечание.Графики многочленов представляют собой непрерывные линии, весьма разнообразные по форме. Они могут иметь различное количество точек экстремумов и перегибов, а также по-разному вести себя на бесконечности, т.е. при 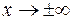 .
.
– Конец работы –
Эта тема принадлежит разделу:
Методические указания и задания контрольных работ
МАТЕМАТИКА... Методические указания и задания контрольных работ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Задача. Исследовать средствами дифференциального исчисления функцию и построить ее график.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?








Новости и инфо для студентов