Математичне сподівання
· Моменти та інші числові характеристики випадкових величин
· Дисперсія.
· Стандартне середньоквадратичне відхилення.
· Нормальний закон розподілу та його характеристики.
· Використання випадкових величин при обчисленні характеристик ризику.
· Двовимірні випадкові величини.
· Числові характеристики двовимірних випадкових величин
· Коефіцієнти варіації та кореляції.
· Функції розподілу двовимірних випадкових величин.
Математичним сподіванням М(Х) випадкової величини X називається число, яке обчислюється за формулою
М(Х) = Х1р(Х1) + Х2р(Х2) + ... + Хір(Хі). (1.4)
Для статистичного розподілу аналогічна характеристика положення центру розсіювання дається у вигляді середньої, х визначається за частотами або відносними частотами значень величини.
Із означення випливає, що математичне сподівання дискретної випадкової величини є невипадкова (постійна) величина. Це ж відноситься і до математичного сподівання неперервної випадкової величини.
Математичне сподівання числа появи події в одному випробуванні рівне ймовірності цієї події
Математичне сподівання неперервної величини визначається аналогічно, тільки замість простого сумування «зважених» по ймовірності значень величини тут доводиться застосовувати інтегрування. Враховуючи імовірнісний зміст щільності розподілу для неперервних випадкових величин математичне сподівання буде розраховуватися за формулою:
М(Х) = 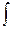 xf(x)dx (1.5)
xf(x)dx (1.5)
Із означення математичного сподівання випливають його властивості.
Математичне сподівання постійної величини С дорівнює самій цій постійній:
М(С) = С. (1.6)
Математичне сподівання перетину постійної величини з випадковою величиною дорівнює добутку постійної на математичне сподівання цієї випадкової величини.
М(С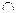 Х) = С М(Х) (1.7)
Х) = С М(Х) (1.7)
Для випадкових величин X і У справедливі співвідношення
М(Х± Y) = M(X)±M(Y).
Математичне сподівання лінійної функції Z = аХ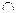 bY випадкової величини X дорівнює тій же лінійній функції від математичного сподівання величин X і Y:
bY випадкової величини X дорівнює тій же лінійній функції від математичного сподівання величин X і Y:
М(Y)=aM(X)+bM(Y)
Математичне сподівання перетину двох незалежних випадкових величин дорівнює добутку їх математичних сподівань.
Поряд з випадковою величиною X розглянемо її цілі степені: Математичне сподівання випадкової величини X* називають початковим моментом k-го порядку випадкової величини X. Таким чином, згідно означення
vk(X)= M(Xk)=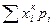 (1.8)
(1.8)
В якості характеристик положень центру групування розподілу поряд з числом М(Х) чи х інколи використовують ще дві характеристики: моду і медіану.
Модою дискретної випадкової величини називають найбільш ймовірне її значення (позначають символом т(Х)).
У статистичному розподілу під модою розуміють значення, що має найбільшу частоту.
Під медіаною розуміють значення x j  таблиці, що ділить її навпіл.
таблиці, що ділить її навпіл.
Важливу інформацію про випадкову величину дає ступінь чи масштаб розсіювання її можливих значень навколо її центру, яким зазвичай є математичне сподівання.
Нехай X— випадкова величина, а М(Х) — її математичне сподівання.
Випадкову величину X- М(Х) називають відхиленням.
Математичне сподівання відхилення дорівнює нулю.
М[Х-М(Х)]=0. (1.9)
За властивостями математичного сподівання
М[Х- М(Х)]= М(Х) - М(М(Х)) = М(Х) - М(Х) = 0.
Дисперсією випадкової величини називають математичне сподівання квадрату відхилення.
D(X) = M{[X-M(X)]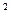 }
}
Дисперсії неперервної випадкової величини задається формулою:
D(X) = 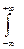 [x-M(X)]2-f(x)dx. (1.10)
[x-M(X)]2-f(x)dx. (1.10)
Дисперсія має такі властивості:
Дисперсія постійної величини С дорівнює нулю.
D(С) = 0.
Постійний множник виноситься за знак дисперсії в квадраті
D(C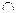 X)=C
X)=C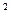 D(X)
D(X)
Дисперсія об'єднання (різниці) двох незалежних випадкових величин дорівнює сумі дисперсій цих величин.
D(X± Y) = D(X) + D(Y).
Дисперсія числа появи події А в п незалежних випробуваннях рівна добутку числа випробувань на ймовірності появи і непояви події А в одному випробуванні:
D(X) = npq.
Для оцінки розсіювання значень випадкової величини X навколо її середнього значення поряд з дисперсією використовують і інші числові характеристики. Однією з них є середнє квадратичне відхилення (у деяких посібниках його називають стандартним відхиленням).
Середнім квадратичним відхиленням випадкової величини X називають корінь квадратний із дисперсії:
σ(X)=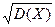 (1.11)
(1.11)
На практиці часто зустрічаються випадкові процеси, які описуються нормальним законом розподілу.
Числові характеристики часто використовуються для прийняття рішень в умовах ризику, коли всі можливі варіанти, що можуть виникнути в даній проблемі, є відомі і той, хто приймає рішення, має достатньо інформації, щоб вказати їх вірогідність.
Ці можливості можуть коливатись від суб'єктивних знань, які ґрунтуються на інтуїції і досвіді тих, хто приймає рішення до об'єктивних знань, що ґрунтуються на зібраних та проаналізованих даних, які відносяться до станів можливих варіантів.
Крім одномірних випадкових величин, трапляються випадкові величини, значення яких визначаються двома, трьома, ..., п числами, їх відповідно називають двовимірними, тривимірними, ..., п-вимірними.
Розглянемо спочатку двовимірну дискретну випадкову величину. Під законом розподілу такої величини будемо розуміти перелік можливих значень цієї величини, тобто пар чисел (хі ,yj) і їх ймовірностей p(xi,yj)
і їх ймовірностей p(xi,yj)
(і = 1,..., п), (j= 1, ..., m). Зазвичай, закон розподілу такої випадкової величини задається таблицею.
Припускається, що всі можливі комбінації подій {X = xі,Y = yj} утворюють повну групу подій. Знаючи закон розподілу двовимірної дискретної випадкової величини, можна знайти закони розподілу окремих її складових.
Для характеристики умовних законів розподілу можемо використати числові характеристики, що вже використовувалися раніше для одномірних випадкових величин.
Найбільш важливою з них є умовне математичне сподівання.