рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Вид работы: Лекции
- /
- Бесконечно большие функции и их связь с
Реферат Курсовая Конспект
Бесконечно большие функции и их связь с
Бесконечно большие функции и их связь с - Лекция, раздел Образование, Числовая последовательность Бесконечно Малыми. Определение. Преде...
бесконечно малыми.
Определение. Предел функции f(x) при х®а, где а- число, равен бесконечности, если для любого числа М>0 существует такое число D>0, что неравенство
ïf(x)ï>M
выполняется при всех х, удовлетворяющих условию
0 < ïx - aï < D
Записывается  .
.
Собственно, если в приведенном выше определении заменить условие ïf(x)ï>M на f(x)>M, то получим:

а если заменить на f(x)<M, то:

Графически приведенные выше случаи можно проиллюстрировать следующим образом:
 |
a x a x a x
Определение. Функция называется бесконечно большойпри х®а, где а – чосли или одна из величин ¥, +¥ или -¥, если 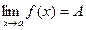 , где А – число или одна из величин ¥, +¥ или -¥.
, где А – число или одна из величин ¥, +¥ или -¥.
Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой.
Теорема. Если f(x)®0 при х®а (если х®¥ ) и не обращается в ноль, то

Сравнение бесконечно малых функций.
Пусть a(х), b(х) и g(х) – бесконечно малые функции при х ® а. Будем обозначать эти функции a, b и g соответственно. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.
Например, функция f(x) = x10 стремится к нулю быстрее, чем функция f(x) = x.
Определение. Если  , то функция a называется бесконечно малой более высокого порядка, чем функция b.
, то функция a называется бесконечно малой более высокого порядка, чем функция b.
Определение. Если  , то a и b называются бесконечно малыми одного порядка.
, то a и b называются бесконечно малыми одного порядка.
Определение. Если  то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.
то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.
Пример. Сравним бесконечно малые при х®0 функции f(x) = x10 и f(x) = x.

т.е. функция f(x) = x10 – бесконечно малая более высокого порядка, чем f(x) = x.
Определение. Бесконечно малая функция a называется бесконечно малой порядка kотносительно бесконечно малой функции b, если предел  конечен и отличен от нуля.
конечен и отличен от нуля.
Однако следует отметить, что не все бесконечно малые функции можно сравнивать между собой. Например, если отношение 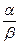 не имеет предела, то функции несравнимы.
не имеет предела, то функции несравнимы.
Пример. Если  , то при х®0
, то при х®0 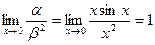 , т.е. функция a - бесконечно малая порядка 2 относительно функции b.
, т.е. функция a - бесконечно малая порядка 2 относительно функции b.
Пример. Если  , то при х®0
, то при х®0 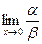 не существует, т.е. функция a и b несравнимы.
не существует, т.е. функция a и b несравнимы.
Свойства эквивалентных бесконечно малых.
1) a ~ a, 
2) Если a ~ b и b ~ g, то a ~ g, 
3) Если a ~ b, то b ~ a, 
4) Если a ~ a1 и b ~ b1 и 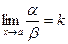 , то и
, то и  или
или  .
.
Следствие: а) если a ~ a1 и 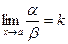 , то и
, то и 
б) если b ~ b1 и 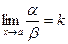 , то
, то 
Свойство 4 особенно важно на практике, т.к. оно фактически означает, что предел отношения бесконечно малых не меняется при замене их на эквивалентные бесконечно малые. Этот факт дает возможность при нахождении пределов заменять бесконечно малые на эквивалентные им функции, что может сильно упростить вычисление пределов.
Пример. Найти предел 
Так как tg5x ~ 5x и sin7x ~ 7x при х ® 0, то, заменив функции эквивалентными бесконечно малыми, получим:

Пример. Найти предел  .
.
Так как 1 – cosx = 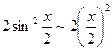 при х®0, то
при х®0, то  .
.
Пример. Найти предел 
Если a и b - бесконечно малые при х®а, причем b - бесконечно малая более высокого порядка, чем a, то g = a + b - бесконечно малая, эквивалентная a. Это можно доказать следующим равенством  .
.
Тогда говорят, что a - главная частьбесконечно малой функции g.
Пример. Функция х2 +х – бесконечно малая при х®0, х – главная часть этой функции. Чтобы показать это, запишем a = х2, b = х, тогда
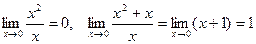 .
.
Некоторые замечательные пределы.
 , где P(x) = a0xn + a1xn-1 +…+an,
, где P(x) = a0xn + a1xn-1 +…+an,
Q(x) = b0xm + b1xm-1 +…+bm - многочлены.
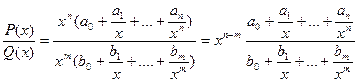


Итого: 

Первый замечательный предел. 

Второй замечательный предел. 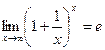
Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.
Кроме трех, изложенных выше, пределов можно записать следующие полезные на практике соотношения:


Пример. Найти предел.

Пример. Найти предел.
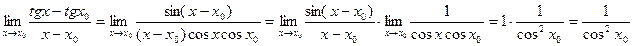
Пример. Найти предел.

Пример. Найти предел.

Пример. Найти предел.

Пример. Найти предел 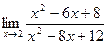 .
.
Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби.
x2 – 6x + 8 = 0; x2 – 8x + 12 = 0;
D = 36 – 32 = 4; D = 64 – 48 = 16;
x1 = (6 + 2)/2 = 4; x1 = (8 + 4)/2 = 6;
x2 = (6 – 2)/2 = 2 ; x2 = (8 – 4)/2 = 2;
Тогда 
Пример. Найти предел.
 домножим числитель и знаменатель дроби на сопряженное выражение:
домножим числитель и знаменатель дроби на сопряженное выражение:  =
=
= .
.
Пример. Найти предел.

Пример. Найти предел 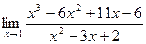 .
.
Разложим числитель и знаменатель на множители.
x2 – 3x + 2 = (x – 1)(x – 2)
x3 – 6x2 + 11x – 6 = (x – 1)(x – 2)(x – 3), т.к.
 x3 – 6x2 + 11x – 6 x - 1
x3 – 6x2 + 11x – 6 x - 1
x3 – x2 x2 – 5x + 6
- 5x2 + 11x
- 5x2 + 5x
6x - 6
6x - 6 0
x2 – 5x + 6 = (x – 2)(x – 3)
Тогда 
Пример. Найти предел.

 - не определен, т.к. при стремлении х к 2 имеют место различные односторонние пределы -∞ и +∞.
- не определен, т.к. при стремлении х к 2 имеют место различные односторонние пределы -∞ и +∞.
Непрерывность функции в точке.
Определение. Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точкех0, если предел функции и ее значение в этой точке равны, т.е.

Тот же факт можно записать иначе: 
Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.
Пример непрерывной функции:
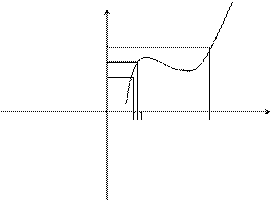 y
y
f(x0)+e
f(x0)
f(x0)-e
0 x0-D x0 x0+D x
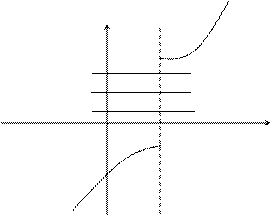 Пример разрывной функции:
Пример разрывной функции:
y
f(x0)+e
f(x0)
f(x0)-e
x0 x
Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа e>0 существует такое число D>0, что для любых х, удовлетворяющих условию

верно неравенство 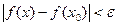 .
.
Определение. Функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной.
f(x) = f(x0) + a(x)
где a(х) – бесконечно малая при х®х0.
Свойства непрерывных функций.
1) Сумма, разность и произведение непрерывных в точке х0 функций – есть функция, непрерывная в точке х0.
2) Частное двух непрерывных функций  – есть непрерывная функция при условии, что g(x) не равна нулю в точке х0.
– есть непрерывная функция при условии, что g(x) не равна нулю в точке х0.
3) Суперпозиция непрерывных функций – есть непрерывная функция.
Это свойство может быть записано следующим образом:
Если u = f(x), v = g(x) – непрерывные функции в точке х = х0, то функция v = g(f(x)) – тоже непрерывнаяфункция в этой точке.
Справедливость приведенных выше свойств можно легко доказать, используя теоремы о пределах.
Непрерывность некоторых элементарных функций.
1) Функция f(x) = C, C = const – непрерывная функция на всей области определения.
2) Рациональная функция 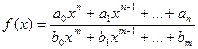 непрерывна для всех значений х, кроме тех, при которых знаменатель обращается в ноль. Таким образом, функция этого вида непрерывна на всей области определения.
непрерывна для всех значений х, кроме тех, при которых знаменатель обращается в ноль. Таким образом, функция этого вида непрерывна на всей области определения.
3) Тригонометрические функции sin и cos непрерывны на своей области определения.
Докажем свойство 3 для функции y = sinx.
Запишем приращение функции Dy = sin(x + Dx) – sinx, или после преобразования:

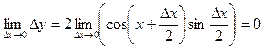
Действительно, имеется предел произведения двух функций  и
и  . При этом функция косинус – ограниченная функция при Dх®0
. При этом функция косинус – ограниченная функция при Dх®0  , а т.к.
, а т.к.
предел функции синус  , то она является бесконечно малой при Dх®0.
, то она является бесконечно малой при Dх®0.
Таким образом, имеется произведение ограниченной функции на бесконечно малую, следовательно это произведение, т.е. функция Dу – бесконечно малая. В соответствии с рассмотренными выше определениями, функция у = sinx – непрерывная функция для любого значения х = х0 из области определения, т.к. ее приращение в этой точке – бесконечно малая величина.
Точки разрыва и их классификация.
Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х0, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х0 является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.
Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.
Если односторонний предел (см. выше)  , то функция называется непрерывной справа.
, то функция называется непрерывной справа.
 |
х0
Если односторонний предел (см. выше)  , то функция называется непрерывной слева.
, то функция называется непрерывной слева.
 |
х0
Определение. Точка х0 называется точкой разрывафункции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.
Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее.
Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимойточкой разрыва, но подробнее об этом поговорим ниже.
Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Пример. Функция Дирихле (Дирихле Петер Густав(1805-1859) – немецкий математик, член- корреспондент Петербургской АН 1837г)
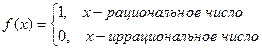
не является непрерывной в любой точке х0.
Пример. Функция f(x) =  имеет в точке х0 = 0 точку разрыва 2 – го рода, т.к.
имеет в точке х0 = 0 точку разрыва 2 – го рода, т.к.
 .
.


Пример. f(x) = 
Функция не определена в точке х = 0, но имеет в ней конечный предел  , т.е. в точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к. если доопределить функцию:
, т.е. в точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к. если доопределить функцию:
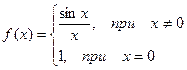
График этой функции:

Пример. f(x) =  =
=
 y
y
0 x
-1
Эта функция также обозначается sign(x) – знак х. В точке х = 0 функция не определена. Т.к. левый и правый пределы функции различны, то точка разрыва – 1 – го рода. Если доопределить функцию в точке х = 0, положив f(0) = 1, то функция будет непрерывна справа, если положить f(0) = -1, то функция будет непрерывной слева, если положить f(x) равное какому- либо числу, отличному от 1 или –1, то функция не будет непрерывна ни слева, ни справа, но во всех случаях тем не менее будет иметь в точке х = 0 разрыв 1 – го рода. В этом примере точка разрыва 1 – го рода не является устранимой.
Таким образом, для того, чтобы точка разрыва 1 – го рода была устранимой, необходимо, чтобы односторонние пределы справа и слева были конечны и равны, а функция была бы в этой точке не определена.
Непрерывность функции на интервале и на отрезке.
Определение. Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).
При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка или интервала.
Свойства функций, непрерывных на отрезке.
Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897)- немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие –M £ f(x) £ M.
Доказательство этого свойства основано на том, что функция, непрерывная в точке х0, ограничена в некоторой ее окрестности, а если разбивать отрезок [a, b] на бесконечное количество отрезков, которые “стягиваются” к точке х0, то образуется некоторая окрестность точки х0.
Свойство 2: Функция, непрерывная на отрезке [a, b], принимает на нем наибольшее и наименьшее значения.
Т.е. существуют такие значения х1 и х2, что f(x1) = m, f(x2) = M, причем
m £ f(x) £ M
Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например – f(x) = sinx).
Разность между наибольшим и наименьшим значением функции на отрезке называется колебаниемфункции на отрезке.
Свойство 3: (Вторая теорема Больцано – Коши). Функция, непрерывная на отрезке [a, b], принимает на этом отрезке все значения между двумя произвольными величинами.
Свойство 4: Если функция f(x) непрерывна в точке х = х0, то существует некоторая окрестность точки х0, в которой функция сохраняет знак.
Свойство 5: (Первая теорема Больцано (1781-1848) – Коши). Если функция f(x)- непрерывная на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f(x) = 0.
Т.е. если sign(f(a)) ¹ sign(f(b)), то $ х0: f(x0) = 0.
Определение. Функция f(x) называется равномерно непрерывной на отрезке [a, b], если для любого e>0 существует D>0 такое, что для любых точек х1Î[a,b] и x2Î[a,b] таких, что
ïх2 – х1ï< D
верно неравенство ïf(x2) – f(x1)ï < e
Отличие равномерной непрерывности от “обычной” в том, что для любого e существует свое D, не зависящее от х, а при “обычной” непрерывности D зависит от e и х.
Свойство 6: Теорема Кантора (Кантор Георг (1845-1918)- немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем.
(Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)
Пример. 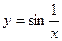

Функция 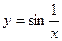 непрерывна на интервале (0, а), но не является на нем равномерно непрерывной, т.к. существует такое число D>0 такое, что существуют значения х1 и х2 такие, чтоïf(x1) – f(x2)ï>e, e - любое число при условии, что х1 и х2 близки к нулю.
непрерывна на интервале (0, а), но не является на нем равномерно непрерывной, т.к. существует такое число D>0 такое, что существуют значения х1 и х2 такие, чтоïf(x1) – f(x2)ï>e, e - любое число при условии, что х1 и х2 близки к нулю.
Свойство 7: Если функция f(x) определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция х = g(y) тоже однозначна, монотонна и непрерывна.
Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.
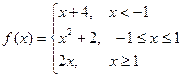


в точке х = -1 функция непрерывна в точке х = 1 точка разрыва 1 – го рода
 у
у
-4 -1 0 1 х
Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.

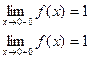

в точке х = 0 функция непрерывна в точке х = 1 точка разрыва 1 – го рода
 |
у
-p -p/2 0 1 x
Лекция № 12. Понятие функции одной переменной. График функции. Способы задания функций. Понятие сложной функции и обратной функции. Ограниченность, монотонность, четность и нечетность, периодичность функций.
Рассмотрим два множества 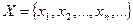 и
и  . Правило, позволяющее каждому элементу
. Правило, позволяющее каждому элементу  поставить в соответствие единственный элемент
поставить в соответствие единственный элемент  , называется функцией одной переменной
, называется функцией одной переменной  и обозначается символом
и обозначается символом 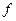 . При этом элементы
. При этом элементы  множества
множества 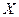 называют аргументами, а само множество
называют аргументами, а само множество 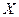 называют областью определения функции
называют областью определения функции 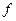 и обозначают символом
и обозначают символом  . Тот элемент
. Тот элемент  , который соответствует элементу
, который соответствует элементу  , называют образом элемента
, называют образом элемента  , или значением функции и обозначают символом
, или значением функции и обозначают символом  , а сам элемент
, а сам элемент  называют прообразом элемента
называют прообразом элемента  . Множество всех образов элементов множества
. Множество всех образов элементов множества 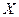 называют множеством значений функции
называют множеством значений функции 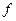 и обозначают символом
и обозначают символом  .
.
Графиком функции 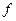 с областью определения
с областью определения 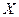 называют множество точек плоскости с координатами
называют множество точек плоскости с координатами 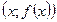 , где
, где  пробегает всю область определения
пробегает всю область определения 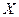 .
.
Основными способами задания функций являются аналитический, графический и табличный. Аналитическим способом называют задание функции 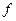 формулой вида
формулой вида 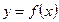 . Графический способ задания функции
. Графический способ задания функции 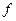 состоит в задании функции ее графиком. Если же функция
состоит в задании функции ее графиком. Если же функция 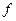 задана таблицей вида
задана таблицей вида
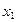
|  
| 
| … | 
|
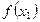
| 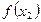
| 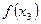
| … | 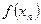
|
то говорят, что функция задана табличным способом.
Пусть имеем функцию 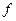 с областью определения
с областью определения 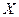 и множеством значений
и множеством значений  . Если любые два различные значения
. Если любые два различные значения  имеют различные образы, то появляется возможность установить обратное соответствие между множествами
имеют различные образы, то появляется возможность установить обратное соответствие между множествами  и
и 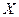 так, чтобы каждому значению
так, чтобы каждому значению  сопоставлялся единственный
сопоставлялся единственный  , тот самый, для которого рассматриваемый
, тот самый, для которого рассматриваемый  являлся образом
являлся образом  функции
функции 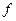 . Это обратное соответствие называют обратной функцией для функции
. Это обратное соответствие называют обратной функцией для функции 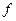 и обозначают символом
и обозначают символом  . Очевидно, что если функция
. Очевидно, что если функция 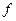 с областью определения
с областью определения 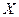 и множеством значений
и множеством значений  имеет обратную, то для функции
имеет обратную, то для функции  множество
множество  будет областью определения, а множество
будет областью определения, а множество 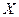 множеством значений.
множеством значений.
Рассмотрим теперь три множества 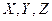 . Допустим, что каждому значению
. Допустим, что каждому значению  функция
функция 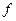 сопоставляет единственное значение
сопоставляет единственное значение  , а каждому значению
, а каждому значению  функция
функция  сопоставляет единственное значение
сопоставляет единственное значение  . Тогда с помощью функций
. Тогда с помощью функций 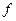 и
и  каждому значению
каждому значению  можно поставить в соответствие единственный элемент
можно поставить в соответствие единственный элемент 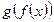 множества
множества  . Это соответствие называют сложной функцией (или суперпозицией) с областью определения
. Это соответствие называют сложной функцией (или суперпозицией) с областью определения 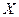 и обозначают символом
и обозначают символом 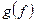 .
.
Функция 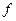 , определенная на множестве
, определенная на множестве 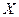 , называется ограниченной сверху (снизу) если множество значений этой функции ограничено сверху (снизу), т.е.
, называется ограниченной сверху (снизу) если множество значений этой функции ограничено сверху (снизу), т.е. 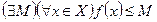
 .
.
Функция 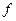 называется монотонно возрастающей (убывающей) на множестве
называется монотонно возрастающей (убывающей) на множестве 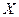 , если
, если 
 .
.
Монотонность функции 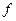 является достаточным условием существования обратной функции
является достаточным условием существования обратной функции  .
.
Множество 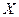 называют симметричным, если вместе с любым своим элементом
называют симметричным, если вместе с любым своим элементом  оно содержит и противоположный элемент
оно содержит и противоположный элемент  . Функция
. Функция  определенная на симметричном множестве
определенная на симметричном множестве 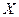 , называется четной (нечетной), если
, называется четной (нечетной), если 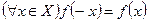
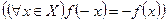 .
.
Функцию 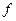 , определенную на множестве
, определенную на множестве 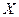 , называют периодической, если
, называют периодической, если  . Число
. Число 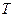 при этом называют периодом функции.
при этом называют периодом функции.
Нетрудно доказать, что если функция 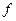 периодическая и
периодическая и 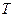 - ее период, то числа
- ее период, то числа  , где
, где 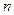 - натуральное число, также являются периодами функции
- натуральное число, также являются периодами функции 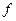 . Наименьший положительный период называют основным периодом.
. Наименьший положительный период называют основным периодом.
Лекция № 13 Основные элементарные функции: постоянная, степенная, показательная, логарифмическая, тригонометрические, обратные тригонометрические функции.
Функции  , где
, где 
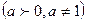 ,
, 
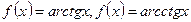 называют основными элементарными функциями. Элементарной называют функцию, аналитическое выражение которой содержит лишь конечное число арифметических операций и конечное число суперпозиций основных элементарных функций.
называют основными элементарными функциями. Элементарной называют функцию, аналитическое выражение которой содержит лишь конечное число арифметических операций и конечное число суперпозиций основных элементарных функций.
Лекция № 14 Числовая последовательность. Сходящиеся и расходящиеся последовательности. Основные теоремы о пределе последовательности.
Числовую функцию  , областью определения которой является множество натуральных чисел
, областью определения которой является множество натуральных чисел  , называют функцией натурального аргумента или числовой последовательностью. В общем виде числовую последовательность (или просто последовательность) обозначают символом
, называют функцией натурального аргумента или числовой последовательностью. В общем виде числовую последовательность (или просто последовательность) обозначают символом  или
или  .
.
Для последовательностей важны два способа задания :
1. Аналитический, т.е. с помощью формулы 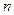 -го члена вида
-го члена вида  .
.
2. Рекуррентный: задают один или несколько первых членов последовательности и формулу, позволяющую определить любой член последовательности по известным предыдущим членам.
Числовые последовательности как функции могут быть ограниченными сверху (снизу), неограниченными, монотонными и немонотонными. Но не имеет смысла ставить вопрос о четности или нечетности последовательности, так как множество  не является симметричным.
не является симметричным.
Числовую последовательность  называют сходящейся к числу
называют сходящейся к числу 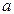 , если для любого числа
, если для любого числа  > 0 найдется номер N такой что при всех
> 0 найдется номер N такой что при всех 
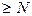 выполняется неравенство
выполняется неравенство  <
<  . Число
. Число 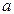 при этом называют пределом последовательности (
при этом называют пределом последовательности ( ) и обозначают символом
) и обозначают символом  . В символах математической логики определение того, что
. В символах математической логики определение того, что  запишется так:
запишется так:  .
.
Последовательность  называется расходящейся к плюс (минус) бесконечности, если для любого числа Е найдется такой номер N, что при всех
называется расходящейся к плюс (минус) бесконечности, если для любого числа Е найдется такой номер N, что при всех  выполняется неравенство
выполняется неравенство  . Обозначение :
. Обозначение : 
 .
.
К основным теоремам о пределе последовательности относят следующие теоремы.
Теорема 1. Если последовательность имеет предел, то он единственный.
Теорема 2. Всякая сходящаяся последовательность ограничена.
Теорема 3. Всякая монотонная ограниченная последовательность имеет предел.
Теорема 4. Если последовательность  сходится к числу
сходится к числу 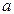 , а
, а
последовательность  сходится к числу
сходится к числу  и при этом
и при этом 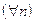
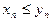 ,
,
то  .
.
Теорема 5. Пусть даны три последовательности  ,
, и
и такие, что
такие, что
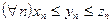 . Если
. Если  , то
, то 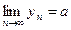 .
.
Последовательность  , где
, где  некоторое число, называют постоянной. Все ее члены равны
некоторое число, называют постоянной. Все ее члены равны  . Очевидно, что такая последовательность является ограниченной и сходящейся. Ее пределом является число
. Очевидно, что такая последовательность является ограниченной и сходящейся. Ее пределом является число  :
: 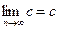 .
.
Лекция № 15 Бесконечно малые и бесконечно большие последовательности и их свойства. Неопределенности. Число е.
Определение 1. Последовательность  называют бесконечно малой,
называют бесконечно малой,
если 
 (т.е. если
(т.е. если 
Теорема 1. Чтобы последовательность  сходилась к числу
сходилась к числу 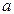 , необходимо и
, необходимо и
достаточно чтобы последовательность  была бесконечно
была бесконечно
малой.
Теорема 2. Сумма двух бесконечно малых последовательностей является
бесконечно малой последовательностью.
Замечание. Легко заметить, что эту теорему можно обобщить на любое конечное число слагаемых. Например, для доказательства, что сумма трех бесконечно малых последовательностей является бесконечно малой последовательностью, достаточно дважды применить теорему 2.
Теорема 3. Если  является бесконечно малой последовательностью, а
является бесконечно малой последовательностью, а  -
-
ограниченная последовательность, то  есть бесконечно малая
есть бесконечно малая
последовательность.
Следствие 1. Если  - бесконечно малая последовательность, а
- бесконечно малая последовательность, а  - некоторое
- некоторое
действительное число, то  является бесконечно малой
является бесконечно малой
последовательностью.
Следствие 2. Произведение конечного числа бесконечно малых
последовательностей является бесконечно малой
последовательностью.
Следствие 3. Если 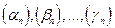 -
-  бесконечно малых последовательностей, а
бесконечно малых последовательностей, а
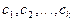 - действительные числа, то последовательность
- действительные числа, то последовательность
 является бесконечно малой.
является бесконечно малой.
Определение 2. Последовательность  называют бесконечно большой,
называют бесконечно большой,
если  , т.е. если
, т.е. если 
Теорема 4. Чтобы последовательность  была бесконечно большой,
была бесконечно большой,
необходимо и достаточно чтобы последовательность  , где
, где
 , была бесконечно малой.
, была бесконечно малой.
Теорема 5. Если последовательности  и
и  сходятся к числам
сходятся к числам 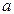 и
и 
соответственно, то
1) последовательность  сходится к числу
сходится к числу  ;
;
2) последовательность  сходится к числу
сходится к числу  ;
;
3) последовательность  сходится к числу
сходится к числу  .
.
Теорема 6. Если последовательность  сходится к числу
сходится к числу 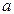 ;
;
последовательность  сходится к числу
сходится к числу  , то
, то
последовательность  сходится к числу
сходится к числу  .
.
Неопределенностями называют пределы некоторых последовательностей, которые в зависимости от конструкции последовательностей могут принимать различные значения или не существовать. К неопределенностям относят 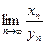 , если
, если  (неопределенность типа
(неопределенность типа  );
); 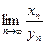 , если
, если  (неопределенность типа
(неопределенность типа 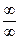 );
); 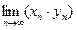 , если
, если  (неопределенность типа
(неопределенность типа  );
);  , если
, если 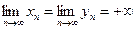 или
или  (неопределенность типа
(неопределенность типа  );
); 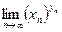 , где
, где 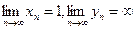 (неопределенность типа
(неопределенность типа 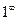 );
); 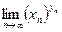 , где
, где 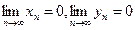 (неопределенность типа
(неопределенность типа  );
); 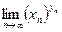 , где
, где  (неопределенность типа
(неопределенность типа  )
)
Последовательность 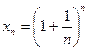 ограничена сверху и монотонно возрастает, а, следовательно, сходится. Предел этой последовательности принято обозначать буквой
ограничена сверху и монотонно возрастает, а, следовательно, сходится. Предел этой последовательности принято обозначать буквой  .
.
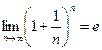
Число  - иррациональное; его можно представить в виде бесконечной непериодической десятичной дроби:
- иррациональное; его можно представить в виде бесконечной непериодической десятичной дроби:  = 2,718281828459045...
= 2,718281828459045...
Это число часто принимают за основание степени, а показательную функцию  называют экспонентой. Логарифм числа
называют экспонентой. Логарифм числа  по основанию
по основанию 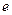 называют натуральным логарифмом и обозначают
называют натуральным логарифмом и обозначают 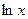 .
.
Лекция № 16 Предел функции в точке и на бесконечности. Основные теоремы о пределе функции. Односторонние пределы. Непрерывность функции. Первый и второй замечательные пределы.
Число 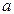 называют пределом функции
называют пределом функции  при
при  (на плюс бесконечности), если для любого
(на плюс бесконечности), если для любого 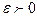 найдется число
найдется число  такое, что при всех
такое, что при всех 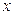 , удовлетворяющих неравенству
, удовлетворяющих неравенству 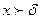 , выполняется неравенство
, выполняется неравенство  . Обозначение :
. Обозначение : 
В символах математической логики тот факт, что  выглядит так
выглядит так 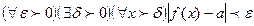 .
.
Число 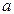 называют пределом функции
называют пределом функции  при
при  (на минус бесконечности), если
(на минус бесконечности), если  . Обозначение :
. Обозначение : 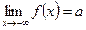 .
.
Число 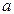 называют пределом функции
называют пределом функции  в точке
в точке  , если
, если 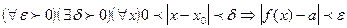 . Обозначение :
. Обозначение :  .
.
Это определение называют определением предела функции в точке на языке  , или определением предела по Коши в честь знаменитого французского математика, сформулировавшего его.
, или определением предела по Коши в честь знаменитого французского математика, сформулировавшего его.
Существует другое определение предела функции в точке, сформулированное немецким математиком Гейне - определение на языке последовательностей.
Число 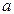 называют пределом функции
называют пределом функции  в точке
в точке  , если для любой последовательности
, если для любой последовательности  , сходящейся к
, сходящейся к  ,
,
– Конец работы –
Эта тема принадлежит разделу:
Числовая последовательность
Числовая последовательность Определение Если каждому натуральному числу n поставлено в соответствие число хn то говорят что... Лекция Некоторые пределы связанные с показательной и логарифмической... Теорема...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Бесконечно большие функции и их связь с
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов