Пример 1. Определить являются ли высказываниями следующие предложения, и установить истинность или ложность имеющихся высказываний
Практическое занятие № 2. Математические основы информатики.
Алгебра высказываний. Операции над множествами. Графы и
Способы задания графов. Релейно-контактные схемы
Основное понятие алгебры логики – высказывание. Основные понятия любой отрасли науки не могут быть определены строго формально, а лишь поясняются. Логическое значение высказывания “истина” (“ложь”) чаще всего обозначаются цифрой 1 (0). Все высказывания можно разделить на простые и составные или сложные. Логическое значение любого высказывания легко может быть установлено с помощью таблиц истинности основных логических операций.
Пример 1. Определить являются ли высказываниями следующие предложения, и установить истинность или ложность имеющихся высказываний:
1. число 15 не делится на 3;
2. летайте самолётами Аэрофлота!
3. есть ли жизнь на Марсе?
4. в Петербурге более 4-х миллионов жителей;
5. все действительные числа удовлетворяют коммутативному закону.
Из приведённых пяти предложений второе и третье не являются высказываниями, т. к. высказыванием может быть лишь повествовательное предложение. Первое высказывание ложно, четвертое и пятое – истинны.
Пример 2. Составить таблицу истинности для формулы 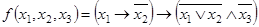 .
.
Применение таблицы истинности – самый простой способ исследования булевой функции. Каждая таблица для функции 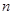 переменных содержит
переменных содержит 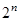 строк, поэтому таблицы истинности удобно применять, если функция содержит не более 3-4-х переменных. В нашем случае
строк, поэтому таблицы истинности удобно применять, если функция содержит не более 3-4-х переменных. В нашем случае
Таблица 1.19
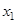
| 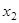
| 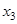
| 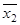
| 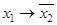
| 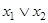
| 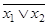
| 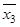
| 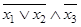
| 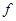
|
По табл. 1.19 видно, что формула 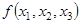 - выполнима, т. к. принимает значения 0 и 1 при разных наборах переменных
- выполнима, т. к. принимает значения 0 и 1 при разных наборах переменных 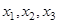 .
.
Пример 3. Доказать, что если формулы 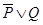 и
и 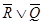 тождественно истинны, то формула
тождественно истинны, то формула 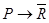 также тождественно истинна.
также тождественно истинна.
Предположим обратное, пусть 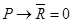 . Тогда из таблицы 1.16
. Тогда из таблицы 1.16 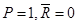 , т. е.
, т. е. 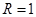 . Следовательно,
. Следовательно, 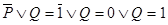 и
и 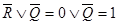 , т. е.
, т. е. 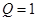 и
и 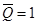 одновременно, что невозможно. Таким образом, наше предположение неверно и
одновременно, что невозможно. Таким образом, наше предположение неверно и 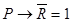 .
.
Пример 4. Булевы функции, представленные по формулам (1.13.4) и (1.13.5), находятся в виде совершенных дизъюнктивной и конъюнктивной нормальных форм. К такому виду любую булеву функцию можно привести путём эквивалентных преобразований с использованием формул (1.13.1)-(1.13.3). Однако самый простой, но не самый удобный способ – использование таблицы истинности.
По структуре формулы (1.13.4) ясно, что в её правой части стоят логические слагаемые, каждое из которых состоит из логического произведения всех переменных исходной формулы или их отрицаний, причём только из тех строк таблицы истинности, в которых сама функция равна единице.
Поэтому, чтобы получить совершенную дизъюнктивную нормальную форму булевой функции 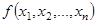 , необходимо записать в виде дизъюнкции все выражения вида
, необходимо записать в виде дизъюнкции все выражения вида 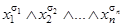 только в тех строках таблицы истинности, где
только в тех строках таблицы истинности, где 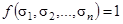 .
.
Рассмотрим в качестве примера функцию 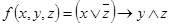 и её таблицу истинности 1.20.
и её таблицу истинности 1.20.
Таблица 1.20
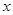
| 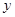
| 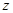
| 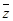
| 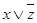
| 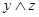
| 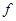
| 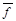
|
Тогда 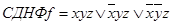 . Форму (1.13.5) удобнее получать не напрямую, а по формуле
. Форму (1.13.5) удобнее получать не напрямую, а по формуле 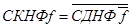 . В нашем случае
. В нашем случае 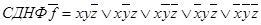 и
и 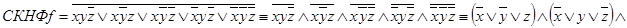
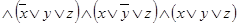 .
.
Алгебра логики и теория множеств являются двумя интерпретациями (моделями) одной общей теории, называемой алгеброй Буля*. Поэтому все понятия алгебры логики и теории множеств очень похожи.
 Пример 5. Доказать равенство
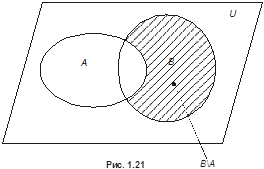
Пример 5. Доказать равенство 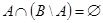 . Проще всего это сделать с помощью диаграмм Эйлера – Венна (см. рис. 1.21). Видно, что множества
. Проще всего это сделать с помощью диаграмм Эйлера – Венна (см. рис. 1.21). Видно, что множества 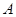 и
и 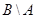 непересекающиеся, т. е. не имеют общих элементов. То же самое можно получить чисто формально:
непересекающиеся, т. е. не имеют общих элементов. То же самое можно получить чисто формально: 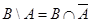 (см. рис. 1.21),
(см. рис. 1.21), 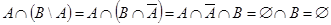 .
.
Пример 6. Пусть 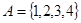 ,
, 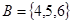 . Найти
. Найти 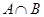 ,
, 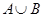 ,
, 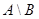 ,
, 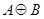 ,
, 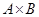 ,
, 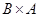 .
.
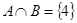 ,
, 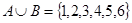 ,
, 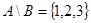 ,
, 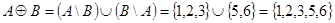 ,
, 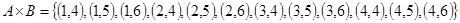 ,
, 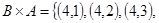
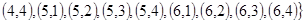 , очевидно
, очевидно 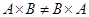 .
.
Пример 7. Дано бинарное отношение 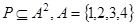 , изображённое на рис. 1. 22. Определить является ли оно рефлексивным, иррефлексивным, симметричным, антисимметричным, транзитивным?
, изображённое на рис. 1. 22. Определить является ли оно рефлексивным, иррефлексивным, симметричным, антисимметричным, транзитивным?
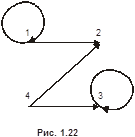 Матрица этого отношения имеет вид
Матрица этого отношения имеет вид 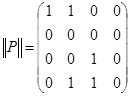 . Отношение
. Отношение 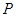 не рефлексивно, т. к. на главной диагонали его матрицы имеется два нуля; это отношение не иррефлексивно, т. к.
не рефлексивно, т. к. на главной диагонали его матрицы имеется два нуля; это отношение не иррефлексивно, т. к. 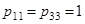 . Матрица
. Матрица 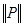 не симметрична, тогда не симметрично и отношение
не симметрична, тогда не симметрично и отношение 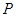 ; для симметричных отношений справедливо
; для симметричных отношений справедливо 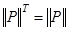 , что, очевидно, не выполняется в данном случае.
, что, очевидно, не выполняется в данном случае. 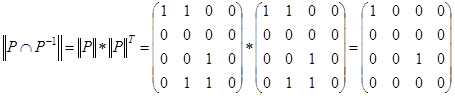 . Отношение
. Отношение 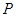 антисимметрично, т. к. все элементы, стоящие вне главной диагонали матрицы
антисимметрично, т. к. все элементы, стоящие вне главной диагонали матрицы 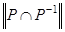 , равны нулю.
, равны нулю.
Транзитивность проще проверить по определению, используя элементы этого отношения: 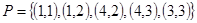 . По определению отношение
. По определению отношение 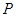 транзитивно, если из
транзитивно, если из 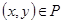 и
и 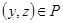 следует, что
следует, что 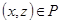 . В нашем случае
. В нашем случае 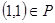 ,
, 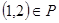 , но и
, но и 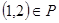 ;
; 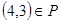 ,
, 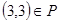 , но и
, но и 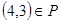 , т. е.
, т. е. 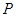 транзитивно.
транзитивно.
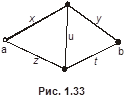
Пример 8. Для графов, изображённых на рис. 1.23, составить матрицу смежности вершин и инциденций.
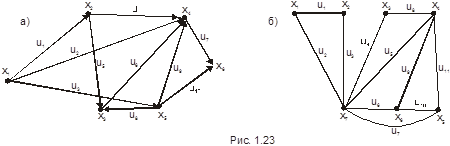
а) Дан ориентированный граф. Тогда
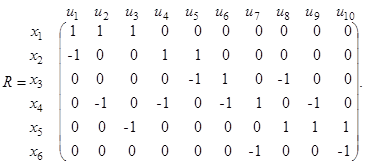
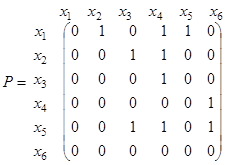
и
б) Этот граф неориентированный, поэтому матрица смежности вершин будет симметрической, а матрица инциденций – бинарной.
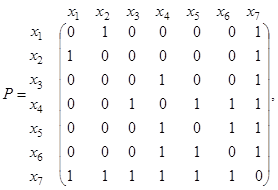
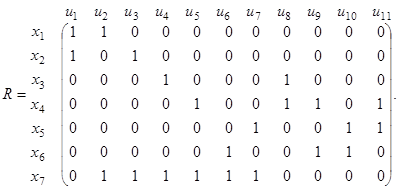
Пример 9. По данной матрице смежности вершин 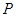 и инциденций
и инциденций 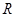 нарисовать соответствующий граф.
нарисовать соответствующий граф.
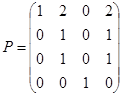 ,
, 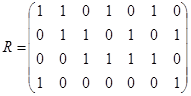 .
.
 По первой матрице
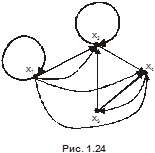
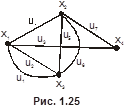
По первой матрице 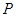 может быть построен ориентированный мульти- и псевдограф, изображённый на рис. 1.24. Следует помнить, что рисунок графа может быть и иным по расположению вершин и форме дуг, важно лишь количество вершин и дуг и порядок их инцидентности. Так как матрица
может быть построен ориентированный мульти- и псевдограф, изображённый на рис. 1.24. Следует помнить, что рисунок графа может быть и иным по расположению вершин и форме дуг, важно лишь количество вершин и дуг и порядок их инцидентности. Так как матрица 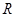 бинарна, то ей соответствующий граф будет неориентированным. Он изображён на рис. 1.25.
бинарна, то ей соответствующий граф будет неориентированным. Он изображён на рис. 1.25.
Пример 10. Найти эксцентриситет вершин, радиус и диаметр графа, изображённого на рис. 1.25.
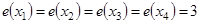 ,
, 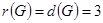 . Все вершины центральные и периферийные. Диаметральные цепи:
. Все вершины центральные и периферийные. Диаметральные цепи:
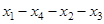
 ,
, 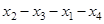
 ,
, 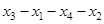
 ,
,
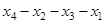 ,
, 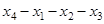 и т. п.
и т. п.
Пример 11. Реализовать релейно-контактными схемами функции: а) 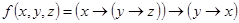 ;
;
б) 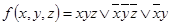 .
.
Поскольку релейно-контактные схемы реализуются на основе элементарных конъюнкции и дизъюнкции, то при необходимости следует упростить формулу по правилам (1.13.1)-(1.13.3).
а) 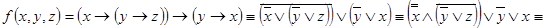
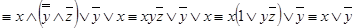 . Тогда релейно-контактная схема имеет вид, изображённый на рис. 1.26 а).
. Тогда релейно-контактная схема имеет вид, изображённый на рис. 1.26 а).
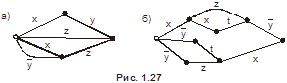
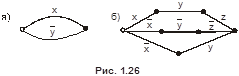
б) В этом случае формулу упрощать не требуется. Релейно-контактная схема этой формулы изображена на рис. 1.26 б).
Пример 12. Найти функции, реализуемые релейно-контактными схемами, изображёнными на рис. 1.27.
а) 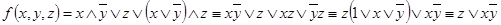 ;
;
б) 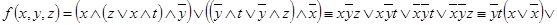
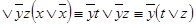 .
.
1.14.1. Обозначить элементарные высказывания буквами и записать следующие высказывания с помощью символов алгебры логики:
а) 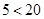 или
или 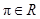 ;
;
б) если число 512 делится на 2 и 8, то оно делится на 16;
в) тает лёд и 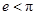 .
.
1.14.2. Пусть высказывание 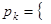 мишень поражена
мишень поражена 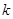 -м выстрелом
-м выстрелом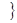 ,
, 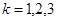 . Что означают следующие высказывания:
. Что означают следующие высказывания:
а) 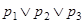 ;
;
б) 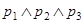 ;
;
в) 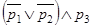 ?
?
1.14.3. Составить таблицы истинности для формул:
а) 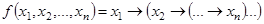 ;
;
б) 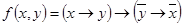 ;
;
в) 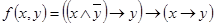 .
.
1.14.4. По таблице истинности получить СДНФ и СКНФ для формул:
а) 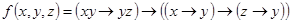 ;
;
б) 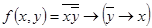 ;
;
в) 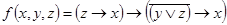 .
.
1.14.5. Доказать следующие тождества:
а) 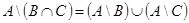 ;
;
б) 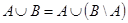 ;
;
в) 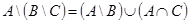 .
.
1.14.6. Определить в каком отношении (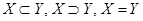 ) находятся множества
) находятся множества 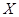 и
и 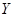 , если:
, если:
а) 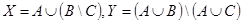 ;
;
б) 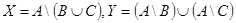 ;
;
в) 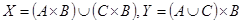 .
.
1.14.7. По данной матрице смежности вершин 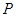 или инциденций
или инциденций 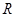 построить соответствующий граф:
построить соответствующий граф:
а) 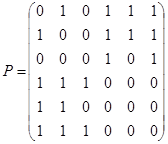 ; б)
; б) 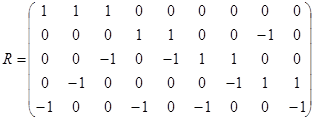 ;
;
в) 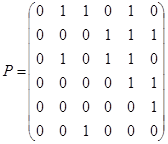 ; г)
; г) 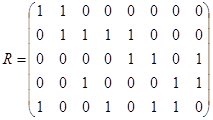 .
.
1.14.8. Для графов, изображённых на рис. 1.28, составить матрицы смежности вершин и инциденций:

1.14.9. Построить 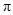 -схемы для формул:
-схемы для формул:
а) 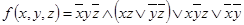 ;
;
б) 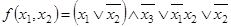 ;
;
в) 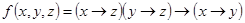 .
.
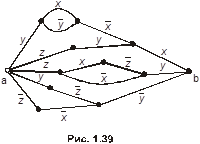
1.14.10. Найти функции, реализуемые контактными схемами, изображёнными на рис. 1.29.
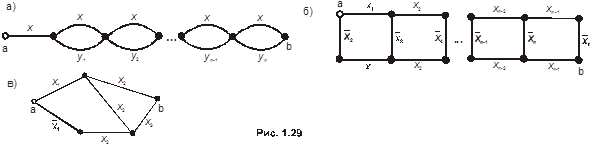
1.14.11. Варианты расчётно-графической работы.
Задание к расчётно-графической работе.
1. По таблице истинности найти СДНФ формулы алгебры логики.
2. Доказать равенство.
3. По данной матрице смежности вершин 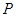 или инциденций
или инциденций 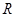 построить граф и найти его метрические характеристики (эксцентриситеты вершин, радиус и диаметр графа).
построить граф и найти его метрические характеристики (эксцентриситеты вершин, радиус и диаметр графа).
4. Восстановить булеву функцию по данной релейно-контактной схеме ( см. рис. 1.30-1.40) или построить релейно-контактную схему по данной функции.
Вариант 1
1. 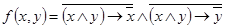 ;
;
2. 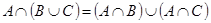 ;
;
3. 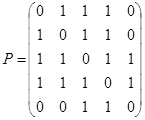 ;
;
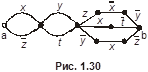
4.
Вариант 2
1. 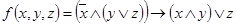 ;
;
2. 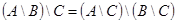 ;
;
3. 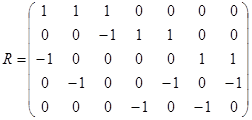 ;
;
4. 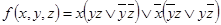 .
.
Вариант 3
1. 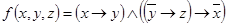 ;
;
2. 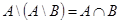 ;
;
3. 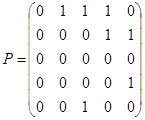 ;
;
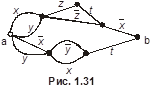
4.
Вариант 4
1. 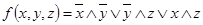 ;
;
2. 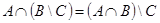 ;
;
3. 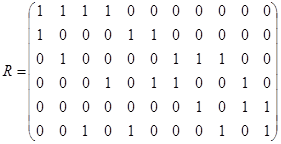 ;
;
4. 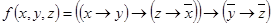 .
.
Вариант 5
1. 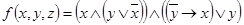 ;
;
2.  ;
;
3. 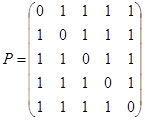 ;
;
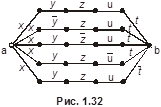
4.
Вариант 6
1. 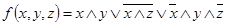 ;
;
2. 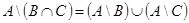 ;
;
3. 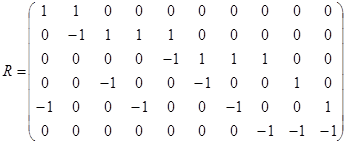 ;
;
4. 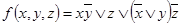 .
.
Вариант 7
1. 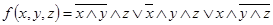 ;
;
2. 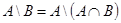 ;
;
3. 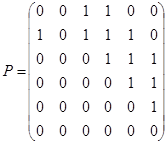 ;
;
4.
Вариант 8
1. 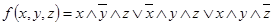 ;
;
2. 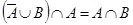 ;
;
3. 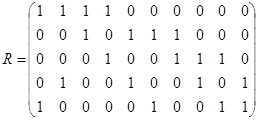 ;
;
4. 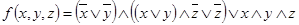 .
.
Вариант 9
1. 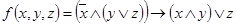 ;
;
2. 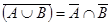 ;
;
3. 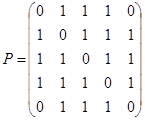 ;
;
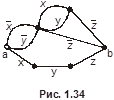
4.
Вариант 10
1. 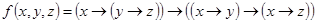 ;
;
2. 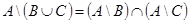 ;
;
3. 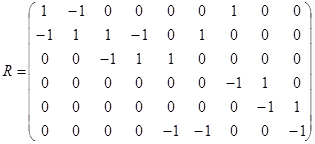 ;
;
4. 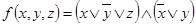 .
.
Вариант 11
1. 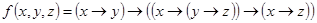 ;
;
2. 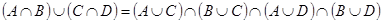 ;
;
3. 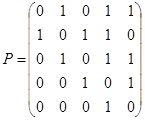 ;
;
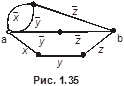
4.
Вариант 12
1. 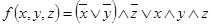 ;
;
2. 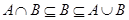 ;
;
3. 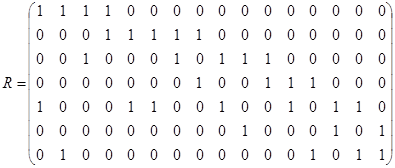 ;
;
4. 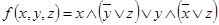 .
.
Вариант 13
1. 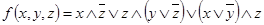 ;
;
2. 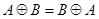 ;
;
3. 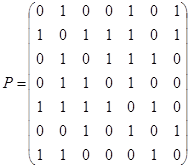 ;
;
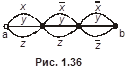
4.
Вариант 14
1. 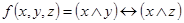 ;
;
2. 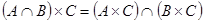 ;
;
3. 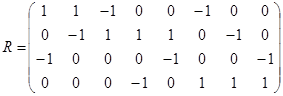 ;
;
4. 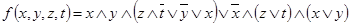 .
.
Вариант 15
1. 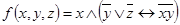 ;
;
2. 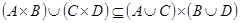 ;
;
3. 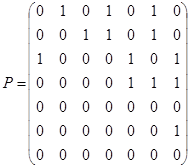 ;
;
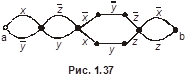
4.
Вариант 16
1. 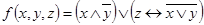 ;
;
2. 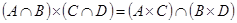 ;
;
3. 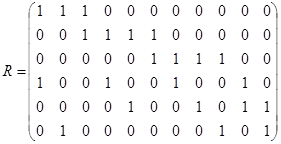 ;
;
4. 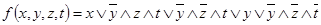 .
.
Вариант 17
1. 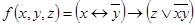 ;
;
2. 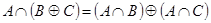 ;
;
3. 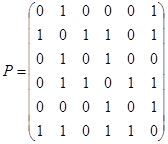 ;
;

4.
Вариант 18
1. 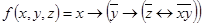 ;
;
2. 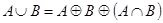 ;
;
3. 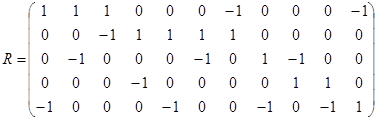 ;
;
4. 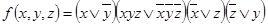 .
.
Вариант 19
1. 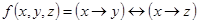 ;
;
2. 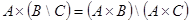 ;
;
3. 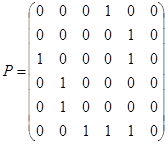 ;
;
4.
Вариант 20
1. 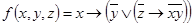 ;
;
2. 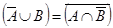 ;
;
3. 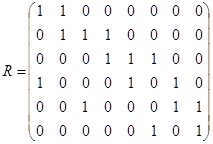 ;
;
4. 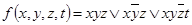 .
.
Вариант 21
1. 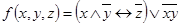 ;
;
2. 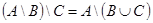 ;
;
3. 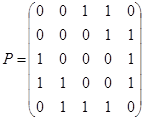 ;
;
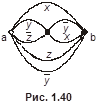
4.
Вариант 22
1. 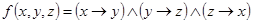 ;
;
2. 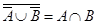 ;
;
3. 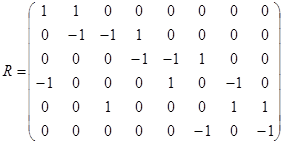 ;
;
4. 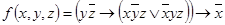 .
.
Вариант 23
1. 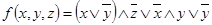 ;
;
2. 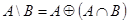 ;
;
3. 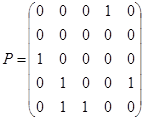 ;
;

4.
Вариант 24
1. 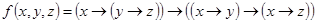 ;
;
2. 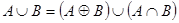 ;
;
3. 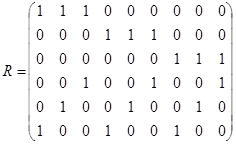 ;
;
4. 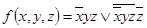 .
.
Вариант 25
1. 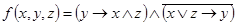 ;
;
2. 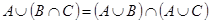 ;
;
3. 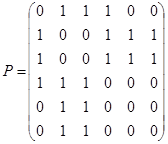 ;
;
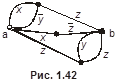
4.
Вариант 26
1. 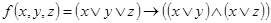 ;
;
2. 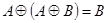 ;
;
3. 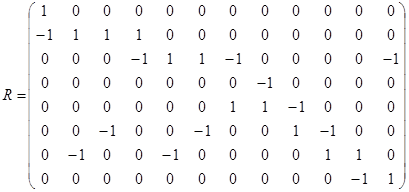 ;
;
4. 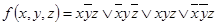 .
.
Вариант 27
1. 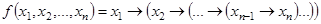 ;
;
2. 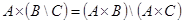 ;
;
3. 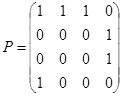 ;
;
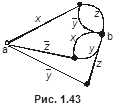
4.
Вариант 28
1. 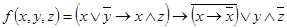 ;
;
2. 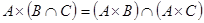 ;
;
3. 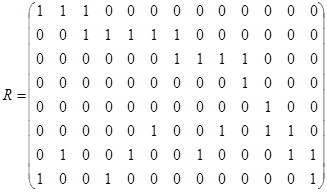 ;
;
4. 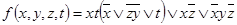 .
.
Вариант 29
1. 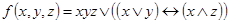 ;
;
2. если 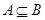 , то
, то 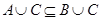 ;
;
3.  ;
;
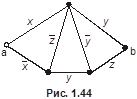
4.
Вариант 30
1. 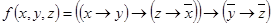 ;
;
2. если 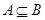 и
и 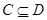 , то
, то 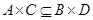 ;
;
3. 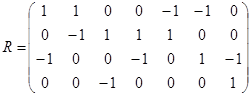 ;
;
4. 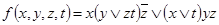 .
.
* Джордж Буль (1815-1864) – английский математик и логик.