рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Определение, примеры и простейшие свойства линейных пространств
Реферат Курсовая Конспект
Определение, примеры и простейшие свойства линейных пространств
Определение, примеры и простейшие свойства линейных пространств - раздел Образование, 1. Определение, Примеры И Простейшие Свойства Линейных Пространств...
1. Определение, примеры и простейшие свойства линейных пространств
Опр.1.1. Пусть P- поле. Непустое множество V называется линейным пространством (либо векторным пространством) над P (элементы V будем называть векторами, элементы P - скалярами), когда:
0) На V задана бинарная алгебраическая операция, которая называется сложением, или суммой, (то есть, "  ,
, ÎV указанный вектор
ÎV указанный вектор  +
+ ÎV), которая удовлетворяет условиям:
ÎV), которая удовлетворяет условиям:
1) " ,
, ,
,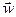 ÎV (
ÎV ( +
+ )+
)+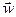 =
=  +(
+( +
+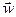 ); 2) $
); 2) $  ÎV, что "
ÎV, что "  ÎV
ÎV  +
+ =
= +
+ =
= ;
;
3) "  ÎV $ (-
ÎV $ (- ) ÎV такой, что
) ÎV такой, что  +(-
+(- )= (-
)= (- )+
)+ =
= ; 4) "
; 4) "  ,
, ÎV
ÎV  +
+  =
= +
+ ;
;
0’) Задана операция внешнего умножения скаляров (элементов из Р) на векторы (элементы из V) (то есть, что "lÎP, " ÎV, указанный вектор l
ÎV, указанный вектор l ÎV);
ÎV);
5) "l, m ÎP " ÎV (l×m)
ÎV (l×m) =l(m
=l(m ); 6) "l, m ÎP "
); 6) "l, m ÎP " ÎV (l+m)
ÎV (l+m) =l
=l +m
+m ;
;
7) "lÎP " ,
, ÎV l(
ÎV l( +
+ )=l
)=l +l
+l ; 8) "
; 8) " ÎV 1
ÎV 1 =
= .
.
Опр.1.2. Когда P=R, тогда V называется вещественным линейным пространством. Когда P=C, тогда V называется комплексным линейным пространством.
Примеры 1.3.
1.3.1. V2 - множество векторов плоскости с обычными операциями сложения и умножения вектора на число – действительное линейное пространство.
1.3.2. V3 - множество векторов в пространстве - действительное линейное пространство.
1.3.3. V={ } и "P "lÎP l
} и "P "lÎP l =
= ;
;  +
+ =
= - нулевое пространство.
- нулевое пространство.
1.3.4. "P; Mat(m´n; P) - линейное пространство над P.
1.3.5. "P; Mat(n´1; P)=Pⁿ - столбцы длины n, Pⁿ- арифметическое пространство.
1.3.6. "P, P[x] - множество всех полиномов из коэффициентами из Р.
1.3.7. "P, Pn[x] - множество всех полиномов из коэффициентами из Р, степени которых не большие за n.
1.3.8. C[a; b] – множество непрерывных на [a; b] функций. – Действительно линейное пространство. 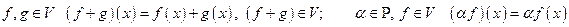
Св-во 1.4. Если V – линейное пространство, то <V,+> - коммутативная аддитивная группа. Из 1.4 и св-в групп следуют св-ва 1.5–1.7
Св-во 1.5.  в V единственный.
в V единственный.
Св-во 1.6. "  ÎV, противоположный вектор (-
ÎV, противоположный вектор (- ) единственный.
) единственный.
Св-во 1.7. " ,
, ÎV уравнение
ÎV уравнение  +x=
+x= имеет единственное решение x=(-
имеет единственное решение x=(- )+
)+  ..
..
Нулевой и противоположный векторы линейного пространства
Св-во 1.8. " ÎV 0=. Доказательство. (0+0)=0, 0+0=0, 0=. ■ Св-во 1.9. (-1) = – . Доказательство. 1+(-1)=0, (1+(-1)) =0, 1+(-1) =0, +(-1)… Св-во 1.10. "lÎP l=. Доказательство. По определению 1.1.2 +=, значит, l(+)=l, откуда по определению 1.1.7…Линейно зависимые системы векторов. Критерий линейной зависимости
Опр.2.2. Подпоследовательность ,,…,(2) последовательности (1), где 1£i1<i2<…<ik£nназывается подсистемой системы векторов (1). … Опр.2.3. Пусть дана система и последовательность l1, l2, …, ln (3) скаляров… Опр.2.4. Линейная комбинация (3) называется тривиальной, когда все ее коэффициенты равные нолю.Пример 2.8.
2.8.1. В V2 произвольная система из 2-х неколлинеарных векторов линейно независимые.
2.8.2. В V3 произвольная система из 3-х некомпланарных векторов линейно независимые.
2.8.3. В C[a; b] система векторов 1, sin²x, cos²x - линейно зависимые, так как (-1)×1+1×sin²x+1×cos²x=0.
2.8.4. В Pⁿ система векторов 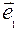 =
= ,
, 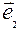 =
= 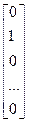 , … ,
, … , 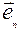 =
=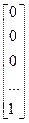 - линейно независимая.
- линейно независимая.
Св-во 2.9. Когда система векторов удерживает  , тогда она линейно зависимая.
, тогда она линейно зависимая.
Доказательство. 1 + 0
+ 0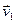 + … +0
+ … +0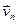 =
= .■
.■
Св-во 2.10. Когда система векторов удерживает линейно зависимую подсистему, тогда она линейно зависимая.
Доказательство. Без потери общности можно считать, что первые s векторов системы 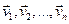 образовывают линейно зависимую подсистему l1
образовывают линейно зависимую подсистему l1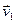 +…+ls
+…+ls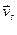 =
= , где не все lі=0. Из этого равенства очевидно, что l1
, где не все lі=0. Из этого равенства очевидно, что l1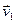 +…+ls
+…+ls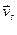 + 0
+ 0 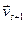 + … +0
+ … +0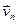 =
= , где не все коэффициенты равные нолю, значиться, система
, где не все коэффициенты равные нолю, значиться, система 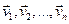 линейно зависимая. ■
линейно зависимая. ■
Вывод 2.11. Когда система векторов линейно независимая, тогда произвольная ее подсистема линейно независимая. Доказательство. Следует из 2.10 доказательствам от противного■
Опр.2.12. Будем говорить, что  линейно выражается через (1), $ l1, l2,…, lnÎR такие, что
линейно выражается через (1), $ l1, l2,…, lnÎR такие, что  =l1
=l1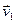 +l2
+l2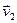 +…+ln
+…+ln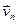 .
.
Св-во 2.13. Пусть  . Система
. Система 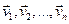 линейно зависимая тогда и только тогда, когда один из ее векторов линейно выражается через остальные векторы этой системы.
линейно зависимая тогда и только тогда, когда один из ее векторов линейно выражается через остальные векторы этой системы.
Доказательство. 1) 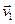 - линейно выражается через
- линейно выражается через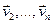 ,
,  .
.  линейно зависимая система
линейно зависимая система 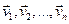 . 2) Наоборот. Пусть
. 2) Наоборот. Пусть 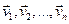 - линейно зависима.
- линейно зависима.  не все коэффициента равны нулю. Пусть
не все коэффициента равны нулю. Пусть  .
. 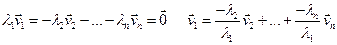 значит
значит 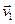 - линейно выражается через остальные. ■
- линейно выражается через остальные. ■
Выражение одной системы векторов через другую
Св-во 3.2. Произвольная подсистема системы векторов выражается через систему. Доказательство. = 0+…+1+…+0.■ Св-во 3.3. Когда система (1) линейно выражается через (2), а (2) линейно выражается через , ,…, (3) тогда (1) линейно…Основная теорема о линейной независимости
Т.3.11. (основная теорема о линейной независимости) Когда линейно независимая система (1) выражается через систему (2), тогда kL,т.е. в ней не может… Вывод 3.12. Когда система (1) линейно выражается через (2) и >, тогда (1) -… Вывод 3.13. Средь линейных комбинаций векторов из (2) не более линейно независимых.Подпространства. Определение, примеры, критерий подпространства
Опр. 7.1. Пусть V линейное пространство над полем Р. Непустое подмножество U Vназывают подпространством пространства V, когда U является линейным пространством относительно операций, какие указанный в V.
Vназывают подпространством пространства V, когда U является линейным пространством относительно операций, какие указанный в V.
Теорема.7.2.(Критерий подпространства). V линейное пространство над Р. Подмножество U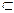 Vявляется подпространством в V тогда и только тогда, когда выполняются 3 условия: 1) U≠Ø; 2) Для каждых
Vявляется подпространством в V тогда и только тогда, когда выполняются 3 условия: 1) U≠Ø; 2) Для каждых 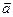 и
и 
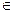 U
U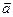 +
+
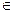 U;3) Для произвольного λ
U;3) Для произвольного λ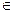 Р и для произвольного
Р и для произвольного 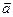
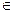 Uλ
Uλ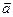
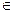 U. Доказательство. Когда U линейное подпространство, тогда 1), 2) и 3) очевидно выполняются. Пусть выполняются свойства 1), 2), 3). Тогда U≠Ø.
U. Доказательство. Когда U линейное подпространство, тогда 1), 2) и 3) очевидно выполняются. Пусть выполняются свойства 1), 2), 3). Тогда U≠Ø.
1.1.0 следует из 2). 1.1.1 выполняется, так как выполняется для произвольных элементов из V.
1.1.2 0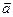 =
= , значиться по 1.8
, значиться по 1.8 
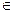 U. 1.1.3 По 1.9 (-1)
U. 1.1.3 По 1.9 (-1)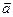 = -
= -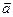 , значит по 3) -
, значит по 3) -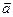
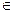 U.
U.
1.1.4 выполняется, так как выполняется для произвольных элементов из V. 1.1.0` следует из 3).
1.1.5-1.1.8 выполняются, так как выполняются для произвольных элементов из V и из Р.■
Эти свойства: 1) " ,
, ,
,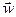 ÎV (
ÎV ( +
+ )+
)+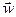 =
=  +(
+( +
+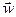 ); 2) $
); 2) $  ÎV, что "
ÎV, что "  ÎV
ÎV  +
+ =
= +
+ =
= ;
;
3) "  ÎV $ (-
ÎV $ (- ) ÎV такой, что
) ÎV такой, что  +(-
+(- )= (-
)= (- )+
)+ =
= ; 4) "
; 4) "  ,
, ÎV
ÎV  +
+  =
= +
+ ;
;
0’) Задана операция внешнего умножения скаляров (элементов из Р) на векторы (элементы из V) (то есть, что "lÎP, " ÎV, указанный вектор l
ÎV, указанный вектор l ÎV); 5) "l, m ÎP "
ÎV); 5) "l, m ÎP " ÎV (l×m)
ÎV (l×m) =l(m
=l(m );
);
6) "l, m ÎP " ÎV (l+m)
ÎV (l+m) =l
=l +m
+m ;
;
7) "lÎP " ,
, ÎV l(
ÎV l( +
+ )=l
)=l +l
+l ;
;
8) " ÎV 1
ÎV 1 =
= .
.
Пример. V=Mat{m×n|R}, U={A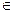 V| a11=0} является подпространством в V.
V| a11=0} является подпространством в V.
Пример: P[x] – линейное пространство, Pn[x] - линейное пространство, Pn[x]  P[x]
P[x]
Пример: 
Ранг системы векторов
Доказательство. Эти подсистемы линейно независимые и, по 3.9 они выявляются одна через вторую. Таким образом, 4.1 следует из 3.14. ■ Опр. 4.2. Количество векторов в МЛНП системы (1) называется рангом системы… Св-во 4.3. Когда данные системы векторов (1) и (2) Ранги систем векторов (1) и (2) равные тогда и только тогда, когда,…Базис линейного пространства. Определение и простейшие свойства
1) система (1) линейно независимая; 2) (условие полноты) "ÎV $l1, l2,…,lnÎP=l1+l2+ . . .+ln. Азн. 5.2. Количество векторов в базисе называется размерностью пространства V… Св-во. 5.3. Определение 5.2. корректное, то есть, что когда (2) и (1) - базисы V, тогда k=n. Доказательство. Все…Координаты вектора в базисе. Определение и свойства
Опр. 5.10. Упорядоченная n-ка (l1;...;ln)из расписания (3) называется координатами вектора в базисе (1). Координаты вектора записывают в строчку… Св-во 5. 11. Когда вектор имеет в базисе (1) столбец координат X=,тогда… Св-во 5.12. Когда в базисе (1) вектор имеет столбец координат X= а вектор имеет столбец координат Y=, тогда +имеет в…Матрица системы векторов. Определение и свойства.
Опр. 6.1. V - линейное пространство над P, dimV=n, данный базис V, ,(1) и произвольная система векторов (2) . Пусть "i=++… + = (3). Матрица… Пример 6.2. V2. – базис. В этом базисе система векторов ; ; имеет матрицу A=.… Опр. 6.4. Пусть (1) и ,,…,(4) - базисы пространства V. Матрица системы векторов (4) в базисе (1) называется матрицей…Матрица перехода от базиса к базису
Теорема 6.5. Матрица перехода от базиса к базису - невырожденная. Доказательство. (1) - базис, значит "k і А=()- матрица (4) в (1). Поскольку… Вывод.6.6. Матрицы перехода от (1) к (4) и от (4) к (1) - взаимно обратные.… Теорема 6.7. Когда А - матрица перехода от (1) к (4), и имеет в базисе (1) столбец координат , а в базисе (2) , тогда…Подпространства. Свойства. Линейная оболочка системы векторов
Ул.7.6. Когда U и W подпространства пространства V, тогда U∩W - подпространство пространства V. Доказательство. 1. Так как U і W, U∩W ,… 2. Когда и и U∩W,тогда по 7.2.2 +U и +W,откуда+U∩W. 3. Когда U∩W і λР, тогда по 7.2.3 λU и λW, значиться λU∩W■Фундаментальная система решений системы однородных линейных уравнений
Св-во 7.11.5. Если в (4) поочередно каждому придавать значение единицы, а остальным нули, то получим фундаментальную систему решение.… Следствие 7.11.6. Размерность пространства решений системы (1) равна числу…Линейные отображения. Определение, примеры, простейшие свойства
Азн.8.1. Пусть V, U -линейные пространства над P. Отображение f: V→U(1) называется линейным (гомоморфизмом линейная пространства), когда1)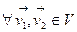
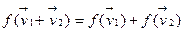 ; 2)
; 2) 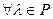
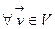
 .
.
Примеры: 1. V=R2, U=R1[x], f :V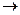 U:
U: .
.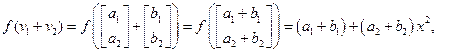

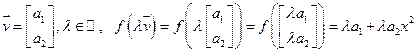
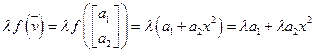 2. Поворот плоскости
2. Поворот плоскости  кругом пункта О.
кругом пункта О.
3. Нулевое отображение f :  . 4. Тождественное преобразование
. 4. Тождественное преобразование 
Св-во 8.2. Когда f :V U - линейное отображение, тогда: 1)
U - линейное отображение, тогда: 1)  ; 2)
; 2) 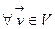 V
V  ; 3)
; 3)  P,
P, 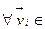 V
V 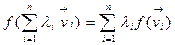 . Доказательство. 1)
. Доказательство. 1)  .
.
2)  . 3) ММИ по n. 1) n=1 – это 8.1.2.
. 3) ММИ по n. 1) n=1 – это 8.1.2.
2) n=2 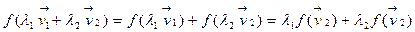 . Если св-во справедливо для n, то
. Если св-во справедливо для n, то
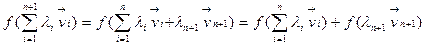
 ■
■
Теорема 8.3. ( Критерий линейности отображения) V, U-линейные пространства над P. Отображение f: V→U является линейным тогда и только тогда, когда 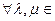 P,
P, 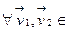 V
V  (2)
(2)
Доказательство. 1) Когда f - линейное, тогда (2) следует из 8.2.3. 2) Пусть исполняется (2), возьмем  , тогда
, тогда 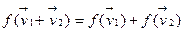 , значиться исполняется 8.1.1. Возьмем
, значиться исполняется 8.1.1. Возьмем  :
:  (по 8.2.1), значит исполняется 8.1.2. Таким образом, f - линейное отображение.■
(по 8.2.1), значит исполняется 8.1.2. Таким образом, f - линейное отображение.■
Теорема 8.4. V, U -линейные пространства над P. dimV=n, 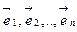 - произвольный базис V. Задание линейного отображения
- произвольный базис V. Задание линейного отображения  эквивалентно заданию образов элементов базиса
эквивалентно заданию образов элементов базиса 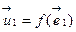 ,
, 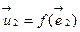 , . . . ,
, . . . ,  . Доказательство. 1) Когда задана линейное отображение, тогда
. Доказательство. 1) Когда задана линейное отображение, тогда  задан
задан 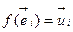 .
.
2) Пусть заданный 
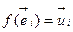 . Надо задать линейное отображение.
. Надо задать линейное отображение. 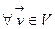 определяется в виде
определяется в виде 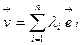 (поскольку
(поскольку 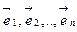 - базис). Укажем отображение
- базис). Укажем отображение 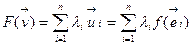 .
.
Докажем, что F - линейное отображение, и 
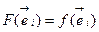 . Начнем доказательство из конца.
. Начнем доказательство из конца.  ,
, 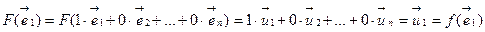 ,
, 
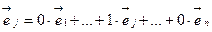 ,
,  . Докажем, что F - линейное. Проверим 8.3. Для произвольных векторов и скаляров
. Докажем, что F - линейное. Проверим 8.3. Для произвольных векторов и скаляров 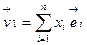 ,
,  ,
, 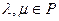
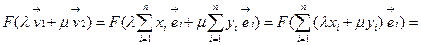
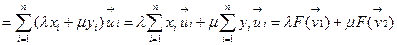 .■
.■
Линейные отображения, их связь с подпространствами и композиция
Опр. 8.7. Пусть f: V→U - линейное отображение, тогда является подпространством в , которое обозначается . Теорема. 8.8. Гомоморфный праобраз подпространства является подпространством,… Частные случаи получаются, когда взять или . ■Изоморфизм конечномерных векторных пространств
Пример 9.2. 1) - тождественное отображение. Биективность очевидна. Раньше показано, что линейно. 2) .Биективность очевидна. Св-во 9.3. Когда f:V→U- изоморфизм линейных просторов, тогда f -1:… . nИзоморфизм конечномерных пространств и системы векторов
Следствие 9.9. Пусть f: V→U - изоморфизм, тогда система векторов и либо обе линейно зависимы, либо обе линейно независимы. Доказательство:… Следствие 9.10. Если f: V→U - изоморфизм, то ранги обеих систем из… Следствие 9.11.: Пусть f: V→U - линейное отображение, - базис V, f является изоморфизмом, тогда и только тогда,…Матрица линейных отображений и ее свойства
Пример 10.2. . Покажем, что F – линейно. Линейность доказана. Построим матрицу F, соотв. (I)… Св-во 10.3. Пусть f: V→U - линейное отображение. (1) и (2) – базисы V и U, тогда f соотв. матрица А, отображение…Линейные операторы и их матрицы
Азн. 10.6. Когда V- линейное пространство над над Р, а f: V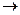 V - линейное отображение, тогда f называется линейным оператором, эндоморфизмам пространства ли V. Множество эндоморфизмов пространства V обозначается EndP(V), или End(V).
V - линейное отображение, тогда f называется линейным оператором, эндоморфизмам пространства ли V. Множество эндоморфизмов пространства V обозначается EndP(V), или End(V).
Опр. 10.7. Пусть  (1) - базис V, End(V) – множество всех изоморфизмов V. fÎEnd(V), тогда матрица системы векторов
(1) - базис V, End(V) – множество всех изоморфизмов V. fÎEnd(V), тогда матрица системы векторов  в базисе (1) наз. матрицей оператора f в базисе (1).
в базисе (1) наз. матрицей оператора f в базисе (1).
Пр. 10.8. 1) D:  :
:
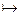
 . Эндоморфизм D в базисе 1, x, x2 имеет матрицу А=
. Эндоморфизм D в базисе 1, x, x2 имеет матрицу А=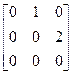
 . 2) Эндоморфизм
. 2) Эндоморфизм  – поворот
– поворот 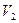 около пункта 0 на угол
около пункта 0 на угол 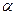 , в базисе
, в базисе  имеет матрицу
имеет матрицу 
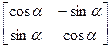 . 3) Найдем матрицу этого же эндоморфизма
. 3) Найдем матрицу этого же эндоморфизма 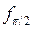 в базисе
в базисе 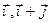 :
: 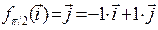 ;
;  . В итоге, эндоморфизм
. В итоге, эндоморфизм 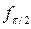 в базисе
в базисе 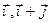 имеет матрицу
имеет матрицу 
 .
.
Св-во 10.9. Пусть f – линейное преобразование пространства в V. (1) – базис в V, тогда каждому fÎEnd(V) соотвествует матрице  - матрица f в базисе (1) и наоборот, каждой матрице А соответствует единственный линейный оператор fÎEnd(V), для которого А – его матрица в базисе (1). Доказательство: частный случай 10.3. n
- матрица f в базисе (1) и наоборот, каждой матрице А соответствует единственный линейный оператор fÎEnd(V), для которого А – его матрица в базисе (1). Доказательство: частный случай 10.3. n
Св-во 10.10. Пусть (1) – базис линейного пространства V, fÎEnd(V),  - матрица линейного оператора f в базисе (1). Если вектор V в базисе (1) имеет столбец координат Х, а f(v) имеет столбец координат Y, то Y=AX. Доказательство: частный случай 10.4. n
- матрица линейного оператора f в базисе (1). Если вектор V в базисе (1) имеет столбец координат Х, а f(v) имеет столбец координат Y, то Y=AX. Доказательство: частный случай 10.4. n
Пример 10.11. 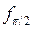 :V2
:V2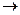 V2, найти
V2, найти 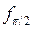 (
( ), где
), где  =
=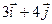 . Решение 1. Поскольку
. Решение 1. Поскольку 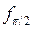 (
(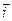 )=
)= ;
; 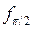 (
( )= -
)= - 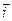 , то
, то 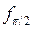 (
( ) =
) =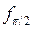 (
(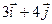 )= =3
)= =3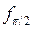 (
(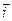 )+4
)+4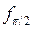 (
( ) =3
) =3 +4( –
+4( – 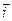 ) = – 4
) = – 4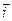 +3
+3 . Решение 2. В базисе
. Решение 2. В базисе 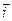 ,
, оператор
оператор 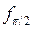 имеет матрицу А=
имеет матрицу А= , а вектор
, а вектор  имеет столбец координат Х=
имеет столбец координат Х= .
. 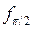 (
( ) в базисе
) в базисе 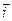 ,
, имеет столбец координат Y=АХ=
имеет столбец координат Y=АХ= ×
× =
=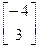 . – 4
. – 4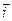 +3
+3 . Какие координаты имеет вектор
. Какие координаты имеет вектор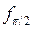 (
( ) в базисе
) в базисе
 =
=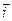 ,
,  =
=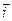 +
+ ? Решение 1. Достаточно найти координаты вектора -4
? Решение 1. Достаточно найти координаты вектора -4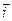 +3
+3 в базисе
в базисе  ,
, . Это можно сделать по определению координат вектора в базисе: –4
. Это можно сделать по определению координат вектора в базисе: –4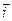 +3
+3 = х
= х +у
+у , –4
, –4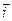 +3
+3 = х
= х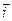 +у(
+у(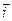 +
+ ), –4
), –4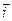 +3
+3 = (х+у)
= (х+у)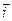 +у
+у . Поскольку
. Поскольку 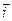 ,
, - базис,
- базис, 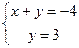 , то,
, то, 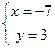 и
и  . Решение 2.
. Решение 2.  =
=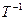 Х=
Х=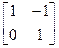 ×
× =
= . Оператор
. Оператор  имеет в базисе
имеет в базисе  ,
, матрицу В=
матрицу В=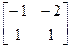 . Тады
. Тады 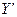 =В
=В =
=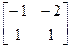 ×
× =
=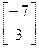 .
.
Лемма 11.7. Пусть матрицы С, DÎMat(m´n,P) такие, что для произвольного столбца ХÎMat(n´1,P) СХ=DX, (3) тогда С=D. Доказательство. Когда Х= , из равенства (3) очевидно получается, что в матрицах С и D первые столбцы равные. Когда Х=
, из равенства (3) очевидно получается, что в матрицах С и D первые столбцы равные. Когда Х= , получаем равенство вторых столбцов матриц С и D. Все соответствующие столбцы матриц С и D равные, значит С=D. n
, получаем равенство вторых столбцов матриц С и D. Все соответствующие столбцы матриц С и D равные, значит С=D. n
Теорема 10.13. Пусть (1) и 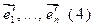 - базисы пространства V, Т – матрица перехода от (1) к (4). fÎEnd(V),
- базисы пространства V, Т – матрица перехода от (1) к (4). fÎEnd(V),
f имеет матрицу А в (1), f имеет матрицу В в (4), тогда В = Т –1 А Т. Доказательство: Пусть  имеет столбец координат
имеет столбец координат  По 10.10.
По 10.10. 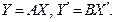
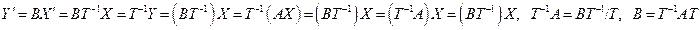 n
n
Опр.10.14. Квадратная матрица 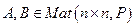 наз. сопряженной с помощью матрицы S, если
наз. сопряженной с помощью матрицы S, если 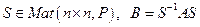 .
.
Следствие 10.15. А, В сопряжены тогда и только тогда, когда они являются матрицами одного и того линейного оператора в разных базисах. Доказательство: То, что матрицы одного линейного оператора в разных базисах сопряжены, доказано в 10.13. Обратно. Пусть А, В сопряжены. Рассмотрим произвольное линейное пространство V над Р dimV=n, 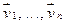 - произвольный базис V, тогда по 10.9. есть линейный оператор fÎEnd(V), который в этом базисе имеет матрицу А. Рассмотрим
- произвольный базис V, тогда по 10.9. есть линейный оператор fÎEnd(V), который в этом базисе имеет матрицу А. Рассмотрим 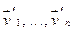 - базис, который в исходном базисе имеет матрицу S. По условию матрица S невырождена, тогда
- базис, который в исходном базисе имеет матрицу S. По условию матрица S невырождена, тогда 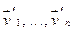 - базис V. По 10.13. f имеет
- базис V. По 10.13. f имеет 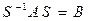 матрицу. n
матрицу. n
Ранг матрицы. Определение и свойства
Опр. 11.2. Пусть Если в матрице А выделить k строк и k столбцов, то на их пересечении будет стоять матрица размера Определитель этой матрицы… Опр. 11.3. Если в матрице А все миноры k-го порядка равны 0, то все миноры… Св-во 11.4. Если у матрицы А все миноры k-го порядка =0, то и у матрицы АТ все миноры k-го порядка =0. Доказательство.…Ранг матриц и системы линейных уравнений
Т. 11.19. Теорема Кронер-Капелли: Система линейных уравнений совместна , когда ранг матрицы коэффициентов равен рангу расширенной матрицы системы.… Т. 11.20. Структура решений систем линейных уравнений.Пусть дана система и… Следствие 11.21. Все решения системы АХ=В имеет вид Х*+ ХО ,т.е. принадлежит множеству , где V – пространство решение,…Евклидовы пространства. Определение и свойства
2) ÎV (+;)=(;)+(;), 3) ÎR ÎV (;)=(;), 4) ÎV (;)>0 , если . Простанство V, в котором заданно скалярное достояние,… Пример 12.2.1) V2 со скалярным произведением , который изучался в курсе… Св-во 12.3. В произвольной Евклидовом пространстве: 1) Îε (;)=(;)=;Норма вектора. Неравенство Коши-Буняковского. Угол между векторами.
Пример 12.6..1. В соотв. геометрическому определению длины вектора. 2. У С[a;b] =. Св-во 12.7.В Евклидовом пространстве ε: 1) = 0 т. и только тогда, когда… Доказ. 1)Если =, тогда ===0. Если , тогда >0, откда =>0.Геометрические теоремы в евклидовых пространствах
Теорема 12.17. (Неравенство треугольника в Евклидовом пространстве.) . Доказательство: Докажем правую часть неравенства: . Докажем правую часть неравенства: ; ; . При доказательстве два раза использовали неравенство Коши-Буняковского.■Ортогональные векторы и ортогональный базис.
Св-во 13.2.В Евклидовом пространстве ε: 1. Нулевой вектор и только он ортогональное само сам; 2. Нулевой вектор и только он ортогональный всем векторам; 3 . Когда… 1) Когда =, то по 12.7.1 (,)=()=0; а когда ≠, то по 12.7.4 (,)>0. 2) Когда =0, то по 12.7.1 (,)=(,)=0; а…Ортонормированный базис евклидова пространства.
Тэарэма 13.9.Базис (2) евклидового пространства εn является ортонормированным тогда и только тогда, когда ортогональное достояние произвольных… Откуда =1. Аналогично . Когда з (3)следует, что , то (2) – ортонормированный… Тэарэма 13.10.В каждой конечномерном евклидовом пространстве существует ортонормированный базис.Ортогональные операторы. Определение, примеры, свойства
ОПР .14.1.Пусть ε – Евклидовое пространство. Лин. Преобразование f:ε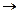 ε наз. ортогональным, если
ε наз. ортогональным, если  Îε
Îε 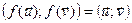 .
.
Приметр14.2. В Евклидовом пространстве V2 со сколярным произведением 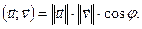 оператор f: V2
оператор f: V2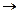 V2 является ортогональным.
V2 является ортогональным.
СВ-во.14.3.Если f: ε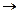 ε – ортогональный оператор, тогда: 1) f сохраняет норму, т.е.
ε – ортогональный оператор, тогда: 1) f сохраняет норму, т.е.
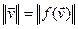 ); 2) f сохроняет угол между векторами, т.е.
); 2) f сохроняет угол между векторами, т.е. 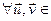 ε{
ε{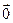 }
} 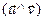 =
= ).
).
Д-во. 1)  , значыцца
, значыцца 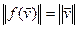 .
.
2) 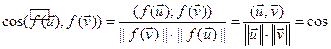
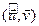 , адкуль
, адкуль 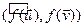 =
=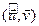 .■
.■
Св-во14.4.Ортогональный оператор явл. ортоморфизмом пр-ва, т.е. биективным, лин. отображ
Ортогональные операторы и ортогональные матрицы
ОПР .14.1.Пусть ε – Евклидовое пространство. Лин. Преобразование f:ε ε наз. ортогональным, если
ε наз. ортогональным, если  Îε
Îε 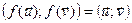 .
.
Опр.14.5.Матрица AÎMat(n´n;R) наз. ортогональной, если 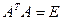 . Прыклад14.6.
. Прыклад14.6.
Лемма 14.7.Если A, BÎMat(n´n;R) і  X, YÎRn
X, YÎRn  тады
тады  .Доказ.
.Доказ.  . Т.к
. Т.к 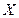 ,
, 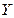 - любые, рассиотрим
- любые, рассиотрим 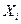 -столбец, у которого і-ы элемент равен 1, а все остальные 0. Так определим и
-столбец, у которого і-ы элемент равен 1, а все остальные 0. Так определим и  трудно заметить, что
трудно заметить, что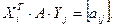 . А это значит, что
. А это значит, что 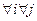
 , значит ,
, значит ,  .■
.■
Св-во14.8.Ортогональный оператор Евклидового пространства в ортонормированном базисе имеет ортогональную матрицу. До-во. Пусть 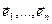 ортанармированный базис εn, f:εn
ортанармированный базис εn, f:εn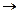 εn - ортогональный оператор и А- его матрица в этом базисе. Рассмотрим произвольные векторы
εn - ортогональный оператор и А- его матрица в этом базисе. Рассмотрим произвольные векторы  Îεn, которые имеют столбцы координат
Îεn, которые имеют столбцы координат 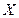 ,
, 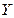 соответственно в данном базисе. Тогда векторы
соответственно в данном базисе. Тогда векторы  і
і 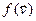 имеют столбцы координат
имеют столбцы координат  і
і 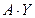 соответственно. Из ортогональности f по 14.7 следует, что
соответственно. Из ортогональности f по 14.7 следует, что 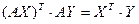 ,
, 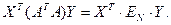 Из леммы 15.6 следует, что
Из леммы 15.6 следует, что 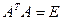 .■
.■
Св-во 14.10. Оператор f ортогонален тогда и только тогда, когда его матрица в ортонормированном базисе ортогональна. Доказательство: Утверждение, что если f – ортогонально, следует, что А – ортогональна (по 14.8.). Обратно: пусть есть ортонормированный базис, А – ортогональная матрица, тогда есть оператор f. Пусть 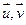 в этом базисе имеют столбцы координат Х и Y. Тогда
в этом базисе имеют столбцы координат Х и Y. Тогда 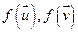 имеют столбцы координат АХ и AY. Тогда
имеют столбцы координат АХ и AY. Тогда  ■
■
Ортогональные операторы, матрицы и системы векторов
Св-во 14.11: Линейный оператор  в Евклидовом пр-ве
в Евклидовом пр-ве 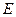 ортонормирован тогда и только тогда, когда он переводит ортонормированный базис в ортонормированный базис. Доказательство: Пусть fортогонален.
ортонормирован тогда и только тогда, когда он переводит ортонормированный базис в ортонормированный базис. Доказательство: Пусть fортогонален.  - ортонормированный базис.
- ортонормированный базис.  - ортонормированный базис. f– ортогонален, значит сохраняет норму.
- ортонормированный базис. f– ортогонален, значит сохраняет норму. 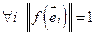 . fсохраняет угол, значит векторы
. fсохраняет угол, значит векторы 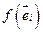 попарно ортогональны. Тогда они линейно независимы, значит линейное пространство образует базис. Обратно: пусть
попарно ортогональны. Тогда они линейно независимы, значит линейное пространство образует базис. Обратно: пусть  - ортонормированный базис.
- ортонормированный базис.  - ортонормированный базис. Пусть
- ортонормированный базис. Пусть 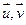 имеют столбцы координат Х и Y. Тогда
имеют столбцы координат Х и Y. Тогда 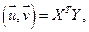
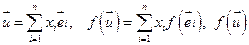 имеет столбец Х в базисе
имеет столбец Х в базисе  . Аналогично
. Аналогично 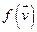 имеет Yв том же ортонормированном базисе. Получим
имеет Yв том же ортонормированном базисе. Получим  ■
■
Св-во 14.12. Композицияортогональный отображений ортогональна отображению. Доказательство: 
 ■
■
Св-во 14.13. Матрица А является ортогональной тогда и только тогда, когда  . Доказательство:
. Доказательство:  ,
, 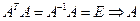 - ортогональная.
- ортогональная. 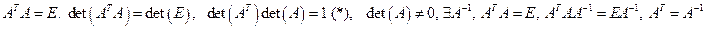 ■
■
Следствие 14.14. Оперделитель ортогональной матрицы равен 1 или –1. Доказательство: Возьмем (*). 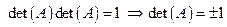 ■
■
Сумма линейных операторов и ее свойства
Опр. 15.1. Путь f1 і f2 линейные операторы V, тогда их суммой называют отображение
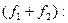 V
V 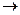 V
V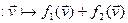 (2)
(2)
Св-во 16.2.Сумма линейных операторов является линейным оператором. Док-во. Используем теорему о критерии линейности:  V
V  P
P 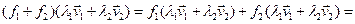
 (в первой и последней равенствах использовали определение 16.1, а во второй - теорему 8.3). ■
(в первой и последней равенствах использовали определение 16.1, а во второй - теорему 8.3). ■
Св-во15.3.Когда линейные операторы f1 и f2 имеют в базисе (1) матрицы A1 и A2, тогда линейный оператор f1+ f2 мои в этом базисе матрицу A1+ A2. Док-во. Пусть произвольный вектор  , векторы
, векторы  имеют в базисе
имеют в базисе  (1) соответствующие столбцы координат . Х,
(1) соответствующие столбцы координат . Х,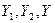 . Тогда
. Тогда 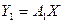 ;
; 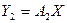 . По определению 15.1
. По определению 15.1  . Отсюда следует, что
. Отсюда следует, что 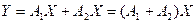 . Из замечания о единственности матрицы линейного оператора следует, что
. Из замечания о единственности матрицы линейного оператора следует, что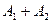 – матрица линейного оператора
– матрица линейного оператора  в базисе (1).■
в базисе (1).■
Св-во.15.4.Множество End(V) с операцией сложения лин. операторов явл. аддитивной(+/-), коммутативной группой. Доказательство: 1) Докажем ассоциативность операции сложения (1).:  V
V 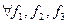 ÎEnd(V)
ÎEnd(V)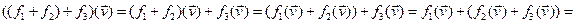
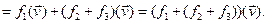 Так как
Так как  – произвольный, доказали равенство отображений:
– произвольный, доказали равенство отображений:  . 2) Докажем коммутативность сложения операторов:
. 2) Докажем коммутативность сложения операторов:  V
V  End(V)
End(V) 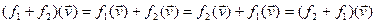 , значыцца,
, значыцца, 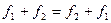 .
.
3) Очевидно, что нулевое отображение  V
V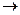 V
V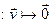 принадлежит End(V) и является нейтральным относительно сложения элементов в End(V):
принадлежит End(V) и является нейтральным относительно сложения элементов в End(V):  V
V 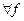 ÎEnd(V)
ÎEnd(V)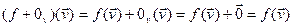 . Отсюда следует
. Отсюда следует  . 4) Докажем, что для произвольного fÎEnd(V)отображение (–f):V
. 4) Докажем, что для произвольного fÎEnd(V)отображение (–f):V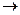 V
V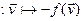 является линейным оператором, и что
является линейным оператором, и что  .
.  V
V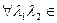 P
P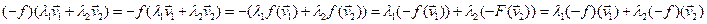
Значит, 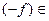 End(V).
End(V).  V,
V, 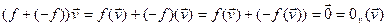 , из чего следует, что
, из чего следует, что  .■
.■
Св-во. 15.5.Когда dim(V)=n, тогда End(V) и Mat(n n;P) являются изоморфными аддитивными группами.
Доказательство. В свойства 11.4 доказали, что когда фиксированный базис (1) в V, то сущнствует биективное отображение F: Mat(n´n;P)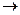 End(V). Из свойства 15.3 следует , что "A1,A2Î Mat(n´n;P) F(A1+A2)= F(A1)+F(A2), таким образом, F - изоморфизм аддитивных групп End(V) і Mat(n´n;P).■
End(V). Из свойства 15.3 следует , что "A1,A2Î Mat(n´n;P) F(A1+A2)= F(A1)+F(A2), таким образом, F - изоморфизм аддитивных групп End(V) і Mat(n´n;P).■
Умножение линейного оператора на скаляр
Орп. 15.6.V – лин. пространство над P, fÎEnd(V), 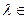 P. Произведением скаляра
P. Произведением скаляра 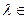 на эндоморфизм f называется отображение
на эндоморфизм f называется отображение 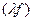 :V
:V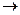 V:
V: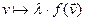 .
.
Св-во 15.7  ÎEnd(V).До-во.
ÎEnd(V).До-во. 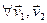 ÎV
ÎV P
P 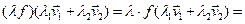

значит, fÎEnd(V). ■
Св-во 15.8. 1) 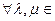 P,
P, 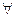 fÎEnd(V)
fÎEnd(V)  ; 2)
; 2) 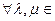 P,
P, 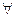 fÎEnd(V)
fÎEnd(V) 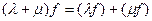 ;
;
3) 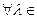 P,
P, 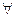 f1, f2ÎEnd(V)
f1, f2ÎEnd(V) 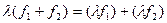 ; 4)
; 4) 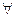 fÎEnd(V) 1× f = f.
fÎEnd(V) 1× f = f.
Доказ.1)  V
V 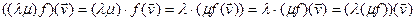 , значит,
, значит,  .
.
2) 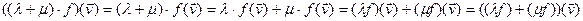 ,
,
откуда 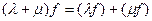 . 3)
. 3) 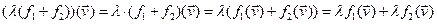
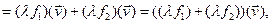 значит
значит 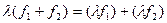 . 4)
. 4) . ■
. ■
Св-во 15.9.End(V) является линейным пространством над P. Доказательство. Свойства 1)-4) определения 1.1 доказана в 15.4, а свойства 5)-8) этого определения рассматривались в 15.8. ■
Св-во 15.10.Калі эндамарфізм fÎEnd(V) мае ў базісе (1) матрыцу А, тады эндамарфізм 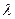 f мае ў базісе (1) матрыцу
f мае ў базісе (1) матрыцу 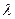 А. Доказ.Когда произвольный вектор
А. Доказ.Когда произвольный вектор  и векторы f(
и векторы f( ), (
), (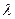 f)(
f)( ) имеют в базисе (1)столбцы координат соответственно Х, Y,
) имеют в базисе (1)столбцы координат соответственно Х, Y,  , тогда по определению 16.6,
, тогда по определению 16.6,  значит,
значит, 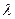 А – матрица (
А – матрица (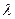 f) в базисе (1).■
f) в базисе (1).■
Т. 15.11.Если dim(V)=n, тогда лин. пространство End(V) і Mat(n´n;P) изоморфное. Доказ. Рассмотрим ту же биекцию F: Mat(n´n;P)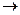 End(V), что и в 15.5. То, что F сохраняет сложение, доказана в 15.5. То, что
End(V), что и в 15.5. То, что F сохраняет сложение, доказана в 15.5. То, что 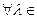 P,
P, 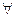 AÎEnd(V)
AÎEnd(V) 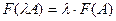 , следует из 16.8 и замечания о единственности матрицы оператора в базисе.■
, следует из 16.8 и замечания о единственности матрицы оператора в базисе.■
Вывод. 15.12.Калі dim(V)=n, тады dim (End(V))=n2. Доказ.Очевидно, что dim(Mat(n´n;P))=n2, а так как изоморфные пространства имеют равные измеримости, тогда dim(End(V))= n2.■
Кольцо эндоморфизмов линейного пространства
Св-во.16.14.Калі dim(V)=n, End(V) і маюць у базісе (1)адпаведныя матрыцы тады мае ў базісе (1) матрыцу . Доказ.Когда произвольный вектор и вектор і… Св-во.16.15.End(V) относительно операций сложения операторов и композиции… . Значит .Линейные алгебры
Прыклад 16.17.1) С над R. 2) Mat(n´n:P). 3) P[x]. Св-во.16.18.Если V – линейное пространство над Р, то End(V) – лінейная алгебра…Инвариантные подпространства. Собственные векторы. Простейшие свойства
Азн.16.1. fÎEnd(V). Подпространство U пространства V называется инвариантной относительно f (или f - инвариантной), когда  ÎU
ÎU  ÎU (1)
ÎU (1)
Прыклад 16.2.1. V=V2, prx – проекция на ось Ox. U1=R R} - инвариантная относительно prx подпространство, так как
R} - инвариантная относительно prx подпространство, так как 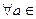 R,
R,  U1. U2=R
U1. U2=R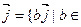 R} - также инвариантные относительно prx подпространство, так как
R} - также инвариантные относительно prx подпространство, так как 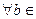 R,
R, 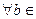 R
R 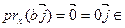 U2.
U2. 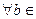 R
R 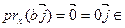 U2.
U2.
16.2.2. V=V3, f – поворот вокруг оси Oz на угол 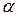 . f- инвариантными являются UzіUxoy - просторо векторов плоскости xOy.
. f- инвариантными являются UzіUxoy - просторо векторов плоскости xOy.
16.2.3. Для оператора D деференцирования пространства P[x] для произвольного натурального n пространства
Pn[x] является D-инвариантными.
16.2.4. Для произвольного fÎEnd(V) подпространства 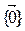 і V являются f - инвариантными. Они называются тривиальными.
і V являются f - инвариантными. Они называются тривиальными.
Св-во 16.3 Когда fÎEnd(V), U1 и U2 f - инвариантные подпространства, тогда U1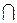 U2 также f- инвариантное подпространство. Доказ. Рассмотрим
U2 также f- инвариантное подпространство. Доказ. Рассмотрим 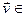 U1
U1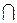 U2. То
U2. То 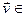 U1 откуда следует, что
U1 откуда следует, что  ÎU1. Аналогично,
ÎU1. Аналогично,  ÎU2, ■
ÎU2, ■
Азн. 16.4.Ненулевой вектор  ÎV называется собственным вектором оператора fÎEnd(V), когда существует
ÎV называется собственным вектором оператора fÎEnd(V), когда существует 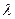 ÎP такой, что f
ÎP такой, что f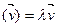 . При этом говорят, что
. При этом говорят, что 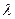 - собственная значимость линейного оператора f, которое соответствует вектору
- собственная значимость линейного оператора f, которое соответствует вектору 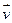 .
.
Прыклад 16.5.У линейного оператора prx линейного пространства V2 вектор 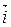 является собственным из собственной значимостью 1, поскольку
является собственным из собственной значимостью 1, поскольку 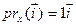 . Т.к.
. Т.к. 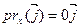 , вектор
, вектор  - собственный, которому соответствует собственная значимость 0.
- собственный, которому соответствует собственная значимость 0.
Св-во 16.6.Когда  - собственный вектор линейного оператора fÎEnd(V), которому соответствует собственная значимость
- собственный вектор линейного оператора fÎEnd(V), которому соответствует собственная значимость 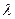 ÎP, тогда для произвольного
ÎP, тогда для произвольного 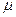 ÎP{0} вектор
ÎP{0} вектор 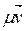 также является собственным вектором оператора f, которому также соответствует собственная значимость
также является собственным вектором оператора f, которому также соответствует собственная значимость 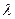 . Доказ. По условию
. Доказ. По условию 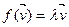 . Тогда очевидно, что
. Тогда очевидно, что  і
і  .■
.■
Вынік 16.7Когда  - собственный вектор линейного оператора fÎEnd(V), которому соответствует собственная значимость
- собственный вектор линейного оператора fÎEnd(V), которому соответствует собственная значимость 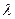 , тогда подпространство P
, тогда подпространство P ={
={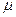
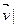
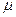 ÎP} является f-инвариантной и каждый ненулевой вектор этого пространства является собственным вектором этого пространства является собственным вектором f, которому соответствует собственная значимость
ÎP} является f-инвариантной и каждый ненулевой вектор этого пространства является собственным вектором этого пространства является собственным вектором f, которому соответствует собственная значимость  . Доказ. Следует из 17.6 и того, что f
. Доказ. Следует из 17.6 и того, что f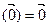 .■
.■
Азн. 16.8 Пусть  (3) -базис пространства V, fÎEnd(V) і А=
(3) -базис пространства V, fÎEnd(V) і А=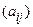 – матрица оператора f в базисе (3).Характеристическим полиномам матрицы А, а также характеристическим полиномамfназывается полином
– матрица оператора f в базисе (3).Характеристическим полиномам матрицы А, а также характеристическим полиномамfназывается полином
 (4).
(4).
Характеристические многочлены и собственные числа
(4). Св-во 16.9 Характеристические многочлены сопряжены, матриы равны. Доказ. Пусть… ■Диагональные матрицы линейных операторов
Св-во 16.14. Пусть dimV=n. Линейный оператор f имеет в некотором базисе диагональную матрицу тогда и только тогда, когда это базис из собственных векторов. Доказательство: Пусть  -базис из собственных векторов,
-базис из собственных векторов,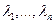 -собственные значения, тогда
-собственные значения, тогда 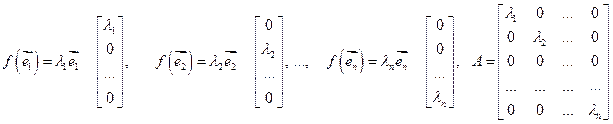 .Обратно. Пустьв базисе
.Обратно. Пустьв базисе  оператор f имеет матрицу
оператор f имеет матрицу 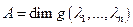
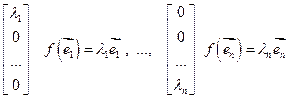 ■
■
Св-во 16.15. Собственные векторы линейного оператора, которые соотвествуют попарно неравным соотв. значениям, линейнонезависимы. Доказательство: ММИ по k – число векторов.  ,
, 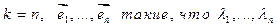 попарно различны, то она линейно независима.
попарно различны, то она линейно независима. 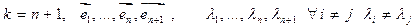

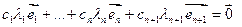 .Равенство (*) умножим на
.Равенство (*) умножим на 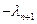 и прибавим к последнему равенству.
и прибавим к последнему равенству.
По посылке  - лин. независимые.
- лин. независимые. 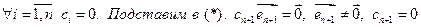 . Все коэффициенты в (*) равны нулю. Значит система векторов линейно независима. ■
. Все коэффициенты в (*) равны нулю. Значит система векторов линейно независима. ■
Т. 16.16. Пусть 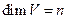 и линейный операторf имеет n попарно неравных собственных значений, тогда существует базис, в котором оператор f имеет диаональную матрицу. Доказательство: Если
и линейный операторf имеет n попарно неравных собственных значений, тогда существует базис, в котором оператор f имеет диаональную матрицу. Доказательство: Если 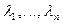 -попарно неравные собственные значения f, то соотв. собственным векторам
-попарно неравные собственные значения f, то соотв. собственным векторам 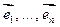 , которые по 16.15. линейно независимы. n линейно независимых векторов линейного пространства составляет базис из собственных векторов оператора f, тогда по 16.14. f в этом базисе диагональна. ■
, которые по 16.15. линейно независимы. n линейно независимых векторов линейного пространства составляет базис из собственных векторов оператора f, тогда по 16.14. f в этом базисе диагональна. ■
Следствие 16.17. Пусть 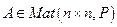 и имеет n попарно неравных собственных значений, тогда существует матрица
и имеет n попарно неравных собственных значений, тогда существует матрица 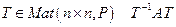 - диагональная. Доказательство: Рассмотрим V, dimV=n. Фиксируем в нем произвольный базис
- диагональная. Доказательство: Рассмотрим V, dimV=n. Фиксируем в нем произвольный базис 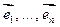 .Тогда существует линейный оператор
.Тогда существует линейный оператор 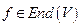 , который в этом базисе имеет операцию А. Собственное значение А и f совпадают, значит f имеет n попарно неравных собственных значений, тогда по 16.16. существует новый базис
, который в этом базисе имеет операцию А. Собственное значение А и f совпадают, значит f имеет n попарно неравных собственных значений, тогда по 16.16. существует новый базис 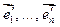 ,в котором матрица В оператора f диагональна. Возьмем T – матрицу перехода от старого базиса к новому.
,в котором матрица В оператора f диагональна. Возьмем T – матрицу перехода от старого базиса к новому.  диагональная. ■
диагональная. ■
Самосопряженные операторы, их свойства, матрицы, собственные векторы, примеры.
Опр. 17.1. ε – Евклидово пространство. Оператор fÎEnd(ε) наз. Самосопряженным , если 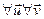 Îε
Îε  .
.
Пример17.2. 1. Очевидно, что тождественный оператор является самосопряженным. 2. В V2 рассмотрим оператор Pr x проектирования на ось Ox. Очевидно, что 
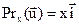 . Тогда
. Тогда 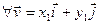
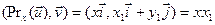 ,
, 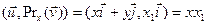 і
і 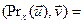
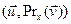 . Таким образом, доказали, что Prx - самосопряженный оператор.
. Таким образом, доказали, что Prx - самосопряженный оператор.
Св-во17.3. Когда f - самосопряженный оператор пространства ε, UÌε -является f-инвариантным подпространством, тогда ортогональное дополнение к U U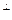
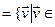 ε
ε  ÎU
ÎU 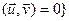 является f-инвариантным подпространством.Доказательство. Сначала докажем, что U
является f-инвариантным подпространством.Доказательство. Сначала докажем, что U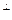 - подпространство в ε.
- подпространство в ε.  U
U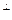 ,
,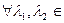 R,
R, 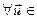 U
U  , значит,
, значит, 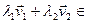 U
U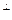 . По критерию подпространства следует, что U
. По критерию подпространства следует, что U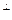 - подпространство в ε. Т.к.
- подпространство в ε. Т.к. 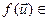 U,
U,  . Из самосопряженности оператора f следует, что
. Из самосопряженности оператора f следует, что  , значит
, значит 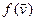 ÎU
ÎU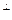 і U
і U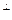 является f-инвариантным подпространством.n
является f-инвариантным подпространством.n
Св-во 17.4.Если линейный операторf–самосопряженный оператор пространства ε,А–его матрица в ортонормированном базисе, тогда А=АТ (1).Матрицы, которые удовлетворяют равенству (1) называются симметричными. Доказательство. Фиксируем произвольный ортонормированный базис в ε. Пусть в этом базисе f мои матрицу А, произвольные векторы 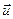 и
и  имеют столбцы координат X и Y. Тогда векторы
имеют столбцы координат X и Y. Тогда векторы 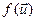 и
и 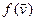 имеют столбцы координат AX и AY. По свойству 14.7
имеют столбцы координат AX и AY. По свойству 14.7  =(AX)TY =X TA TY, і
=(AX)TY =X TA TY, і  =X TAY. С самосопряженности f следует, что X TA TY=X TAY. Так как X и Y - произвольные столбцы, из последнего равенства по лемме 15.6 следует, что AT=A.n
=X TAY. С самосопряженности f следует, что X TA TY=X TAY. Так как X и Y - произвольные столбцы, из последнего равенства по лемме 15.6 следует, что AT=A.n
Св-во17.5. Когда 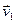 и
и 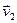 - собственные векторы самосопряженного оператора f, которым соответствуют неровные реальные собственные значимости
- собственные векторы самосопряженного оператора f, которым соответствуют неровные реальные собственные значимости  і
і  , тогда векторы
, тогда векторы 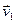 и
и 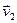 взаимообратные.
взаимообратные.
Доказательство. Так как f – самосопряженный оператор,  ,
, 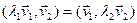 ,
, 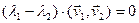 . По условию
. По условию 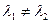 , значит,
, значит, 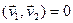 .n
.n
Собственные числа самосопряженных операторов
Лемма 17.6. У любого линейного оператора вещественного пространства есть инвариантное подпространство размерности 1 или 2. Доказательство:  . Фиксируем произвольный базис. Оператор f в нем имеет матрицу
. Фиксируем произвольный базис. Оператор f в нем имеет матрицу  . Рассматриваем этот многочлен как многочлен с комплексными коэффициентами. По основной теореме алгебры этот многочлен имеет корень
. Рассматриваем этот многочлен как многочлен с комплексными коэффициентами. По основной теореме алгебры этот многочлен имеет корень  . Если
. Если 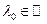 , то он соответствует некоторому
, то он соответствует некоторому  и
и  - пространство инвариантно относительно f.
- пространство инвариантно относительно f.  . Пусть
. Пусть 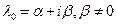 . Рассмотрим систему линейных уравнений над полем комплексных чисел
. Рассмотрим систему линейных уравнений над полем комплексных чисел 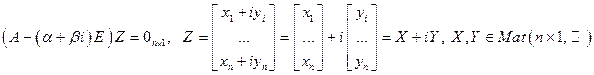
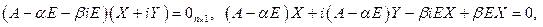
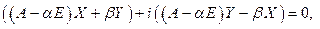 т.к. справа – действительная матрица, то
т.к. справа – действительная матрица, то 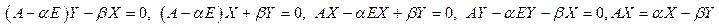
 . Рассмотрим векторы
. Рассмотрим векторы 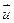 и
и  , которые в этом же базисе, где брали матрицу А, имеют столбцы координат Х и Y, тогда АХ и АY – столбцы координат
, которые в этом же базисе, где брали матрицу А, имеют столбцы координат Х и Y, тогда АХ и АY – столбцы координат 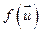 и
и 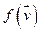 в этом же базисе.
в этом же базисе. 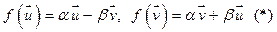 . Рассмотрим линейную оболочку
. Рассмотрим линейную оболочку 
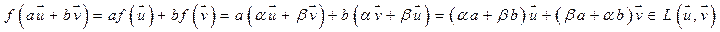
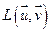 - подпространство инвариантное относительно f.
- подпространство инвариантное относительно f. 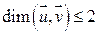 . ■
. ■
Свойство 17.7. Все собственные числа самосопряженного оператора - вещественные. Доказательство. От противоположного. Пусть f собственное число  , где
, где 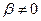 . Из доказательства леммы 17.6 следует,
. Из доказательства леммы 17.6 следует,
что Г ненулевые векторы 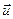 и
и  :
:  .
.  ;
;  ;
; 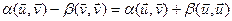 ;
; 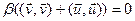 . Но
. Но  , получили противоречие. n
, получили противоречие. n
Теорема 17.8. f – самосопряженный оператор 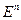 , тогда существует ортонормированный базис
, тогда существует ортонормированный базис 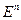 из собственных векторов f. Доказательство: ММИ по n. Если n=1, верно, т.к. любое линейное преобразование одномерного пространства
из собственных векторов f. Доказательство: ММИ по n. Если n=1, верно, т.к. любое линейное преобразование одномерного пространства 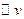 есть умножение на скаляр. Пусть верно для n+1.
есть умножение на скаляр. Пусть верно для n+1. 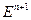 . Возьмем произвольное собственное значение
. Возьмем произвольное собственное значение  , которое соответствует
, которое соответствует 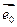 .
.  Известно, что
Известно, что 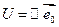 - одномерное собственное пространство f. Рассмотрим
- одномерное собственное пространство f. Рассмотрим 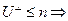 по посылке индукции.
по посылке индукции. 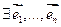 - ортонормированный базис из собственных векторов f. Покажем, что
- ортонормированный базис из собственных векторов f. Покажем, что 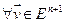 разлагается в сумму векторов
разлагается в сумму векторов 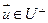 и вектора
и вектора 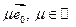 .
. 
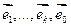 - базис
- базис 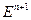 . Покажем это:
. Покажем это:  разлагается по базису
разлагается по базису  разлагается по
разлагается по 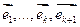 . Значит система линейно независима и она является ортонормированным базисом из собственных векторов f. n
. Значит система линейно независима и она является ортонормированным базисом из собственных векторов f. n
Св-во 17.9. Для любой симметричной матрицы А существует ортогональная матрица Т такая, что  - диагональная. Доказательство: Пусть
- диагональная. Доказательство: Пусть 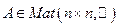 . Рассмотрим
. Рассмотрим 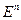 . Фиксируем в нем
. Фиксируем в нем  . Рассмотрим оператор f, который в этом базисе имеет матрицу А. Базис ортонормированный. Матрица симметричная, значит линейный оператор самосопряжен (по 17.4.). По 17.8. существует ортонормированный базис
. Рассмотрим оператор f, который в этом базисе имеет матрицу А. Базис ортонормированный. Матрица симметричная, значит линейный оператор самосопряжен (по 17.4.). По 17.8. существует ортонормированный базис  из собствееных векторов оператора f, в котором оператор f имеет матрицу
из собствееных векторов оператора f, в котором оператор f имеет матрицу 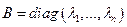 . Возьмем матрицу Т перехода от исходного базиса к базису из собственных векторов. Т.к. оба базиса ортонормированных, то Т – ортагональная.
. Возьмем матрицу Т перехода от исходного базиса к базису из собственных векторов. Т.к. оба базиса ортонормированных, то Т – ортагональная.  n
n
Квадратичные формы. Матрицы замены
Свойство 18.2. Если отождествить действительное число и матрицу , тогда F () =(2), где, , где - коэффициенты квадратичной формы, матрица А… Пример 18.3. Квадратичная форма имеет матрицу A = . Квадратычная форма имеет матрицу A = .Приведение квадратичной формы к каноническому виду
Теорема 19.9. Для каждой квадратичной формы существует замена, которая приводит форму к каноническому виду, причем ее можно выбрать так, что матрица… Пример 18.10., , , . Пронормируем векторы и и получим векторы , которые имеют…– Конец работы –
Используемые теги: определение, меры, Простейшие, Свойства, ных, пространств0.102
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Определение, примеры и простейшие свойства линейных пространств
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов