Частные случаи расположения плоскости.
Рассмотрим общее уравнение плоскости: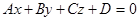 1.Если
1.Если 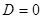 , то уравнение примет вид
, то уравнение примет вид 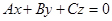 , координаты точки
, координаты точки 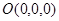 удовлетворяют этому уравнению, значит плоскость проходит через начало координат.
удовлетворяют этому уравнению, значит плоскость проходит через начало координат.
2.Если 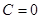 , то уравнение будет иметь вид
, то уравнение будет иметь вид 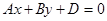 , тогда вектор нормали к плоскости
, тогда вектор нормали к плоскости  будет перпенди-кулярен оси
будет перпенди-кулярен оси 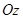 , значит данная плоскость параллельна оси
, значит данная плоскость параллельна оси 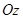 .
.
3.Аналогично, при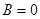 плоскость будет параллельна оси
плоскость будет параллельна оси 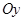 .
.
4. При 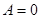 плоскость будет параллельна оси
плоскость будет параллельна оси 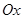 .
.
5.Если 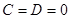 , то уравнение плоскости примет вид
, то уравнение плоскости примет вид 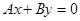 , то есть плоскость проходит через начало коорди-нат и параллельна оси
, то есть плоскость проходит через начало коорди-нат и параллельна оси 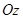 , значит плоскость проходит через ось
, значит плоскость проходит через ось 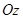 .
.
6.Если 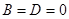 , то плоскость проходит через ось
, то плоскость проходит через ось 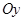 .
.
7.Если 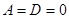 , то плоскость проходит через ось
, то плоскость проходит через ось 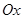 .
.
8.Если 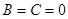 , то уравнение плоскости будет иметь вид
, то уравнение плоскости будет иметь вид 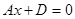 , вектор нормали к плоскости
, вектор нормали к плоскости 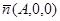 перпенди-кулярен плоскости
перпенди-кулярен плоскости  , следовательно, данная плоскость будет параллельна плоскости
, следовательно, данная плоскость будет параллельна плоскости 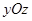 .
.
9.Если 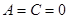 , то плоскость параллельна плоскости
, то плоскость параллельна плоскости 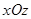 .
.
10.Если 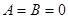 , то плоскость параллельна плоскости
, то плоскость параллельна плоскости 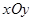 .
.
11.Если 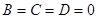 , то уравнение плоскости
, то уравнение плоскости 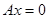 или
или 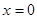 , эта плоскость проходит через начало координат и парал-лельна плоскости
, эта плоскость проходит через начало координат и парал-лельна плоскости 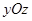 , то есть это координатная плоскость
, то есть это координатная плоскость 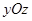 .
.
12.Если 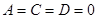 , то есть
, то есть 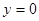 - это уравнение коорди-натной плоскости
- это уравнение коорди-натной плоскости 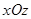 .
.
13.Если 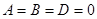 , то есть
, то есть 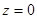 - это уравнение коор-динатной плоскости
- это уравнение коор-динатной плоскости 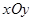 .
.
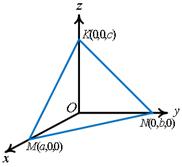
Рис.2
Пусть плоскость не параллельна ни одной из осей, тогда эта плоскость отсекает на осях координат отрезки 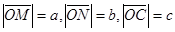 (рис.2). Воспользуемся общим уравнением плоскости (4) , где
(рис.2). Воспользуемся общим уравнением плоскости (4) , где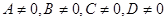 . Найдем коэффициенты уравнения, используя координаты точек пересечения плоскости
. Найдем коэффициенты уравнения, используя координаты точек пересечения плоскости 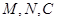 с осями координат. Так как эти точки лежат в плоскости, то их координаты удовлетворяют уравнению (4), следовательно,
с осями координат. Так как эти точки лежат в плоскости, то их координаты удовлетворяют уравнению (4), следовательно, 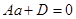 , откуда
, откуда 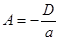 ,
,
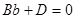 , тогда
, тогда 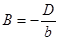 и
и 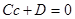 , тогда
, тогда 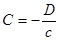 . Подставляя эти соотношения в (4), получим:
. Подставляя эти соотношения в (4), получим: 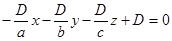 , так как
, так как 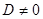 , разделим это равенство на
, разделим это равенство на 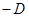 и получим:
и получим:
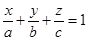 (7)
(7)
Это уравнение плоскости в отрезках; числа 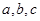 показывают, какие отрезки на осях координат отсекает данная плоскость.
показывают, какие отрезки на осях координат отсекает данная плоскость.
Пусть известны координаты вектора нормали к плоскости 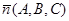 и координаты точки
и координаты точки 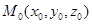 , которая принад-лежит плоскости. Надо составить уравнение данной плоскости.
, которая принад-лежит плоскости. Надо составить уравнение данной плоскости.
Возьмем произвольную точку плоскости 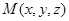 , тогда век-тор
, тогда век-тор 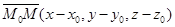 тоже будет принадлежать плос-кости, вектор нормали, перпендикулярный плоскости,перпенди-
тоже будет принадлежать плос-кости, вектор нормали, перпендикулярный плоскости,перпенди-
кулярен любому вектору, лежащему в этой плоскости, то есть 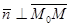 , а тогда скалярное произведение этих векторов рав-но нулю:
, а тогда скалярное произведение этих векторов рав-но нулю:
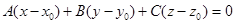 (8)
(8)
Получили уравнение плоскости, проходящей через заданную точку с заданным вектором нормали. При всевозможных значениях 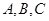 равенство (8) определяет совокупность всех плоскостей, проходящих через точку
равенство (8) определяет совокупность всех плоскостей, проходящих через точку 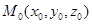 , и называ-ется уравнением связки плоскостей, проходящих через задан-ную точку.
, и называ-ется уравнением связки плоскостей, проходящих через задан-ную точку.
Пример 1. Даны точки 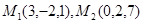 . Составить уравнение плоскости, проходящей через точку
. Составить уравнение плоскости, проходящей через точку 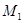 и перпен-дикулярной вектору
и перпен-дикулярной вектору 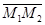 .
.
Решение.Вектор 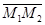 будет являться вектором нормали плоскости, его координаты равны
будет являться вектором нормали плоскости, его координаты равны 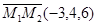 . Теперь вос-пользуемся уравнением (8):
. Теперь вос-пользуемся уравнением (8): 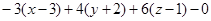
или 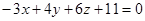
Пусть заданы три точки
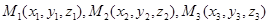 .Надо составить уравнение плоскости, проходящей через заданные точки. Для этого возьмем произвольную точку
.Надо составить уравнение плоскости, проходящей через заданные точки. Для этого возьмем произвольную точку 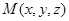 этой плоскости, тогда векторы
этой плоскости, тогда векторы 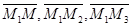 лежат в данной плоскости, то есть компланарны. Следовательно, их смешанное произведе-ние равно нулю
лежат в данной плоскости, то есть компланарны. Следовательно, их смешанное произведе-ние равно нулю  или
или
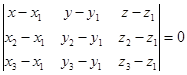 (9)
(9)
Уравнение (9) – это уравнение плоскости, проходящей через три заданные точки.