Прямая на плоскости.
Положение прямой на плоскости будет определено, если задать единичный вектор 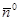 , перпендикулярный прямой и выходя-щий из начала координат, и расстояние то начала координат до прямой -
, перпендикулярный прямой и выходя-щий из начала координат, и расстояние то начала координат до прямой - 
 , (рис.4). Возьмем на прямой произволь-ную точку
, (рис.4). Возьмем на прямой произволь-ную точку  .
.

Рис.4
Когда точка движется по прямой, то ее радиус-вектор 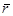 меня-ется так, что все время связан условием:
меня-ется так, что все время связан условием:  , оно выполняется для всех точек прямой, то есть это равенство выражает общее свойство точек прямой и только их. По свойству скалярного произведения
, оно выполняется для всех точек прямой, то есть это равенство выражает общее свойство точек прямой и только их. По свойству скалярного произведения
 , следовательно,
, следовательно,
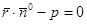 (11)
(11)
Это нормальное уравнение прямой в векторной форме. Так как 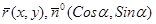 , подставляем в уравнение (11) и полу-чим нормальное уравнение прямой в координатной форме:
, подставляем в уравнение (11) и полу-чим нормальное уравнение прямой в координатной форме:
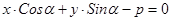 (12)
(12)
Утверждение 2.Любое уравнение первой степени с двумя пере-менными определяет прямую на плоскости.
Доказательство. Рассмотрим линейное уравнение первой сте-пени с двумя переменными
 (13)
(13)
Коэффициенты  и
и  будем рассматривать как проекции на оси координат некоторого постоянного вектора
будем рассматривать как проекции на оси координат некоторого постоянного вектора  , а
, а  и
и  - как проекции радиус-вектора
- как проекции радиус-вектора 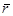 точки
точки  . Запишем это урав-нение в векторной форме:
. Запишем это урав-нение в векторной форме:
 (14)
(14)
Рассмотрим три случая:
1. пусть 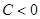 , разделим (14) на
, разделим (14) на , получим
, получим
 , где
, где  , обозначим
, обозначим 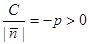 , тогда уравнение (14) примет вид
, тогда уравнение (14) примет вид
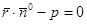
2. пусть 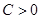 , разделим (13) на
, разделим (13) на 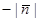 , получим
, получим
 , где
, где  .
.
3. пусть 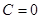 , разделим (13) на
, разделим (13) на  или
или 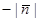 , тогда получим
, тогда получим
 или
или 
Каждое из полученных в трех случаях уравнений вида (11). То есть уравнение вида (13) можно привести к уравнению (11), а это значит, что уравнение (13) определяет прямую на плоскости.
Уравнение (13) называется общим уравнением прямой на плоскости.
Определение 2.Любой ненулевой вектор, перпендикулярный прямой, называется вектором нормали.
Векторов нормали для прямой бесконечно много, все они колли-неарны между собой, коэффициенты при переменных в общем уравнении прямой – это координаты одного из векторов норма-ли, то есть  - один из векторов нормали.
- один из векторов нормали.
Чтобы привести общее уравнение прямой на плоскости к нормальному уравнению, нужно воспользоваться нормирую-щим множителем:
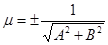 (15)
(15)
знак берется противоположным знаку 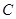 ( если
( если 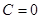 , то знак берется произвольно). Умножаем уравнение (13) на нормирую-
, то знак берется произвольно). Умножаем уравнение (13) на нормирую-
щий множитель, получим: 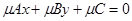 или
или  , где
, где
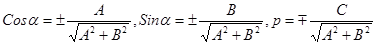
верхние знаки берутся, если  нижние – в противополож-ном случае.
нижние – в противополож-ном случае.