Частные случаи расположения прямой на плоскости.
Рассмотрим общее уравнение прямой на плоскости (13):
1.Если 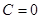 , тогда уравнение (13) примет вид
, тогда уравнение (13) примет вид 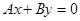 . Координаты точки
. Координаты точки  удовлетворяют этому уравнению, следовательно, в этом случае прямая проходит через начало координат.
удовлетворяют этому уравнению, следовательно, в этом случае прямая проходит через начало координат.
2. Если 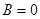 , то уравнение (13) примет вид
, то уравнение (13) примет вид  или
или  , то есть прямая параллельна оси ординат.
, то есть прямая параллельна оси ординат.
3. Если 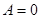 , то получим уравнение
, то получим уравнение 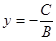 , в этом случае прямая параллельна оси абсцисс.
, в этом случае прямая параллельна оси абсцисс.
4. Если  , то получим уравнение
, то получим уравнение 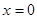 - это уравнение оси
- это уравнение оси 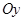 .
.
5. Если  , то уравнение
, то уравнение 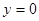 определяет ось
определяет ось 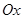 .
.
Пусть прямая не параллельна ни одной оси и даны точки пере-сечения прямой с осями координат  (рис.5):
(рис.5):

Рис.5
Составим по этим данным уравнение прямой. Воспользуемся общим уравнением прямой на плоскости (13), в этом уравнении нужно найти коэффициенты 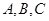 , для этого подставим
, для этого подставим
координаты точек  и
и 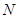 в уравнение, получим:
в уравнение, получим: 
следовательно, , подставляем найденные коэффициенты в (41), получаем
, подставляем найденные коэффициенты в (41), получаем 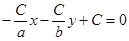 или
или  , разделим это уравнение на
, разделим это уравнение на 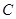 , получим урав-нение прямой в отрезках:
, получим урав-нение прямой в отрезках:
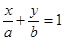 (16)
(16)
числа 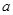 и
и  показывают, какие отрезки на осях координат отсекает данная прямая.
показывают, какие отрезки на осях координат отсекает данная прямая.
Пример 3.Составить уравнение прямой, проходящей через точку 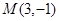 и отсекающей на осях координат равные отрезки.
и отсекающей на осях координат равные отрезки.
Решение.Так как прямая отсекает на осях координат равные отрезки, то  , воспользуемся уравнением (16), подставим координаты точки
, воспользуемся уравнением (16), подставим координаты точки  в это уравнение, получим
в это уравнение, получим
 , тогда
, тогда  , подставляем в (16), получаем
, подставляем в (16), получаем
 или
или 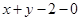 .
.
Определение 3.Вектор, параллельный данной прямой или лежащий на этой прямой, назывется направляющим вектором прямой.

Рис.6
Пусть  - направляющий вектор прямой.
- направляющий вектор прямой.
Определение 4.Угловым коэффициентом прямой называется отношение проекции направляющего вектора на ось ординат к его проекции на ось абсцисс.
 (17)
(17)
Пусть задан угловой коэффициент прямой  и точка пересе-чения прямой с осью
и точка пересе-чения прямой с осью 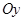
 . Составим уравнение этой прямой.
. Составим уравнение этой прямой.
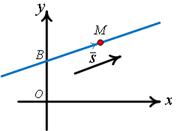
| |
Рис.7
Возьмем произвольную точку  на прямой (рис.7), тогда вектор
на прямой (рис.7), тогда вектор  будет направляющим, следовательно,
будет направляющим, следовательно,  , выразив из этого соотношения
, выразив из этого соотношения  , получим уравнение прямой с угловым коэффициентом:
, получим уравнение прямой с угловым коэффициентом:
 (18)
(18)
Пусть задана точка  через которую проходит прямая и угловой коэффициент этой прямой
через которую проходит прямая и угловой коэффициент этой прямой  . Надо составить урав-нение этой прямой. Для этого воспользуемся уравнением (18), в котором требуется найти коэффициент
. Надо составить урав-нение этой прямой. Для этого воспользуемся уравнением (18), в котором требуется найти коэффициент  . Подставим в уравне-ние (18) координаты точки
. Подставим в уравне-ние (18) координаты точки 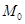 , получим
, получим  , вычитая из (18) данное равенство, получим:
, вычитая из (18) данное равенство, получим:
 (19)
(19)
это уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом.
Если в уравнении (19) угловой коэффициент  будет прини-мать всевозможные значения, то это уравнение будет опреде-лять пучок прямых с центром в точке
будет прини-мать всевозможные значения, то это уравнение будет опреде-лять пучок прямых с центром в точке 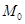 .
.
Пусть задана точка  , через которую проходит прямая, и направляющий вектор прямой
, через которую проходит прямая, и направляющий вектор прямой . Составим уравнение этой прямой, воспользовавшись уравнением (19):
. Составим уравнение этой прямой, воспользовавшись уравнением (19):
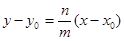
преобразовав это равенство, получим каноническое уравнение прямой:
 (20)
(20)
Уравнение (20) можно рассматривать как пропорцию, поэтому  , отсюда получаем:
, отсюда получаем:
 (21)
(21)
это параметрические уравнения прямой на плоскости.
Пусть даны две точки  , через которые проходит прямая. Составим уравнение данное прямой. Воспользуемся каноническим уравнением прямой (20), в качестве направляющего вектора возьмем вектор
, через которые проходит прямая. Составим уравнение данное прямой. Воспользуемся каноническим уравнением прямой (20), в качестве направляющего вектора возьмем вектор  :
:
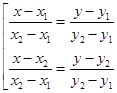 (22)
(22)
Оба уравнения являются уравнениями прямой, проходящей через две заданные точки.
Определение 5.Углом между прямыми на плоскости называ-ется любой из двух смежных углов, образованных этими пря-мыми( если прямые параллельны, то угол между ними 0 или  ).
).
Расстояние от точки  до прямой (13) находится
до прямой (13) находится
аналогично расстоянию от точки до плоскости:
 (23)
(23)