Прямая в пространстве.
Прямая в пространстве может быть получена в результате пересечения двух плоскостей, то есть задана аналитически системой двух уравнений первой степени с тремя переменными.
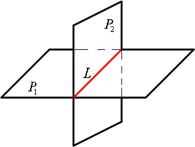
Рис.9

L: 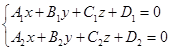 (25)
(25)
Уравнения (25) называются общими уравнениями прямой в пространстве.
Положение прямой в пространстве определено, если задана точка 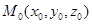 , через которую проходит прямая, и направ-
, через которую проходит прямая, и направ-
| |
 .
.
| |

Рис.10
Возьмем произвольную точку на прямой 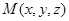 , векторы
, векторы 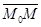 и
и 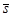 коллинеарны, то есть
коллинеарны, то есть 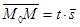 , если направле-ния векторов совпадают, то
, если направле-ния векторов совпадают, то  , в противном случае
, в противном случае  .
.
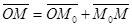
так как 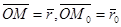 , то
, то
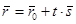 (26)
(26)
это векторное уравнение прямой в пространстве, переходя от векторного уравнения к координатным уравнениям, получим
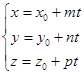 (27)
(27)
это параметрические уравнения прямой в пространстве, 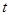 - параметр. Если исключить из уравнений (27) параметр, получим канонические уравнения прямой в пространстве
- параметр. Если исключить из уравнений (27) параметр, получим канонические уравнения прямой в пространстве
 (28)
(28)
Как перейти от общих уравнений прямой к каноническим?
1. Надо из системы (25) найти координаты точки, через которую проходит прямая. Так как система содержит два уравнения, а пе-ременных три, одну из переменных нужно задать произвольным образом, например, 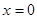 , а две другие найти из системы.
, а две другие найти из системы.
2. Так как прямая лежит и в одной, и в другой плоскости, то век-торы нормали этих плоскостей перпендикулярны направляю-щему вектору прямой, следовательно, 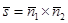 , тогда
, тогда

Пример 4.Даны общие уравнения прямой  . Составить канонические уравнения этой прямой.
. Составить канонические уравнения этой прямой.
Решение.Найдем точку, через которую проходит данная прямая, для этого в системе положим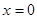 , тогда решая сис-тему, получим
, тогда решая сис-тему, получим  . Теперь найдем координаты направляющего вектора:
. Теперь найдем координаты направляющего вектора: 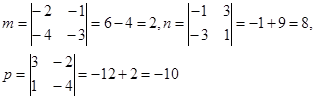 ,
,
составляем канонические уравнения прямой:
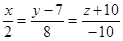 .
.
Дана точка  и прямая
и прямая 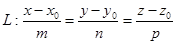 . Надо найти расстояние от точки
. Надо найти расстояние от точки
до прямой.
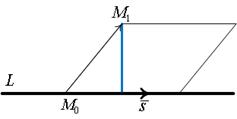
| |

Искомое расстояние – это высота параллелограмма, построен-ного на векторах  и
и 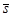 . Найдем площадь параллело-грамма
. Найдем площадь параллело-грамма  тогда
тогда
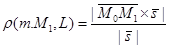 (29)
(29)