Элементарными преобразованиями матрицы. Метод Крамера. Определение вектора

1.1 Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3, . . . , n в строчку одно за другим.

Два элемента перестановки образуют инверсию, если в записи перестановки больший элемент предшествует меньшему.

1.2 Существует n! различных перестановок n-ой степени из n чисел. Докажем эту теорему. Рассмотрим n различных чисел a1,a2,a3, . . . ,an. На первое место перестановки существует n способов выбора записи чисел; на второе место остаётся уже (n-1) способ выбора чисел; на третье место останется (n-2) варианта выбора и т.д., а на последнее место остаётся один единственный вариант. Тогда можем записать, что число всех перестановок n-ой степени из n элементов равно: n·(n-1)·(n-2)· . . . ·2·1=n!. Символ n! читается ЭН- факториал. Таким образом, n! означает произведение всех натуральных чисел, не превосходящих данного числа. Теорема доказана.

2.1 Перестановка называется чётной, если общее количество инверсий есть чётное число и, соответственно, нечётной, если общее количество инверсий, содержащихся в этой перестановке , число нечётное.

Транспозицией называется такое преобразование перестановки, при котором какие – либо два её элемента меняются местами, а все остальные элементы остаются на своих местах.

2.2Все n! перестановок можно записать в таком порядке, что каждая следующая будет получаться из предыдущей с помощью одной транспозиции (такой порядок называется идеальным), при этом ни одна перестановка не встретится дважды, а начинать можно с любой перестановки. Следствие из теоремы : из какой–либо перестановки n-ой степени можно получить любую другую перестановку n-ой степени с помощью нескольких транспозиций.

Любая транспозиция меняет чётность перестановки на противоположную.

3.1Подстановкой n-ой степени называется любое отображение множества натуральных чисел от 1 до n самого на себя. Каждую подстановку будем записывать в две строки, предполагая, что под каждым числом записано именно то число, которое ему соответствует. Заметим, что порядок чисел в верхней строчке является несущественным, например, рассмотрим подстановку пятой степени:

 

3 2 5 1 4 5 3 1 4 2

2 4 1 5 3 1 2 5 3 4

 

Здесь и в той и в другой подстановке 1 переходит в 5; 2 переходит в 4; 3 переходит в 2; 4 переходит в 3 и 5 переходит в 1. Поэтому эти подстановки тождественные. Каждую подстановку можно записывать так, чтобы все числа в первой строке располагались в порядке возрастания. При такой записи подстановок любые две подстановки одной степени будут отличаться только перестановками во второй строке. Отсюда следует довольно простой и важный вывод: существует n! различных подстановок n – ой степени.

3.2. Будем называть подстановку чётной, если общее количество инверсий, содержащихся и впервой и во второй строчках чётное число и нечётной, если общее число инверсий в двух строчках – число нечётное.

4.1Система из m·n чисел, записанная в вид таблицы из m строк и n столбцов, называется числовой матрицей. В случае, когда m=n матрица называется квадратной.

4.2 Определителем порядка n, или детерминантом квадратной матрицы, называется алгебраическая сумма из n! слагаемых, каждое из которых представляет собой произведение n элементов нашей матрицы, взятых каждый раз по одному из каждой строчки и из каждого столбца, при этом слагаемые берутся со знаком (+), если индексы его сомножителей образуют чётную подстановку, и со знаком (-) , если его индексы образуют нечётную подстановку. По поводу второго вопроса в этом разделе – рисуем чертеж, где объясним правило треугольника. А для определителя второго порядка вообще все просто.

5.1Смотри 4.2

5.2При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится. Если две строки (столбца) матрицы совпадают, то её определитель равен нулю. Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю. Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1). Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя. Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю. Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю. Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю. Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей.

6.1Алгебраическим дополнением элемента 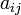матрицы называется число ,

где 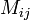— дополнительный минор, определитель матрицы, получающейся из исходной матрицы путем вычёркивания i -й строки и j -го столбца.

6.2 Теорема Лапласа. Величина определителя равна сумме произведений элементов строки определителя на их алгебраические дополнения. Пусть выбраны любые 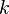строк матрицы . Тогда определитель матрицы равен сумме всевозможных произведений миноров 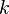-го порядка, расположенных в этих строках, на их алгебраические дополнения.

где суммирование ведётся по всевозможным номерам столбцов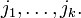

Широко известен частный случай теоремы Лапласа — разложение определителя по строке или столбцу. Он позволяет представить определитель квадратной матрицы в виде суммы произведений элементов любой её строки или столбца на их алгебраические дополнения. Пусть — квадратная матрица размера . Пусть также задан некоторый номер строки 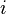либо номер столбца 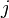матрицы .

7.1 Думаю сами сможете объяснить на примерах. Ничего трудного нет. Свойства из 7.2 могут помочь.

7.2 Свойства умножения матриц на число:

1. 1A = A;

2. (λβ)A = λ(βA)

3. (λ+β)A = λA + βA

4. λ(A+B) = λA + λB

Свойства сложения матриц:

1.коммутативность: A+B = B+A;

2.ассоциативность: (A+B)+C =A+(B+C);

3.сложение с нулевой матрицей: A + Θ = A;

4.существование противоположной матрицы: A + (-A) = Θ;

Умножение матриц (обозначение: , реже со знаком умножения ) — есть операция вычисления матрицы , каждый элемент которой равен сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

Количество столбцов в матрице должно совпадать с количеством строк в матрице , иными словами, матрица обязана быть согласованной с матрицей . Если матрица имеет размерность , — , то размерность их произведения есть .

Свойства умножения матриц:

1. Ассоциативность (AB)C = A(BC);

2. Некоммутативность (в общем случае): AB BA;

3. Произведение коммутативно в случае умножения с единичной матрицей: AI = IA;

4. Дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC;

5. Ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB);

Умножение матриц (обозначение: , реже со знаком умножения ) — есть операция вычисления матрицы 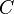, каждый элемент которой равен сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

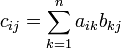
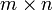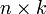Количество столбцов в матрице должно совпадать с количеством строк в матрице , иными словами, матрица обязана быть согласованной с матрицей . Если матрица имеет размерность , — , то размерность их произведения есть .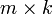

Свойства умножения матриц:

Свойства умножения матриц на число:

1. 1A = A;

2. (λβ)A = λ(βA)

3. (λ+β)A = λA + βA

4. λ(A+B) = λA + λB

Свойства сложения матриц:

1. Коммутативность: A+B = B+A;

2. Ассоциативность: (A+B)+C =A+(B+C);

3. Сложение с нулевой матрицей: A + Θ = A;

4. Существование противоположной матрицы: A + (-A) = Θ;

Умножение матриц (обозначение: , реже со знаком умножения ) — есть операция вычисления матрицы , каждый элемент которой равен сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

Количество столбцов в матрице должно совпадать с количеством строк в матрице , иными словами, матрица обязана быть согласованной с матрицей . Если матрица имеет размерность , — , то размерность их произведения есть .

Свойства умножения матриц:

1. Ассоциативность (AB)C = A(BC);

2. Некоммутативность (в общем случае): AB BA;

3. Произведение коммутативно в случае умножения с единичной матрицей: AI = IA;

4. Дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC;

5. Ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB);

8.1 Транспонированная матрица — матрица , полученная из исходной матрицы заменой строк на столбцы. Формально, транспонированная матрица для матрицы размеров 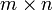—матрица размеров , определённая как A^T[i, j] = A[j, i].

8.2 Дважды транспонированная матрица А равна исходной матрице А.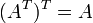

Транспонированная сумма матриц равна сумме транспонированных матриц. Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке.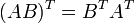

При транспонировании можно выносить скаляр.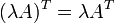

Определитель транспонированной матрицы равен определителю исходной матрицы.

9. 1).Определитель произведения двух квадратных матриц равен произведению определителей этих матриц.

Определитель произведения двух квадратных матриц одинакового порядка равен произведению определителей этих матриц.

2).Теорема об определителе произведения квадратных матриц.

Теорема. Определитель произведения квадратных матриц равен произведению

определителей этих матриц.

Теорему можно записать в виде формулы: lABl = lAl lBl.

10. 1). Диагональная матрица, все диагональные элементы которой равны единице (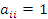), называется единичной матрицей и обозначается символом E. Обратная матрица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E: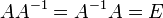

2).

3). Теорема (единственности существования обратной матрицы): Если у матрицы существует обратная матрица , то она единственна.

Доказательство.

Пусть существует матрица 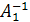, для которой 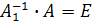и матрица , для которой .

Тогда , то есть 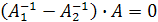. Умножим обе части равенства на матрицу 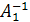, получим 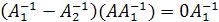, где и .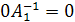

Значит, , что и требовалось доказать.

11.1). Обратная матрица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E: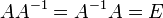

2). С помощью присоединенной матрицы (практически не применяемый метод).

Задача:

Дана матрица 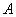. Требуется вычислить обратную к ней матрицу .

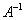Алгоритм решения:

Записать исходную матрицу с присоединенной к ней единичной.

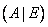
2) Алгебраическими преобразованиями, проводимыми со строками полученной составной матрицы приводим ее к такому виду, чтобы в левой половине стояла единичная матрица. Тогда в правой половине будет стоять матрица .

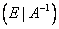
3)Проверка.

 

12.1).Элементарными преобразованиями матрицы называются преобразования следующих трёх типов:

1) Перестановка двух строк (столбцов) матрицы;

2) Умножение строки (столбца) на число отличное от нуля;

3) Прибавление к одной строке (столбцу) матрицы другой её строки (столбца), умноженной на любое число.

2).Ступенчатой называется матрица, удовлетворяющая следующим условиям:

если эта матрица содержит нулевую строку (т.е. строку, все элементы которой равны нулю), то все строки, расположенные под нею, также нулевые;

если первый ненулевой элемент некоторой строки расположен в столбце с номером , то первый ненулевой элемент следующей строки должен находиться в столбце с номером большим, чем .

 

Теорема. Любая матрица может быть приведена к ступенчатой матрице при помощи элементарных преобразований первого и второго типов.

Пример. Привести матрицу A к ступенчатому виду при помощи элементарных преобразований первого и второго типов.

 

 

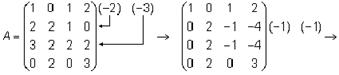
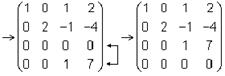
3).

Предположим, что матрица A - неособенная и рассмотрим метод нахождения обратной матрицы, основанный на элементарных операциях над строками.

В данном контексте под элементарными преобразованиями понимается:

Умножение строки на любое ненулевое число.

Прибавление к одной строке любой другой, предварительно умноженной на любое число.

Алгоритм метода чрезвычайно прост по своей сути.

Сначала составляется расширенная матрица – присоединением к матрице A единичной матрицы E

Затем с помощью элементарных операций над строками расширенная матрица (A | E) преобразуется к виду (E | B).

С формальной точки зрения такие преобразования могут быть реализованы умножением на матрицу A некоторой матрицы T, которая представляет собой произведение соответствующих элементарных матриц (матрицы перестановки, матрицы масштабирования, неунитарной матрицы):

TA = E.

Это уравнение означает, что матрица преобразования T представляет собой обратную матрицу для матрицы A:

T = A-1.

13.1 Определение. Система линейных уравнений — это объединение из nлинейных уравнений, каждое из которых содержит k переменных. Записывается это так:

Определение. Решение системы уравнений — это последовательность чисел (k₁, k₂, ..., k_n), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x₁,x₂, ..., x_n дает верное числовое равенство.

Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:

Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.

Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.

Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество.

13.2 Решим систему уравнений

 

	3 x1	- x2		=
-2 x1	+ x2	+ x3	=
2 x1	- x2	+ 4 x3	=

 

Запишем систему уравнений в матричной форме

 

A * X = B

 

-   *   -     -

x1   =     x2       x3

 

Найдем матицу A-1, обратную к матрице А, методом алгебраических дополнений. Осталось, только записать обратную матрицу.   A -1 = 1 / 5 *   -       -     A -1 =   -         -       Вернемся к нашему уравнению, которое мы записали в матричной форме.   A * X = B   Умножим левую и правую часть нашего матричного уравнения на A-1   A-1 * A * X = A-1 * B       -     *   -         -   *   -     -         x1   =     x2       x3       -     *   -       Произведение обратной матрицы на исходную есть единичная матрица, т.е. A-1 * A = Е, следовательно   X = A-1 * B         x1   =     x2       x3       -     *   -       x1 = * + * + ( - )   * = + + ( - ) =   x2 = * + * + ( - )   * = + + ( - ) =   x3 = * + * + * = + + =   Ответ :   x1 = 2   x2 = 1   x3 = 3

14.1Смотри 13.2.

14.2Метод Крамера состоит в том, что мы последовательно находим главный определитель системы (5.3), т.е. определитель матрицы А

D = det (a_{i j})

и n вспомогательных определителей D _i (i=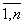), которые получаются из определителя D заменой i-го столбца столбцом свободных членов.

Формулы Крамера имеют вид:

D × x _i = D _i ( i = ).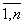

Из (5.4) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы (5.3): если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам:

x _i = D _i / D.

Если главный определитель системы D и все вспомогательные определители D _i = 0 (i= 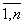), то система имеет бесчисленное множество решений. Если главный определитель системы D = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.

15.1 Определение. Две системы линейных уравнений называютсяравносильными, если множество всех их решений совпадает.

Определение. Элементарные преобразования системы уравнений — это:

Вычеркивание из системы тривиальных уравнений, т.е. таких, у которых все коэффициенты равны нулю;

Умножение любого уравнения на число, отличное от нуля;

Прибавление к любому i-му уравнению любого j-то уравнения, умноженного на любое число.

Определение. Переменная x_i называется свободной, если эта переменная не является разрешенной, а вся система уравнений — является разрешенной.

Теорема. Элементарные преобразования переводят систему уравнений в равносильную.

Смысл метода Гаусса заключается в том, чтобы преобразовать исходную систему уравнений и получить равносильную разрешенную или равносильную несовместную систему.

Итак, метод Гаусса состоит из следующих шагов:

Рассмотрим первое уравнение. Выберем первый ненулевой коэффициент и разделим все уравнение на него. Получим уравнение, в которое некоторая переменная x_i входит с коэффициентом 1;

Вычтем это уравнение из всех остальных, умножая его на такие числа, чтобы коэффициенты при переменной x_i в остальных уравнениях обнулились. Получим систему, разрешенную относительно переменной x_i, и равносильную исходной;

Если возникают тривиальные уравнения (редко, но бывает; например, 0 = 0), вычеркиваем их из системы. В результате уравнений становится на одно меньше;

Повторяем предыдущие шаги не более n раз, где n — число уравнений в системе. Каждый раз выбираем для «обработки» новую переменную. Если возникают противоречивые уравнения (например, 0 = 8), система несовместна.

В результате через несколько шагов получим либо разрешенную систему (возможно, со свободными переменными), либо несовместную. Разрешенные системы распадаются на два случая:

Число переменных равно числу уравнений. Значит, система определена;

Число переменных больше числа уравнений. Собираем все свободные переменные справа — получаем формулы для разрешенных переменных. Эти формулы так и записываются в ответ.

15.2ХЗ

16 Определение вектора

Вектором называется упорядоченное множество из 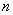элементов поля, обозначаемое как . Величины называются компонентами (координатами) вектора. Число компонентов вектора 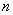называется длиной вектора. Векторы считаются равными, если равны их соответствующие компоненты. Число ненулевых компонентов вектора называют весом вектора [33].

Сложение двух векторов длины 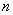определяется следующим образом:

.

Умножение элемента поля на вектор производится покомпонентно:

,

причем сложение и умножение компонентов векторов происходит по правилам сложения и умножения в поле .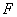

Для векторов введено понятие нормы [25, 33], которая для вектора 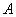определяется как 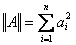, где символ означает суммирование в поле действительных чисел. Если компоненты вектора принадлежат двоичному полю, то норма вектора совпадает с числом его ненулевых компонентов, т.е. с его весом.

Вектор 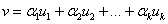, где – элементы поля, называют линейной комбинацией векторов . Векторы называются линейно зависимыми, если в 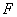существуют такие элементы , по крайней мере один из которых не равен нулю, такие что 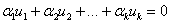и линейно независимыми в противном случае. Если векторы линейно зависимы, то любой из них может быть выражен через линейную комбинацию остальных.

Определение векторного пространства

Множество 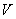называется векторным пространством, если для него выполняются следующие аксиомы:

V. 1. Множество 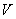является аддитивной абелевой группой.

V.2. Для любого вектора 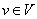и любого скаляра – элемента 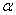поля 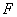определено произведение 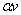, являющееся вектором. Это произведение определено так, что 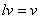, где 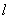– единичный элемент поля .

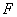V.3. Выполняются законы дистрибутивност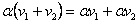и

и ,

где 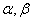– скаляры, а и – векторы.

V.4. Выполняется закон ассоциативности

,

где 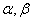– скаляры, а – вектор.

 

Свойства векторного пространства

1. Максимальное число линейно независимых векторов в 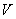называется размерностью пространства 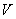над полем .

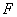2. Совокупность 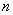любых линейно независимых векторов называется базисом и-мерного пространства, если каждый из векторов пространства может быть представлен в виде линейной комбинации этих векторов. Векторы совокупности называются базисными.

3. Подмножество векторного пространства 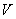такое, что любая линейная комбинация векторов этого подмножества снова принадлежит , называется подпространством пространства 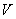. Легко проверить, что все векторы подпространства удовлетворяют аксиомам V.1 – V.4. Очевидно, что размерность подпространства не превышает размерности пространства, т.к. во всем пространстве содержится не более 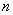линейно независимых векторов. Каждое подпространство можно рассматривать как самостоятельное пространство. Следовательно, каждое подпространство имеет свой базис.

4. Скалярным произведением двух векторов одинаковой длины 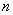: 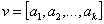и называется скаляр, определяемый как

.

Можно показать, что 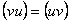и .

Если скалярное произведение двух векторов равно нулю, то говорят, что эти векторы ортогональны. Два пространства называются взаимно ортогональными, если каждый вектор одного пространства ортогонален любому вектору другого пространства.

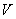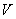Множество всех векторов пространства , ортогональных подпространству , образуют подпространство пространства . Подпространство часто называют нулевым пространством для .

Можно показать, что если – подпространство размерности 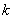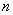-мерного векторного пространства 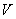, то размерность нулевого пространства равна .

5. Для векторного пространства определено понятие расстояния между двумя векторами, которое совпадает с нормой разности этих векторов

,

где суммирование производится в поле действительных чисел.

17.1 Система векторов e1,e2, ..., ek линейного пространства L называется линейно независимой системой, если равенство С1·e1+С2·e2+ ...+Сk· ek = 0 возможно только когда все коэффициенты С1, С2, ..., Сk равны нулю. Здесь 0 — нулевой вектор линейного пространства L, С1, С2, ..., Сk — числовые коэффициенты. Если система векторов e1,e2, ..., ek линейного пространства L не является линейно независимой системой, то она называется линейно зависимой системой векторов. Если это равенство выполняется только при ?1 = ?2 = … = ?n = 0 , то система векторов называется линейно независимой. Вместо "линейно зависимая (или независимая) система векторов" можно говорить просто "линейно зависимые (или независимые) векторы".

17.2 Для того, чтобы система векторов линейного пространства была линейно зависима, необходимо и достаточно, чтобы хотя бы один из векторов системы линейно выражался через остальные векторы системы (мог быть представлен в виде разложения по векторам системы).

18.1 Система векторов x1, x2, … , xn О X называется линейно зависимой, если существуют числа ?1, ?2, … , ?n О R , не все равные нулю (т.е. ?12 + ?22 + … + ?n2 ? 0 ), такие, что ?1x1 + ?2x2 + … + ?nxn = ?. Если это равенство выполняется только при ?1 = ?2 = … = ?n = 0 , то система векторов называется линейно независимой. Вместо "линейно зависимая (или независимая) система векторов" можно говорить просто "линейно зависимые (или независимые) векторы"., Любое непустое подмножество системы векторов называется подсистемой данной системы векторов.

18.2 Если система векторов содержит линейно зависимую подсистему, то сама система векторов тоже линейно зависима.

19.1

19.2 Система векторов называется максимальной линейно независимой системой, если она линейно независима и ее нельзя включить в большую линейно независимую систему в качестве подсистемы.

19.3 Все максимальные линейно независимые подсистемы данной системы векторов содержат одно и то же число векторов. Т2 Ранги эквивалентных систем векторов равны.

20.1 Рангом системы векторов называется максимальное число линейно независимых векторов системы.,То есть, если ранг матрицы равен r, то среди миноров матрицы порядка r есть хотя бы один, отличный от нуля, а все миноры матрицы более высоких порядков равны нулю., То есть, если ранг матрицы равен r, то среди миноров матрицы порядка r есть хотя бы один, отличный от нуля, а все миноры матрицы более высоких порядков равны нулю.

20.2Ранг матрицы А равен максимальному числу линейно независимых столбцов (или равен рангу системы столбцов матрицы А).

20.3 1).транспозиция любых ее двух строк или столбцов; 2).умножение любой строки (столбца) матрицы на число, отличное от нуля; 3). прибавление к любой строке (столбцу) матрицы другой строки (столб-ца), умноженной на число.

21.1 Ранг матрицы А равен максимальному числу линейно независимых столбцов (или равен рангу системы столбцов матрицы А)

21.2 Строки квадратной матрицы линейно зависимы тогда и только тогда, когда определитель этой матрицы равен нулю.

Теорема Кронекера-Капелли

Составим матрицу и расширенную матрицу: А=и =. Очевидно, что r(A)=r().

Число решений системы линейных уравнений в зависимости от числа неизвестных и рангов матрицы и расширенной матрицы системы.

Системы линейных уравнений совместные r(A)=r() несовместные r(A)≠r().

Понятие однородной системы линейных уравнений.

называется однородной системой линейных уравнений. Из теоремы Кронекера-Капелли следует, что указанная система всегда совместна,… При этом если ранг системы равен количеству неизвестных, то система имеет только нулевое решение.

Свойство решений однородной СЛУ.

x=и y=решения системы. и и

Фундаментальная система решений.

Из всех решений однородной системы уравнений можно выбрать максимально линейнонезависимую систему. Всякая максимально линейнонезависимая система решений называется фундаментальной системой решений (ФСР).

Если r(A)=r, то ФСР = n-r векторов.

Связь между решениями однородных и неоднородных систем линейных уравнений.

I и II Теорема. Сумма любого решения системы I с любым решением системы II снова есть… Теорема. Разность двух любых решений системы I есть решение системы II .

Аксиоматический подход к определению линейного пространства.

Линейным, векторным или афинным пространством называется множество V, если: 1. На V определена операция сложения, для которой выполняются аксиомы: А)

Примеры линейных пространств

Множество всех направленных отрезков, параллельных оси ординат на плоскости:

Проверим аксиомы:

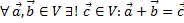
A)

Б):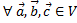

В)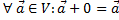

Г)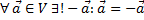

Д)

Е)

Ж)

З)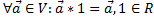

Вывод : множество всех направленных векторов на плоскости, параллельных оси OY, образует линейной пространство.

Следствия из аксиом.

2. Единственность противоположного вектора 3. Существование и единственность разности элементов 4. Произведение нулевого элемента на действительное число есть нулевой элемент.

Доказательство следствий

По аксиоме 1

Базис. Размерность. Координаты.

1) система линейно независима. 2) Любой элемент L линейно выражается через базисные (т.е. является линейной… Примеры. Базис на плоскости (V2 – 2 неколлинеарных вектора), в пространстве (V3 – 3 некомпланарных вектора), в…