Полные системы булевых функций
Полные системы функций  Править
Править
Множество 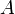 функций алгебры логики называется полной системой, если замыкание этого множества совпадает с множеством всех функций. (В частности, для двузначной логики
функций алгебры логики называется полной системой, если замыкание этого множества совпадает с множеством всех функций. (В частности, для двузначной логики 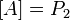 .) Другими словами, должна быть возможность любую функцию алгебры логики выразить формулой с использованием функций множества
.) Другими словами, должна быть возможность любую функцию алгебры логики выразить формулой с использованием функций множества 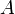 .
.
Критерий Поста формулирует необходимое и достаточное условие полноты системы булевых функций:
Система булевых функций полна тогда и только тогда, когда она не содержится целиком ни в одном из классов 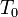 ,
, 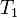 ,
, 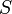 ,
, 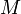 ,
, 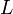 .
.
В частности, если функция не входит ни в один из классов Поста, она сама по себе формирует полную систему. В качестве примера можно назвать функцию Шеффера (отрицание конъюнкции).
Широко известны такие полные системы булевых функций:
§ 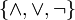 (конъюнкция, дизъюнкция, отрицание);
(конъюнкция, дизъюнкция, отрицание);
§ 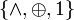 (конъюнкция, сложение по модулю 2, константа 1).
(конъюнкция, сложение по модулю 2, константа 1).
Первая система используется, например, для представления функций в виде дизъюнктивных иконъюнктивных нормальных форм, вторая - для представления в виде полиномов Жегалкина.
Полная система функций называется базисом, если она перестаёт быть полной при исключении из неё любого элемента. Первая из упоминавшихся выше полных систем базисом не является, поскольку согласнозаконам де Моргана либо дизъюнкцию, либо конъюнкцию можно исключить из системы и восстановить с помощью остальных двух функций. Вторая система является базисом — все три её элемента необходимы для полноты. Максимально возможное число булевых функций в базисе — 4.
Иногда говорят о системе функций, полной в некотором замкнутом классе, и соответственно о базисе этого класса. Например, систему 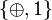 можно назвать базисом класса линейных функций.
можно назвать базисом класса линейных функций.
22.Алгебра Жегалкина
Множество булевых функций, заданный в базисе Жегалкина S4={⊕,&,1} называется алгеброй Жегалкина.
Основные свойства:
1. коммутативность: H1⊕H2=H2⊕H1; H1&H2=H2&H1.
2. ассоциативность: H1⊕(H2⊕H3)=(H1⊕H2)⊕H3; H1&(H2&H3)=(H1&H2)&H3.
3. дистрибутивность: H1&(H2⊕H3)=(H1&H2)⊕(H1&H3)
4. свойства констант: H&1=H; H&0=0; H⊕0=H.
5. H⊕H=0; H&H=H/
Утверждение. Через операции алгебры Жегалкина можно выразить все другие булевы функции:
¬X=1⊕X; XvY=X⊕Y⊕XY; X∼Y=1⊕X⊕Y; X→Y=1⊕X⊕XY; X↓Y=1⊕X⊕Y⊕XY; X|Y=1⊕XY Определение. Полиномом Жегалкина (полиномом по модулю 2) от n переменных X1,X2 ... Xn называется выражение вида: C0⊕C1X1⊕C2X2⊕ ... ⊕CnXn⊕C12X1X2⊕ ... ⊕C12 ... nX1X2 ... Xn,где постоянные Ck могут принимать значения 0 ли 1.