Представление произвольной логической функции в виде формулы алгебры логики

Пусть с помощью таблицы истинности задана произвольная функция алгебры логики n переменных F(x₁, x₂, …, x_n). Рассмотрим формулу:

F(1, 1, …, 1) Ù x₁ Ù x₂ Ù … Ù x_n Ú

Ú F(1, 1, …, 1, 0) Ù x₁ Ù x₂ Ù … Ù x_n-1 Ù Ø x_n Ú (1)

Ú F(1, 1, …, 0, 1) Ù x₁ Ù x₂ Ù … Ù Ø x_n-1 Ù x_n Ú

Ú F(0, 0, …, 0) Ù Ø x₁ Ù Ø x₂ Ù … Ù Ø x_n

которая составлена следующим образом: каждое слагае­мое этой логической суммы представляет собой конъюн­кцию, в которой первый член является значением функ­ции F при некоторых определенных значениях ее перемен­ных, остальные же члены конъюнкции пред­ставляют собой сами переменные или их отрицания. При этом под знаком отрицания находятся те и только те пере­менные, которые в первом члене конъюнкции имеют зна­чение 0.

Ясно, что формула (1) полностью определяет функ­цию F. Иначе говоря, значения функции F и формулы (1) совпадают на всех наборах значений пере­менных x_i. Например, если x₁ принимает значение 0, а осталь­ные переменные принимают значение 1, то функция F принимает значение F(0, 1, 1, …, 1). При этом логическое слагаемое F(0, 1, …, 1) Ù Ø x₁ Ù x₂ Ù … Ù x_n = F(0, 1, …, 1) Ù Ø 0 Ù 1 Ù … Ù 1, входящее в форму­лу (1), принимает также значение F(0, l,..., l), а все ос­тальные логические слагаемые формулы (1) имеют зна­чение 0. Действительно, в них знаки отрицания перед переменными распределяются иначе, чем в рассмотрен­ном слагаемом. Таким образом, при подстановке вместо переменных тех же значений в конъюнкцию войдет символ 0 без знака от­рицания, а символ 1 под знаком отрицания. В таком слу­чае один из членов конъюнкции будет иметь значение 0, и по­этому вся конъюнкция также будет иметь значение 0. В связи с этим на основании закона x Ú 0 = x значением фор­мулы (1) является F(0, l,..., l).

Ясно, что вид формулы (1) может быть значительно упрощен, если в ней отбросить те логические слагаемые, в которых первый член конъюнкции имеет значение 0 (и, следовательно, вся конъюнкция имеет значение 0). Если же в логическом слагаемом первый член конъюнк­ции (то есть определенное значение функции F) имеет значение 1, то, пользуясь законом 1 Ù х = x, этот член конъюнкции можно не выписывать.

Таким образом, в результате получается формула (1), которая содержит только элементарные переменные выс­казывания и обладает следующими свойствами:

• каждое логическое слагаемое формулы содержит все переменные, входящие в функцию F(x₁, x₂, …, x_n),
• все логические слагаемые формулы различны,
• ни одно логическое слагаемое формулы не содер­жит одновременно переменную и ее отрицание,
• ни одно логическое слагаемое формулы не содер­жит одну и ту же переменную дважды,

Перечисленные свойства будем называть свойства­ми совершенства или, коротко, свойствами. Из приведенных рассуждений видно, что каждой не тождественно ложной функции соответствует единствен­ная формула указанного вида.

Если функция F(x₁, x₂, …, x_n) задана таблицей ис­тинности, то соответствующая ей формула алгебры ло­гики может быть получена просто. Действительно, для каждого набора значений переменных, на котором фун­кция F(x₁, x₂, …, x_n) принимает значение 1, записывается конъюнкция элементарных переменных высказываний, взяв за член конъюнкции х_k, если значение x_k на ука­занном наборе значений переменных фун­кции F есть 1 и Ø х, если значение x_k есть 0. Дизъюнкция всех записан­ных конъюнкций и будет искомой формулой.

9. Двойственные функции

Определение. Функция 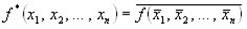называется двойственной к функции .

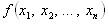Из определения следует, что для того, чтобы получить таблицу значений двойственной функции 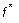, нужно в таблице значений функции 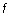(и в части переменных, и в части значений ) заменить все 0 на 1, а все 1 на 0. При этом, правда, порядок следования бинарных наборов 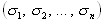в левой части таблицы изменится на обратный по сравнению с исходной таблицей. Чтобы его восстановить, нужно перевернуть все столбцы (в том числе и столбец значений). Таким образом, можно сформулировать следующее правило получения таблицы истинности двойственной функции 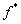: нужно (не меняя столбцы аргументов) в столбце значений функции 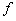заменить все 0 на 1, а 1 на 0, и перевернуть полученный столбец.

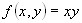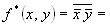
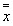
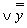
Пример. Пусть , тогда 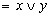. Таким образом, двойственной функцией к конъюнкции является дизъюнкция. Поскольку для всех функций очевидно 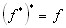, то обратно: двойственной к дизъюнкции является конъюнкция. Кроме того, легко видеть, что , ; , ; .

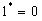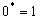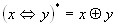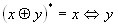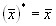Теорема: Функция, двойственная к суперпозиции функций, есть суперпозиции функций, двойственных к функциям, составляющим эту суперпозицию.

Доказательство:

(f(g1,…,gm))* = ¬f(g1(¬x1,1, ¬x1,2,…,¬x1,n1),…,gm(¬xm,1, ¬xm2,1,…,¬xm,nm)) =

=¬f(¬¬g1(¬x1,1,¬x2,1,…,¬x1,n1),…,¬¬gm(¬xm,1,¬xm,2,…,¬xm,nm))=¬f(¬g1*,…,¬gm*)=f*(g1*,…,gm*)