Свойства.
1) 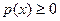
2) 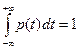
3) 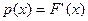 для почти всех x
для почти всех x
4) 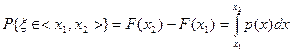
Пример 1:Плотность распределения случайной величины Z имеетвид 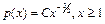 . Требуется найти: a) постоянную C; b) функцию распределения Z; с)
. Требуется найти: a) постоянную C; b) функцию распределения Z; с) 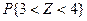 .
.
Решение:
a) Воспользуемся свойством (2). Имеем 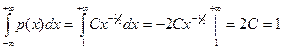 . Получаем С=0,5.
. Получаем С=0,5.
b) Согласно определению 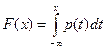 . Таким образом,
. Таким образом,
если 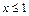 , то
, то 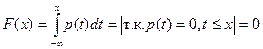
если x>1, то 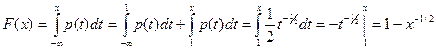
c) 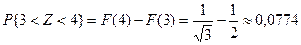
Пример 2.Найти плотность распределения с.в. 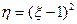 , если ξ имеет равномерное распределение на отрезке [-1,1].
, если ξ имеет равномерное распределение на отрезке [-1,1].
Решение.Обозначим функцию распределения с.в. η как G(x), а плотность распределения – g(x)=G’(x). Согласно определению 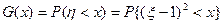 . Очевидно, что при x≤0 G(x) = 0. Если x>0, то
. Очевидно, что при x≤0 G(x) = 0. Если x>0, то 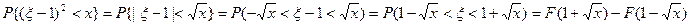 , где F(x) – функция равномерного распределения на [-1,1], т.е.
, где F(x) – функция равномерного распределения на [-1,1], т.е.
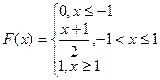
Таким образом 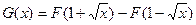 . Переходя к производной имеем
. Переходя к производной имеем
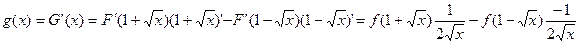 ,
,
где f(x)=F’(x) – плотность распределения с.в. ξ, т.е. 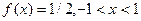 . Так как
. Так как 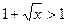 и следовательно
и следовательно 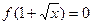 , то
, то 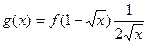 . Рассмотрим возможные варианты:
. Рассмотрим возможные варианты:
а) Если 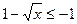 , то
, то 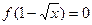 . Следовательно g(x)=0 при x≥4
. Следовательно g(x)=0 при x≥4
б) если 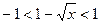 , то
, то 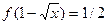 . Следовательно
. Следовательно 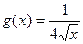 при 0<x<4
при 0<x<4
в) невозможно, чтобы 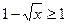
Медиана распределения Me.Для непрерывной случайной величины ξ с функцией распределения F(x) медианой распределения Me называется следующая величина: 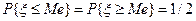 , т.е. F(Me)=0,5
, т.е. F(Me)=0,5
Мода распределения Mo называется точка максимума плотности распределения, если она существует.
Математическое ожиданиенепрерывной случайной величины ξ с плотностью распределения p(x)
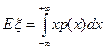 , если интеграл сходится
, если интеграл сходится