Коли рекурсію використовувати не потрібно

 

Рекурсивні алгоритми особливо підходять для задач, де оброблювані дані визначаються в термінах рекурсії. Однак це не означає, що таке рекурсивне визначення даних гарантує безперечність уживання для рішення задачі рекурсивного алгоритму. Фактично пояснення концепцій рекурсивних алгоритмів на невідповідних для цього прикладах і викликало широко розповсюджене упередження проти використання рекурсій у програмуванні; їх навіть зробили синонімом неефективності.

Програми, у яких варто уникати алгоритмічної рекурсії, можна охарактеризувати деякою схемою, що відображає їх побудову (специфічно, що тут є єдине звертання до Р в кінці або на початку всієї конструкції): P ≡ if В then S; P

або P ≡ S; if В then P (1)

Такі схеми природні в ситуаціях, коли обчислюються значення, що визначаються за допомогою простих рекурентних відносин.

Візьмемо добре відомий приклад обчислення факторіала числа n, коли для переходу до наступного числа послідовності потрібно виконати такі обчислення:

I:=I+1; F:=F*I

і тоді обчислення можуть бути виконані так:

WHILE I<n DO begin

I:=I+1; F:=I*F

end;

Узагалі ж програми, що побудовані по схемах (1), потрібно переписувати, керуючись схемою:

Р ≡[ х := х₀; WHILE У DO S ].

Звичайно, існують і більш складні схеми рекурсій, які можна і необхідно переводити в ітеративну форму.

Візьмемо як приклад обчислення чисел Фібоначчи, що визначаються рекурсивним співвідношенням:

fib_n+1 = fib_n + fib_{n – 1} , для п > 0; fib₀=0; fib₁=1.

В програмному прикладі 6.2 показана рекурсивна функція обчислення чисел Фібоначчи.

{===== Програмний приклад 6.2 =====}

function fib(i : integer): integer;

begin if i=0 then fib:=0 else

if i=1 then fib:=1 else

Fib:=Fib(n – 1)+Fib(n – 2)

end;

ОбчисленняFib_n, шляхом звертання до Fib(n) приводить до рекурсивних активацій цієї функції. Як часто це відбувається? Кожне звертання з п > 1 приводить ще до двох звертань, тобто загальне число викликів росте экспоненційно На рис. 6.1 показано як збільшується кількість звертань коли визначається п’яте число Фібоначчи.

 

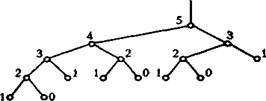
Рис. 6.1. Число звертань до Fib(5)

 

Ясно, що така програма практичного інтересу не має. Однак, числа Фібоначчи можна обчислювати і за ітеративною схемою, коли за допомогою допоміжних перемінних х = fib_i і y = fib_{i – 1} вдається уникнути повторних обчислень однієї і тієї ж величини (див. програмний приклад 6.3):

 

{===== Програмний приклад 6.3 =====}

function fib(n:integer):integer;

var

i,x,y,z: integer;

begin

і:= 1; x:= 1; y:= 0;

WHILE і<n DO

begin z:= х; х:= х + у;

у:= z; i:=i + 1;

end;

fib:= x;

end;

Отже, варто уникати рекурсій там, де є очевидне ітераційне рішення. Та це не означає, що рекурсій варто уникати за будь-яку ціну. Існує багато гарних прикладів застосування рекурсії. Те, що існують реалізації рекурсивних процедур на фактично не рекурсивних алгоритмах, доводить, що для практичних цілей будь-яку рекурсивну програму можна трансформувати в чисто ітеративну. Однак це вимагає явної роботи зі стеком для рекурсій, причому ці дії часто настільки затуманюють суть програми, що її буває важко зрозуміти.

Все сказане вище дозволяє зробити такий висновок: формулювати як рекурсивні процедури треба лише такі алгоритми, які рекурсивні по своїй природі, а не ітеративні.