Ответы и решения
Глава 2.
Ответы и решения.
Упражнение 1.1. Ответы: 1)  3) a) нет; б) да;
3) a) нет; б) да;
Упражнение 1.2.
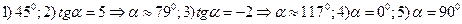
Упражнение 1.3.Решение 1). Выписываем формулу уравнения искомой прямой 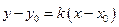 . По условию
. По условию  . Подставляя данные в формулу, получаем
. Подставляя данные в формулу, получаем .
.
2). По условию 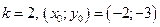 . Подставляя данные в формулу, получаем
. Подставляя данные в формулу, получаем .
.
3). Прямая горизонтальна, поэтому используем формулу (1.6) . Выписываем формулу уравнения прямой 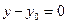 . Прямая проходит через точку
. Прямая проходит через точку  . Следовательно, её уравнение имеет вид
. Следовательно, её уравнение имеет вид 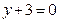 .
.
4). Прямая вертикальна, поэтому используем формулу (1.4). Выписываем формулу уравнения прямой . Прямая проходит через точку
. Прямая проходит через точку 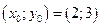 следовательно её уравнение имеет вид
следовательно её уравнение имеет вид  .
.
5). Вначале определяем угловой коэффициент прямой по формуле (1.1) . За начальную точку прямой
. За начальную точку прямой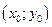 можно брать любую из точек
можно брать любую из точек уравнение от этого не изменится. Мы возьмём точку
уравнение от этого не изменится. Мы возьмём точку 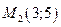 и подставим в формулу уравнения прямой
и подставим в формулу уравнения прямой  .
.
6)  .
.
7) 
Упражнение 1.3.
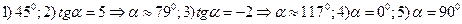
Упражнение 1.5. Найдём точку пересечения прямой  с осью ОХ. Ось ОХ прямая, имеющая уравнение
с осью ОХ. Ось ОХ прямая, имеющая уравнение 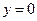 . Чтобы найти точку пересечения, решаем систему
. Чтобы найти точку пересечения, решаем систему

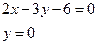
0твет:  .
.
Найдём точку пересечения прямой  с осью ОУ. Ось ОУ прямая, имеющая уравнение
с осью ОУ. Ось ОУ прямая, имеющая уравнение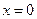 . Чтобы найти точку пересечения, решаем систему
. Чтобы найти точку пересечения, решаем систему


Ответ: (0.-2)
Упражнение 1.6
Ответы: 1) (1;1); 2) (0.5;1); 3) (2;2); 4) (3;-5)
Упражнение 1.7 Вершина А(1;-1), вершина В(2;0), вершина С(-1;3);
Упражнение 1.8.1) Искомое уравнение имеет вид  .Определяем угловой коэффициент заданной прямой
.Определяем угловой коэффициент заданной прямой  . Согласно правилу 1.2, две прямые параллельны, если
. Согласно правилу 1.2, две прямые параллельны, если 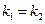 . Отсюда выписываем уравнение искомой прямой
. Отсюда выписываем уравнение искомой прямой  .
.
2)  , 3)
, 3)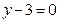 , 4) Определяем угловой коэффициент заданной прямой
, 4) Определяем угловой коэффициент заданной прямой  . Согласно правилу 1.2, прямые параллельны, если
. Согласно правилу 1.2, прямые параллельны, если 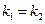 . Отсюда выписываем уравнение прямой
. Отсюда выписываем уравнение прямой 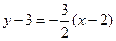 или
или  .
.
Упражнение 1.9. 1) Вначале определяем угловой коэффициент заданной прямой 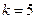 . Затем согласно правилу 1 пункт 2 б) следует,что прямые перпендикулярны, если
. Затем согласно правилу 1 пункт 2 б) следует,что прямые перпендикулярны, если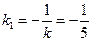 . Отсюда выписываем уравнение перпендикулярной прямой, проходящей через точку
. Отсюда выписываем уравнение перпендикулярной прямой, проходящей через точку 

2).Горизонтальная прямая перпендикулярна вертикальной прямой:
3). Вертикальная прямая перпендикулярна горизонтальной прямой:  .
.
Упражнение 1.10. ИЗ условия задачи видно, что нужно применить уравнение прямой в отрезках. Согласно формуле (1.7) и данным задачи получаем уравнение . Переходя к уравнению с угловым коэффициентом , получаем
. Переходя к уравнению с угловым коэффициентом , получаем  Отсюда
Отсюда 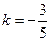 .Отсюда
.Отсюда 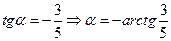 . Используя калькулятор , получаем
. Используя калькулятор , получаем  .
.
Упражнение 1.11. Используем правило1.2 и получаем ответ х=3;
Упражнение 1.13. Используем формулу (1.2) и получаем ответ 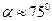
Упражнение 1.14. Используем формулу (1.10) и получаем ответ. Расстояние равно 0.3;
Упражнение 1.15. Используем формулу (1.10) и получаем ответ. Расстояние равно 2.2;
Упражнение 1.16. 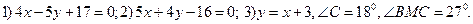
Упражнение 1.17. Искомая точка имеет координаты 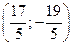 ;
;
Упражнение 1.18. 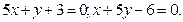
Упражнение 1.19. 
Упражнение 1.20. 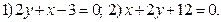
Упражнение 1.21.Указание. Обозначив искомое уравнение прямой через
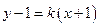 находим угловой коэффициент
находим угловой коэффициент  по формуле (1.3) (см. раздел:
по формуле (1.3) (см. раздел:
тема 1). Ответы: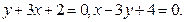
Кривые второго порядка.
Упражнение 2.2. Ответы: 1)2)Упражнение 2.3.
Эскиз такой параболы даётся в упр. 2.2 рис.4).Уравнение имеет вид 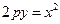 . Зная координаты фокуса, получаем по теореме 2.1
. Зная координаты фокуса, получаем по теореме 2.1 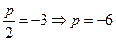 . Отсюда по формуле (2.1) получаем
. Отсюда по формуле (2.1) получаем  .
.
Упражнение 2.4.Ответ.Из теоремы 2.2 следует, что фокус лежит на оси ОХи имеет координаты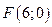 . Уравнение директрисы имеет вид:
. Уравнение директрисы имеет вид: 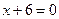 .
.
Упражнение 2.5.

Ответ: Уравнение параболы имеет вид: . Эскиз параболы представлен (на рис.1)
. Эскиз параболы представлен (на рис.1)
рис.5
Упражнение 2.7. 1) По теореме 2.3 (формула 2.6) уравнение имеет вид:
 . 2) Так как фокусы лежат на оси ОХ, то применяем формулу (2.7) получаем
. 2) Так как фокусы лежат на оси ОХ, то применяем формулу (2.7) получаем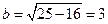 и уравнение принимает вид:
и уравнение принимает вид: 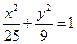 ; 3) По формуле (2.8) имеем
; 3) По формуле (2.8) имеем и
и 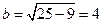 . Отсюда
. Отсюда 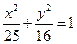 . 4) Директрисы эллипса
. 4) Директрисы эллипса
задаются уравнениями 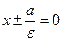 . Расстояние между этими параллельными прямыми равно
. Расстояние между этими параллельными прямыми равно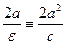 и равно 5. По условию
и равно 5. По условию 
 ; Вычисляя
; Вычисляя 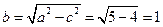 , получаем уравнение эллипса
, получаем уравнение эллипса 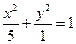 .
.
Упражнение 2.8. В этом упражнении используем теорему 2.4
Ответы : 1) , 2)
, 2)  , 3)
, 3) 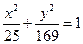 , 4)
, 4)  .
.
Упражнение 2.9. Сначала запишем каноническое уравнение эллипса: 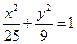 .
.
Ответы: 1) 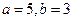 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 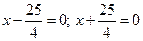 ;
;
Упражнение 2.10.
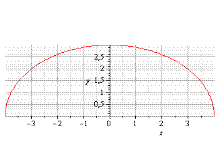
Ответы: 1) Из уравнения видно, что ордината кривой положительна. Возводим обе части уравнения в квадрат 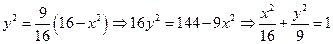 . Видно что кривая –это часть эллипса. Учитывая, что
. Видно что кривая –это часть эллипса. Учитывая, что 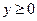 рисуем эскиз графика(рис.6).
рисуем эскиз графика(рис.6).
рис.6.
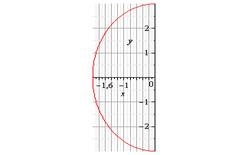 2) Абсцисса
2) Абсцисса  (рис.7) кривая часть эллипса
(рис.7) кривая часть эллипса
рис.7
Упражнение 2.11. При решении используем теорему 2.5
Ответы: 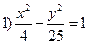 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
Упражнение 2.12.
Ответы:  2)
2)  ; 3)
; 3) 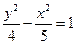 ; 4)
; 4) 
Упражнение 2.13.
Ответы: Записываем уравнение в каноническом виде . Ответы:
. Ответы:
1)  ; 2)
; 2) 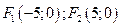 ; 3)
; 3)  ; 4)
; 4) 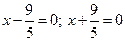 ; 5)
; 5)
Упражнение 2.14.
Ответ. Гипербола (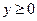 )(рис.1); Гипербола
)(рис.1); Гипербола (рис.2)
(рис.2)

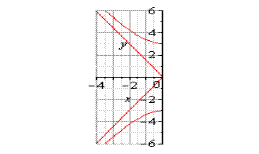
рис.8 рис.9
Упражнение 2.15.Данные кривые строим по точкам, используя калькулятор.
Кривая  .Изображена на рисунке 10.
.Изображена на рисунке 10.
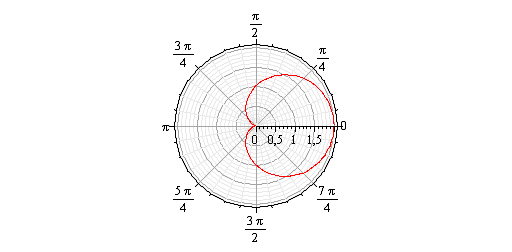
Рис.10.
Кривая 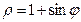 . Изображена на рисунке 11.
. Изображена на рисунке 11.
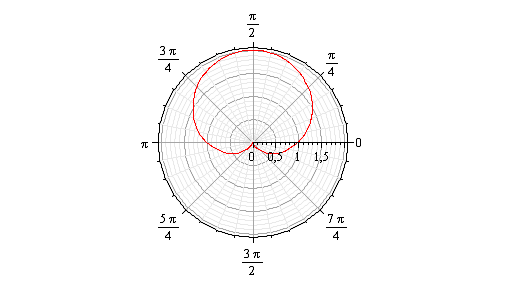
рис.11.
Кривая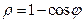 .Изображена на рисунке 12.
.Изображена на рисунке 12.

рис. 12.
Кривая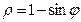 . Изображена на рисунке 4.
. Изображена на рисунке 4.
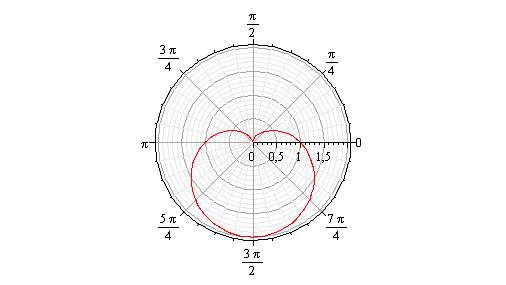
рис.13.
Упражнение 3.2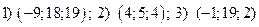
Упражнение 3.3. .
Упражнение 3.4. .
Упражнение 3.6  ; 2) вначале определяем единичный вектор в направлении вектора
; 2) вначале определяем единичный вектор в направлении вектора  . Для этого делим вектор
. Для этого делим вектор  на его длину.
на его длину.  .
.
Чтобы получить вектор длины 3 в направлении вектора  нам нужно единичный вектор умножить на 3.Искомый вектор имеет координаты
нам нужно единичный вектор умножить на 3.Искомый вектор имеет координаты 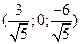 .
.
3)  .
.
Упражнение 3.7. 1) Прямая параллельна оси OX, следовательно, ответами являются единичные вектора:  .
.
2)Прямая параллельна оси OY,следовательно, ответами являются единичные вектора: .
.
3) Точки 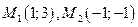 лежат на данной прямой, следовательно, вектор
лежат на данной прямой, следовательно, вектор 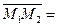
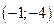 лежит на данной прямой. Коллинеарный ему единичный вектор
лежит на данной прямой. Коллинеарный ему единичный вектор
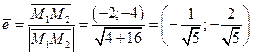 ; Ответом являются два единичных вектора:
; Ответом являются два единичных вектора: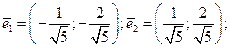
Упражнение 3.8. 1) Прямая параллельна оси OX,следовательно, ответами являются единичные вектора:
2) Прямая параллельна оси OY, следовательно, ответами являются единичные вектора:  .
.
Прямая параллельна оси OY,следовательно, ответами являются единичные вектора: .
.
3) Чтобы решить поставленную задачу нужно найти любое уравнение прямой перпендикулярной данной прямой  . По условию перпендикулярности (см. правило 1.2) одна из прямых перпендикулярных данной прямой имеет уравнение
. По условию перпендикулярности (см. правило 1.2) одна из прямых перпендикулярных данной прямой имеет уравнение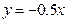 . Коллинеарный ей единичный вектор определяем аналогично
. Коллинеарный ей единичный вектор определяем аналогично
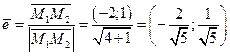 ; Ответом являются два единичных вектора:
; Ответом являются два единичных вектора: 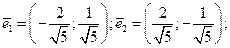
Упражнение3.9. Нет.
Упражнение 3.10. Используйте правило3.2 и формулу (3.3),(3.5),(3.6)
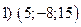 ;
; ;
;
Упражнение 3.11.Используйте формулу деления отрезка в данном отношении (3.8)
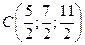 .
.
Упражнение 3.12.Используйте формулу деления отрезка в данном отношении (3.8)
 ;
;
Упражнение 3.13.Обозначим координаты искомой точки через
через  .Поформуле деления отрезка в данном отношении (3.8) получаем уравнения
.Поформуле деления отрезка в данном отношении (3.8) получаем уравнения 
 . Координаты искомой точки
. Координаты искомой точки .
.
Упражнение 3.14.Рассмотрим чертёж поставленной задачи

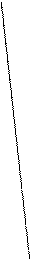

 B
B


 А C
А C
 Н
Н
D
По условию задачи 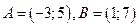 ,
, . В точке С диагонали параллелограмма делятся пополам. Чтобы найти вершину D нужно решить задачу 3.11 для отрезка BD. Чтобы найти вершину Н нужно решить задачу 3.11 для отрезка AH.
. В точке С диагонали параллелограмма делятся пополам. Чтобы найти вершину D нужно решить задачу 3.11 для отрезка BD. Чтобы найти вершину Н нужно решить задачу 3.11 для отрезка AH.
Ответ. 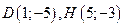 .
.
Упражнение 3.15. 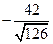 .
.
Упражнение 3.16. Используйте формулу(3.9). 
Упражнение 3.17.1)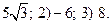 Используйте формулу(3.9).
Используйте формулу(3.9).
Упражнение 3.18.1)По правилу 3.3( пункты1,3) получаем 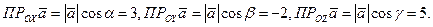
 .Отсюда вычисляем направляющие косинусы вектора
.Отсюда вычисляем направляющие косинусы вектора

Упражнение 3.19.1) Середина  ; Середина
; Середина 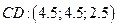 ; 2)
; 2)  ; 3) (46.2;15.4;15.4); 4)
; 3) (46.2;15.4;15.4); 4) 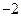 ; 5)
; 5) 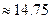 .
.
Упражнение 3.20. 
Упражнение 3.21. 
Умножение векторов.
Скалярное умножение векторов.
Упражнение 4.2.Ответ.  ;
;
Упражнение 4.3.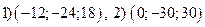 .
.
Упражнение 4.4.
Решение. 1) Сначала вычисляем векторы  =
= 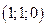 ,
,  =(
=(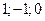 ). Затем по формуле (4.7) проекцию
). Затем по формуле (4.7) проекцию
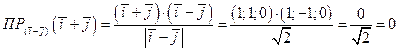
1) Сначала вычисляем векторы  затем
затем
по формуле (4.8)

Упражнение 4.5.
Решение.  . Усилие направлено противоположно направлению вектора
. Усилие направлено противоположно направлению вектора  .
. . направление усилия и направление вектора
. направление усилия и направление вектора  совпадают.
совпадают.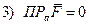 .Сила перпендикулярна направлению и поэтому никакого усилия в направлении вектора
.Сила перпендикулярна направлению и поэтому никакого усилия в направлении вектора  нет.
нет.
Упражнение 4.6. Ответ.1) 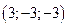 , 2) (3,-3,3).
, 2) (3,-3,3).
Упражнение 4.7.
Решение.Единичный вектор, образующий равные углы с осями координат вычисляем по формуле (4.11) : 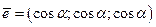 . Длина
. Длина  равна
равна
Упражнение 4.8.
Указание. Каждая координата это проекция вектора на соответствующую ось. Например, (см.формулу(4.7)) . Аналогично определяются углы
. Аналогично определяются углы 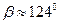 и
и  .
.
Упражнение 4.9.Указание.Для вычисления работы используйте формулу (4.9).
Ответ. А=3.
Векторное умножение векторов.
Упражнение 4.10.
Ответы. Определители вычисляем разложением по первой строке: .
.
Упражнение 4.11.
Ответы. Векторные произведения вычисляем по формуле (4.14)
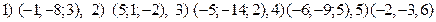
Упражнение 4.12.
Ответы. 1). Площадь вычисляем согласно формуле (4.16),с учётом,
что площадь треугольника в два раза меньше площади параллелограмма.
1 шаг. Вычисляем по формуле (4.14) векторное произведение, 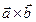 , где
, где

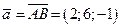 ;
;

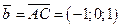
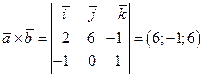
2 шаг. Находим длину векторного произведения
 . Площадь треугольника
. Площадь треугольника 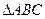 численно равна половине длины векторного произведения
численно равна половине длины векторного произведения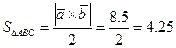 (ед.
(ед.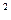 ).
).
2).Решая аналогично, получаем 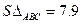 (ед.
(ед.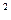 ).
).
Упражнение 4.13.Указание. Используйте формулу (4.17).
Упражнение 4.14.
Решение. Находим вектор 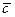 перпендикулярный заданным векторам
перпендикулярный заданным векторам 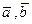
 . Вычисляем длину вектора
. Вычисляем длину вектора 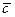 .
. 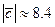 . Единичный вектор
. Единичный вектор  перпендикулярный векторам
перпендикулярный векторам 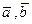 равен
равен 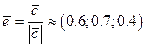 . Вектор
. Вектор  также перпендикулярен данным векторам
также перпендикулярен данным векторам 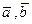 .
.
Ответ. Векторы  перпендикулярны векторам
перпендикулярны векторам 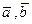 .
.
Упражнение 4.15. Все данные вектора коллинеарны вектору 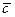 из упражнения 4.13.
из упражнения 4.13.
Ответом является вектор  , где
, где 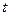 произвольный параметр.
произвольный параметр.
Смешанное произведение векторов.
Ответ. Упражнение 4.17. Решаем задачу1). Согласно формуле (4.19) вычисляем векторы… Ответ. Объём пирамиды равен (см. формулу (4.21))Плоскость в пространстве.
Упражнение 5.1.
Ответы: 1) ; 2)
; 2)  ;
;
3) найдём нормальный вектор  к искомой плоскости
к искомой плоскости 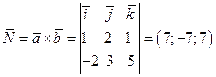 , затем запишем уравнение плоскости
, затем запишем уравнение плоскости
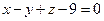 .
.
4) если точки  принадлежат плоскости, то и вектор
принадлежат плоскости, то и вектор 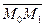
принадлежит плоскости. Аналогично и вектор 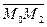 принадлежит той же плоскости .
принадлежит той же плоскости .
Полагаем 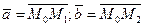 и, применяя метод решения пункта 3), получаем уравнение плоскости
и, применяя метод решения пункта 3), получаем уравнение плоскости 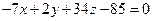 .
.
Упражнение 5.2.Расстояние вычисляем по формуле (5.9)
Ответы: 
Упражнение 5.4. Углы вычисляем по формуле (5.3)
1) 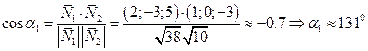
2) 
Прямая в пространстве.
Упражнение5.5.
Ответы: 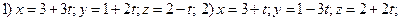
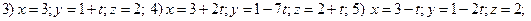
Упражнение 5.6.
Ответы: Так как точки прямой принадлежат обеим плоскостям, то решая систему уравнений находим параметрические уравнения (см.формулы(5.4)) прямой линии.
 1) Решаем систему
1) Решаем систему 
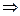 полагаем
полагаем 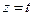
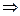
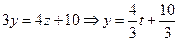
Подставляя в первое уравнение находим 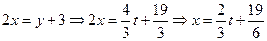 .
.
Параметрические уравнения прямой линии имеют вид 
Поступая аналогично предыдущему, получаем уравнения прямых линий
2) Параметрические уравнения имеют вид 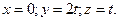
3) Параметрические уравнения имеют вид 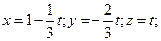
4) Параметрические уравнения имеют вид 
 Упражнение 5.7. 1) Решаем систему
Упражнение 5.7. 1) Решаем систему

Определяем параметр  ; Подставляя
; Подставляя 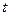 в уравнения прямой, получаем координаты точки пересечения
в уравнения прямой, получаем координаты точки пересечения 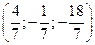 ;
;
2) прямая параллельна плоскости; 3) прямая лежит в плоскости.
Упражнение 5.8. Углы между прямыми вычисляем по формуле (5.6)
1) 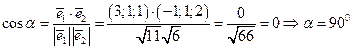
2) 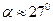 ; 3)
; 3) 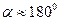 .
.
Упражнение 5.9 . Острые углы между прямыми и плоскостями вычисляем по формуле (5.8)
 ; 2)
; 2)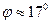 ; 3)
; 3)  ;
;
Упражнение 5.10.
Нормальным вектором к плоскости является направляющий вектор данной прямой. Определяем эти нормальные векторы к плоскостям и применяя последовательно формулы(5.1), (5.2) записываем уравнения плоскостей : 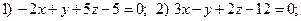
Упражнение 5.11.
1) находим пересечение данной плоскости с координатной
 плоскостью
плоскостью  . Выписываем уравнение плоскости
. Выписываем уравнение плоскости :
: 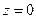 и решаем систему уравнений
и решаем систему уравнений
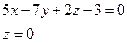 полагаем
полагаем 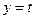 , тогда
, тогда 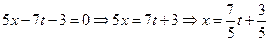
Пересечение данной плоскости с координатной плоскостью  является прямая, параметрические уравнения которой имеют вид:
является прямая, параметрические уравнения которой имеют вид: 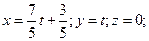
2) Пересечение данной плоскости с координатной плоскостью 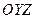
является прямая, параметрические уравнения которой имеют вид: 
3) Пересечение данной плоскости с координатной плоскостью 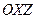 является прямая, параметрические уравнения которой имеют вид:
является прямая, параметрические уравнения которой имеют вид: 
Упражнение 5.1 2. Решение. Чтобы написать уравнение плоскости, нужно задать точку, через которую проходит плоскость и нормальный вектор  к плоскости. Осталось найти
к плоскости. Осталось найти  . Обычно в таких ситуациях используют векторное произведение.
. Обычно в таких ситуациях используют векторное произведение.
В данном случае можно положить 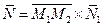 , где
, где 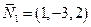 вектор нормали
вектор нормали
к плоскости  . Отсюда
. Отсюда .
.
Искомая плоскость имеет уравнение 
Для проверки правильности решения используйте правило 5.2.
Упражнение 5.13.Ответ: М
 .Указание. Используйте уравнение прямой перпендикулярной к плоскости и проходящей через точку М.
.Указание. Используйте уравнение прямой перпендикулярной к плоскости и проходящей через точку М.
Упражнение 5.14. Ответ: М
 .Указание. Используйте уравнение плоскости перпендикулярной к прямой и проходящей через точку М.
.Указание. Используйте уравнение плоскости перпендикулярной к прямой и проходящей через точку М.
 Упражнение 5.15. Ответ:
Упражнение 5.15. Ответ:  Указание. Проекция является пересечением заданной плоскости и плоскости( проходящей через точку пересечения прямой и с заданной плоскостью) и имеющую нормаль
Указание. Проекция является пересечением заданной плоскости и плоскости( проходящей через точку пересечения прямой и с заданной плоскостью) и имеющую нормаль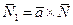 , где
, где  направляющий вектор прямой.
направляющий вектор прямой.  - нормаль к заданной плоскости.
- нормаль к заданной плоскости.