рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Абсолютна і відносна похибки
Реферат Курсовая Конспект
Абсолютна і відносна похибки
Абсолютна і відносна похибки - раздел Образование, Зміст С. Вступ..............
Зміст
С.
Вступ............................................................................................7
Розділ 1 Основні проблеми чисельного розв’язання задач...................................................................................................9
1.1 Класифікація похибок..........................................................10
1.2 Абсолютна і відносна похибки............................................13
1.3 Середні квадратичні похибки..............................................18
1.4 Поширення похибок.............................................................19
1.5 Підвищення точності результатів обчислень(рекомендації)
.............................................................................……………22
1.6 Машинна арифметика..........................................................23
1.7 Обумовленість обчислювальної задачі...............................25
1.8 Приклад втрати точності......................................................27
1.9 Погана обумовленість задачі...............................................27
1.10 Прості тести на обумовленість..........................................30
1.11 Загальна схема розв’язання задач чисельного аналізу.
Апроксимація, стійкість, збіжність...................................31
Питання і завдання до розділу 1 ...............................................33
Розділ 2 Чисельне розв’язання нелінійних рівнянь...........35
2.1 Відображення множин.........................................................35
2.2 Розв’язок рівнянь і нерухомі точки відображень .............36
2.3 Теореми про стискаючі відображення...............................38
2.4 Критерій існування нерухомих точок.................................40
2.5 Розв’язання нелінійних рівнянь у комплексній площині.41
2.6 Метод простих ітерацій........................................................44
2.7 Метод Ньютона.....................................................................51
2.8 Обумовленість задачі визначення кореня..........................57
2.9 Метод Ньютона для знаходження кратного кореня ........58
Питання та завдання до розділу 2.............................................59
Розділ 3 Розв’язування систем лінійних алгебраїчних
рівнянь (СЛАР)........................................................................61
3.1 Метод Гауcа...........................................................................62
3.2 Додаткові застосування методу Гауса................................65
3.3 Метод Краута........................................................................67
3.4 Метод прогонки....................................................................72
3.5 Ітераційні методи розв’язання СЛАР. Метод простих
ітерацій..................................................................................75
3.6 Метод Зейделя розв’язання СЛАР......................................80
3.7 Оцінка похибки і міра обумовленості................................84
Питання і завдання до теми “Розв’язання систем лінійних
алгебраїчних рівнянь точними методами”...............................92
Питання і завдання до теми “Розв’язання систем лінійних
алгебраїчних рівнянь ітераційними методами”...............……94
Розділ 4 Чисельне розв’язування систем нелінійних
рівнянь………………………………………………………...97
4.1 Метод простих ітерацій .......................................................97
4.2 Ітераційний метод Ньютона для СНАР..........................…99
4.3 Модифікований метод Ньютона ......................................101
4.4 Метод градієнтного спуску ...............................................102
4.5 Метод релаксацій................................................................108
Питання і завдання до розділу 4.............................................110
Розділ 5 Апроксимація функцій...........................................112
5.1 Поняття про наближення функцій....................................112
5.2 Iнтерполювання функції....................................................114
5.2.1 Інтерполювання за Лагранжем......................................115
5.2.2 Інтерполювання за Ньютоном.......................................117
5.2.3 Інтерполювання за Ермітом.........................................121
5.2.4 Похибка інтерполяції та способи її зменшення............122
5.2.5 Збіжність процесу інтерполяції......................................125
5.2.6 Інтерполяція за допомогою сплайнів ...........................127
5.2.7 Застосування інтерполяції для складання таблиць…..142
5.3 Метод найменших квадратів.............................................143
Питання і завдання до розділу 5.............................................155
Розділ 6 Чисельне диференціювання..................................159
6.1 Формули чисельного диференціювання...........................161
6.2 Дослідження точності чисельного диференціювання…166
6.2.1 Метод Рунге-Ромберга ...................................................167
6.2.2 Процес Ейткена………………………………………....175
Питання і завдання до розділу 6 .............................................176
Розділ 7 Чисельне інтегрування функцій………………..177
7.1 Квадратурні формули Ньютона-Котеса………………...180
7.1.1 Формула середніх (формула прямокутників)………..183
7.1.2 Формула трапецій………………………………………184
7.1.3 Формула Симпсона…………………………..…………185
7.2 Квадратурна формула Гауса……………………………..189
7.2.1 Квадратурна формула Чебишева……………………...191
7.3 Стійкість квадратурного процесу. Оцінки похибки……192
7.4 Вибір квадратурних формул чисельного інтегрування..197
7.5 Чисельне інтегрування кратних інтегралів……………..201
7.6 Вибір кубатурних формул……………………………….202
7.7 Кубатурна формула типу Симпсона ……………………207
Питання і завдання до розділу 7………………………….…210
Розділ 8 Чисельне розв’язання звичайних диференціальних рівнянь…………………………………214
8.1 Різницева апроксимація диференціальних рівнянь
однокроковими методами……………………………………217
8.1.1 Метод Ейлера…………………………………………...219
8.1.2 Схеми Рунге-Кутта другого порядку………………….224
8.1.3 Схеми Рунге-Кутта четвертого порядку……………...227
8.2 Багатокрокові методи…………………………………….235
8.2.1 Метод прогнозу і корекції……………………………..235
8.2.2 Методи Адамса………………………………………....240
8.2.3 Стійкість різницевих методів………………………….244
8.2.4 Жорсткі диференціальні рівняння…………………….248
8.3 Метод скінченних різниць………………….……………249
8.4 Різницева задача на власні значення................................254
Питання і завдання до розділу 8……………………………..255
Розділ 9 Чисельне розв’язання диференціальних рівнянь
у частинних похідних……………………………………….258
9.1 Класифікація диференціальних рівнянь у
частинних похідних…………………………………………..258
9.2 Апроксимація частинних похідних……………………...261
9.3 Метод сіток………………………………………………..263
9.4 Апроксимація для диференціальних рівнянь…………...265
9.5 Проблема збіжності методу сіток…………………….....267
9.6 Рівняння параболічного типу…………………………....269
9.6.1 Явні різницеві схеми …………………………………..271
9.6.2 Неявна різницева схема………………………………...275
9.6.3 Схема з вагами для рівняння теплопровідності………277
9.7 Різницева схема для рівняння гіперболічного типу …...283
9.8 Рівняння еліптичного типу………………………............289
Питання і завдання до розділу 9……………………………..299
Додатки.....................................................................................303
Список літератури..................................................................312
Вступ
Сучасний стан дослідження різноманітних процесів, що взаємодіють між собою, вимагає обґрунтування та побудови складних обчислювальних алгоритмів. З цією метою використовується широкий арсенал чисельних методів. Чисельними методами називають такий розділ математики, у якому предметом вивчення є методи одержання числових, з певним ступенем точності, розв’язків задач, що виникають як у самій математиці, так і в різних її додатках. Неточні (наближені) розв’язки прикладних задач заміняють їх точні розв’язки у практичних або теоретичних застосуваннях.
Створення й удосконалення швидкодіючої обчислювальної техніки дозволило розв’язати багато актуальних і складних прикладних задач, сприяло тому, що чисельні методи перетворилися в життєво необхідну сферу знань. З іншого боку, розвиток обчислювальної техніки став стимулом для критичної переоцінки та вдосконалення існуючих і створення нових чисельних методів. Найважливішим чинником при оцінці ефективності будь-якого чисельного методу в наш час є зручність його реалізації на ЕОМ. Оскільки більшість прикладних задач розв’язується на ЕОМ і надалі кількість таких задач буде збільшуватися, однією з основних проблем є подальше вдосконалення принципів і прийомів користування ЕОМ, полегшення спілкування людини з машиною.
У запропонованому Вашій увазі посібнику викладаються основні групи методів, що найчастіше застосовуються для чисельної реалізації прикладних задач. Розглядаються теоретичні основи методів, оцінки отриманих результатів та комп’ютерна реалізація чисельних алгоритмів. Для адаптації алгоритмів до різноманітних мов програмування, що використовуються зараз, пропонується використання псевдокоду. Псевдокод являє собою систему позначень і правил, призначену для одноманітного запису алгоритмів. З одного боку, він близький до звичайної природної мови, тому алгоритми можуть на ньому записуватися і читатися як звичайний текст. З іншого, - у псевдокоді використовуються деякі формальні конструкції і математична символіка, що наближає запис алгоритму до загальноприйнятого математичного запису. У псевдокоді не прийняті строгі синтаксичні правила для запису команд, властиві формальним мовам, що полегшує запис алгоритму на стадії його проектування і дає можливість використовувати більш широкий набір команд, розрахований на абстрактного виконавця. Однак використовуються деякі конструкції, властиві формальним мовам, що полегшує перехід від запису на псевдокоді до алгоритму формальною мовою.
Викладення методів та алгоритмів супроводжується прикладами чисельного розв’язання задач із використанням сучасних програмних пакетів, таких як Mathcad, Excel тощо. До кожного розділу посібника наводяться контрольні питання та завдання. Все це може зробити його корисним для використання як з метою ознайомлення з чисельними методами, так і для їх практичного застосування для розв’язання конкретних прикладних задач.
Розділ 1
Основні проблеми чисельного розв’язання задач
При застосуванні чисельних методів розв’язки задач виявляються, як правило, наближеними. Пояснюється це в багатьох випадках тим, що точні методи їх розв’язання дотепер невідомі. Крім того, навіть при застосуванні точного методу задовольняються наближеним розв’язком, зокрема, з таких причин:
— точний розв’язок виявляється трудомістким; тоді як наближений при істотно меншому об'ємі обчислень виявляється цілком прийнятним за своїм характером;
— точність отриманого результату не відіграє істотної ролі, тому що в будь-якому разі заокруглюється до цілого числа (наприклад, при визначенні кількості механізмів, необхідних для виконання даного обсягу робіт).
Наближений розв’язок задачі повинен «не набагато відрізнятися» від точного розв’язку, інакше ним не можна скористатися з конкретною метою. Що означає термін «не набагато відрізняється» або, інакше кажучи, що варто розуміти під неточністю (наближеністю) розв’язку? Кожен чисельний метод дозволяє оцінювати ступінь неточності розв’язку, одержуваного цим методом. У курсі чисельних методів ступінь неточності розв’язку характеризується поняттям похибки розв’язку. Потрібно зазначити, що теорія похибок є одним із основних розділів обчислювальної математики. Очевидно, що відхилення наближеного результату від точного напряму залежить від коректності поставленої задачі та від наявних вхідних даних. Тому актуальним є дослідження збіжності наближеного розв’язку, що пропонує чисельний алгоритм, до точного розв’язку поставленої задачі .
Таким чином, основними проблемами чисельного розв’язання задач можна вважати:
-проблему оцінки похибки наближеного розв’язку;
-проблему коректності та обумовленості поставленої задачі;
-проблему збіжності наближеного методу до точного.
1.1 Класифікація похибок
При розв’язанні прикладних задач дуже важливо мати уявлення про точність отриманих результатів. Похибки, що можуть бути закладені в таких результатах, утворюються з багатьох причин.
Можна визначити чотири основні джерела похибок результату чисельного методу:
1) вхідні дані;
2) математична модель;
3) наближений метод;
4) округлення при розрахунках.
Проаналізуємо їх.
Похибки вхідних даних
Точні значення багатьох величин практично ніколи не можуть бути введені в процес обчислень, наприклад, ірраціональних величин 
 ,
,  ,
, 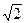 та ін. У цих випадках неминучі похибки округлення.
та ін. У цих випадках неминучі похибки округлення.
При розв’язанні багатьох задач за вхідні беруться значення величин, отриманих з експерименту. З багатьох причин, у тому числі обмеженої точності вимірювальної апаратури і впливу різних випадкових чинників, експериментальні дані завжди мають похибки того або іншого порядку. Так, точність вимірювання температури, відстані, об'єму, ваги залежить від досконалості застосовуваних вимірювальних приладів. Похибки можуть бути у вхідних даних, отриманих теоретично. Природно, що вони впливають на результати розв’язку задачі, однак жодним чином їх усунути не можна. Тому похибки такого типу часто називають неусувними.
Похибки математичної моделі
Необхідно зазначити, що в більшості випадків фахівцю вдається підібрати для розв’язання задачі наближений метод, що дозволяє одержати цілком задовільні за ступенем точності результати. Однак розв'язувана задача є не тим реальним завданням, з яким фахівцю доводиться мати справу, а його спрощеною математичною моделлю. Так, при розрахунку авіаційного двигуна або несучої конструкції промислової споруди неможливо ввести до розгляду їх реальну надзвичайно складну форму, врахувати наявність усіх отворів, деталей сполучення і т.п. При визначенні оптимального складу персоналу універмагу, кас попереднього продажу залізничних квитків доводиться припускати, що покупці приходять через рівні проміжки часу, час обслуговування кожного з них однаковий і таке інше.
Розв’язок реальної задачі не збігається із результатом, отриманим при розгляді її математичної моделі навіть із застосуванням точних методів розв’язку, а похибки, що виникають при цьому, можна назвати похибками математичного моделювання.
Похибки наближеного методу
При застосуванні наближених методів розв’язання задач, наприклад ітераційних, точні значення шуканих величин можуть бути отримані тільки після…Похибки заокруглень при розрахунках
Похибки округлення особливо доводиться враховувати при реалізації нестійких обчислювальних процесів, у яких незначні похибки у вихідних даних або… Приклад. Нехай необхідно обчислити величину за формулою , (1.1)Поширення похибок
Важливим у чисельному аналізі є питання про те, як помилка, що виникла у визначеному місці в ході обчислень, поширюється далі, тобто чи стає її… - при додаванні або відніманні чисел їхні абсолютні похибки додаються; - при множенні або діленні чисел їхні відносні похибки додаються.Машинна арифметика
. Машинний іпсилон визначається розрядністю мантиси та способом округлення… Візьмемо такі способи визначення наближених значень параметрів, необхідних у задачі:Рисунок 2.2
Виберемо деяке наближення  кореня і підставимо його в праву частину. Одержимо
кореня і підставимо його в праву частину. Одержимо 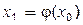 . Далі обчислюємо за формулами:
. Далі обчислюємо за формулами: 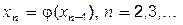 . Отримуємо послідовність наближень {
. Отримуємо послідовність наближень { } до кореня, що у випадку її збіжності до кореня
} до кореня, що у випадку її збіжності до кореня 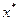 може дати наближене його значення із заданою точністю
може дати наближене його значення із заданою точністю 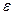 .
.
Теорема 6 Нехай функція j(x) визначена і диференційована на відрізку [a,b], причому всі значення j(х)Î [a,b] .Тоді якщо існує правильний дріб q, такий, що
½j¢(x)½£ q <1 (2.9)
при a<x<b, то: процес ітерації
xn=j(xn-1) (n = 1,2,…) (2.10)
1) збігається незалежно від початкового значення x0Î[a,b];
2) граничне значення  є єдиним коренем рівняння x=j(x) (2.11)
є єдиним коренем рівняння x=j(x) (2.11)
на відрізку [a,b].
Доведення.Розглянемо два послідовних наближення xn=j(xn-1) і xn+1=j(xn) (які внаслідок умов теореми існують). Звідси xn+1 - xn= j(xn) - j(xn-1).
Застосовуючи теорему Лагранжа, будемо мати:
xn+1 - xn = (xn - xn-1) j¢(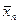 ), де
), де  .
.
Отже, на підставі умови (2.9) одержимо
 (2.12)
(2.12)
Звідси, надаючи значення n=1,2,3,…, отримаємо:
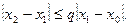 ;
;

..............................................
 (2.13)
(2.13)
Розглянемо ряд:
x0 + (x1- x0) + (x2- x1) + … + (xn – xn-1) + … , (2.14)
для якого наші послідовні наближення xn є (n+1)-ми частковими сумами, тобто xn=Sn+1. За нерівністю (2.13) члени ряду (2.14) за абсолютною величиною менші відповідних членів геометричної прогресії зі знаменником q<1, тому ряд (2.14) збігається, до того ж абсолютно. Отже, існує  , причому, вочевидь,
, причому, вочевидь,  Î[a,b]. Переходячи до границі в рівності (2.10), зважаючи на неперервність функції j(x) одержуємо
Î[a,b]. Переходячи до границі в рівності (2.10), зважаючи на неперервність функції j(x) одержуємо
 =j(
=j( ). (2.15)
). (2.15)
У такий спосіб  є корінь рівняння (2.11). Іншого кореня на відрізку [a,b] рівняння (2.11) не має. Дійсно, якщо
є корінь рівняння (2.11). Іншого кореня на відрізку [a,b] рівняння (2.11) не має. Дійсно, якщо
 , (2.16)
, (2.16)
то з рівностей (2.15) і (2.16) одержимо

і отже, 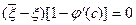 , (2.17)
, (2.17)
де c Î . Оскільки вираз у квадратній дужці в рівності (2.17) не дорівнює нулю, то
. Оскільки вираз у квадратній дужці в рівності (2.17) не дорівнює нулю, то  , тобто корінь
, тобто корінь  - єдиний.
- єдиний.
Зауваження 1 Теорема залишається правильною, якщо функція j(x) визначена і диференційована на інтервалі 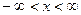 , причому при x Î (-¥;+¥) виконана нерівність (2.9).
, причому при x Î (-¥;+¥) виконана нерівність (2.9).
Зауваження 2 В умовах теореми метод ітерації збігається при будь-якому виборі початкового значення x0 Î[a,b]. Завдяки цьому він є самовиправним, тобто окрема помилка в обчисленнях, що не виводить за межі відрізка [a,b,] не вплине на кінцевий результат, тому що помилкове значення можна розглядати як нове початкове значення x0. Можливо, зросте лише обсяг роботи . Властивість самовиправлення робить метод ітерації одним із найнадійніших методів обчислень.
Оцінка наближення. З формули (2.13) маємо: 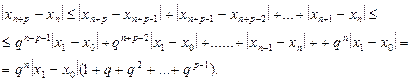
Застосувавши формулу суми геометричної прогресії, одержимо:
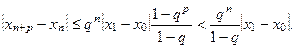
Спрямовуючи число р до нескінченності і з огляду на те, що 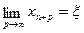 , знаходимо остаточно:
, знаходимо остаточно:
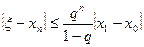 . (2.18)
. (2.18)
Звідси ясно, що збіжність процесу ітерації буде тим швидшою, чим менше число q.
Для оцінки наближення можна дати іншу формулу, корисну в деяких випадках. Представимо f(x)=x-j(x).
Очевидно, що 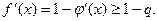 Звідси, з огляду на те, що f(x)=0, одержимо:
Звідси, з огляду на те, що f(x)=0, одержимо:
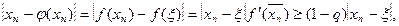
де 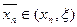 , і, отже,
, і, отже,
 (2.19)
(2.19)
тобто
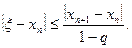 (2.20)
(2.20)
Використовуючи формулу (2.12), маємо також
 . (2.21)
. (2.21)
Звідси, зокрема, випливає, що якщо q£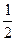 , то
, то  . В цьому випадку з нерівності
. В цьому випадку з нерівності 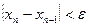 випливає нерівність
випливає нерівність
 .
.
Зауваження.Існує поширена думка, що якщо при застосуванні методу ітерації два послідовні наближення xn-1 і xn збігаються між собою із заданою точністю e (наприклад, для цих наближень установилися т перших десяткових знаків), то з тією самою точністю справедлива рівність x» xn (тобто, зокрема, у наведеному прикладі т знаків наближеного числа xn є правильними!). У загальному випадку це твердження помилкове. Більше того, легко показати, що якщо j'(х) близька до 1, то величина |x- xn| може бути великою, хоча |xn - xn-1| дуже мала.
Формула (2.20) дає можливість оцінити похибку наближеного значення xn за різницею двох послідовних наближень xn-1 і xn.
Процес ітерації варто продовжувати доти, поки для двох послідовних наближень xn-1 і xn не буде забезпечене виконання нерівності
 ,
,
де e - задана гранична абсолютна похибка кореня x і ½j¢(x)½ £ q. Тоді за формулою (2.21) будемо мати нерівність  , тобто x = xn ± e.
, тобто x = xn ± e.
Зауважимо, що якщо xn=j(xn-1) і  =j(
=j( ), то
), то  ,
, , тобто
, тобто  .
.
Таким чином, при ітераційному процесі, що збігається, похибка 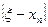 прямує до нуля монотонно, тобто кожне наступне значення xn є більш точним, ніж попереднє значення хn-1. Як правило, при всіх цих висновках ігноруються похибки округлень, тобто передбачається, що послідовні наближення знаходяться точно.
прямує до нуля монотонно, тобто кожне наступне значення xn є більш точним, ніж попереднє значення хn-1. Як правило, при всіх цих висновках ігноруються похибки округлень, тобто передбачається, що послідовні наближення знаходяться точно.
На практиці здебільшого буває так, що грубим прийомом встановлюється існування кореня рівняння (2.7) і методом ітерації потрібно одержати досить точне наближене значення кореня, причому нерівність (2.9) виконується лише в деякому околі (a, b) цього кореня. Тут при невдалому виборі початкового значення x0 послідовні наближення xn=j( xn-1) (n = 1,2,…) можуть залишити інтервал (a, b) чи навіть втратити сенс.
Приклад.Розв’язати рівняння f(x)=0 на заданому відрізку [a,b]=[0,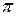 ], де
], де  =0,
=0,
Аналітичне розв’язання задачі.Розкладемо функцію  . Точні значення коренів
. Точні значення коренів 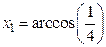 =1.31811607652818,
=1.31811607652818, 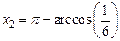 =1.738244406014586.
=1.738244406014586.
Чисельне розв’язання задачі. Локалізація кореня для чисельного розв’язання задачі
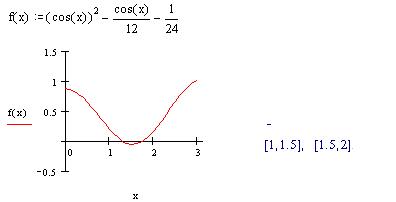 Метод бісекції, зреалізований у пакеті Mathcad, дає
Метод бісекції, зреалізований у пакеті Mathcad, дає
Перший корінь
bisec .
.
Обравши 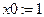 - задання початкового наближення, користуємось убудованою функцією пакета MATHCAD
- задання початкового наближення, користуємось убудованою функцією пакета MATHCAD
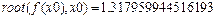 .
.
Значення кореня відрізняється від знайденого за допомогою функції bisec , тому що за замовчуванням величина похибки при роботі вбудованих функцій дорівнює 0.001.
Перевизначимо параметр для задання похибки 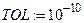
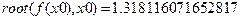 .
.
Значення кореня із заданою точністю 1.3181160717.
Другий корінь
bisec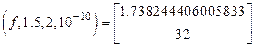 .
.
Значення кореня із заданою точністю 1.7382444060, число ітерацій 32; 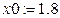 - задання початкового наближення;
- задання початкового наближення;  .
.
Значення кореня у межах заданої точності збігаються.
Метод Ньютона
, (2.22) що збігається до кореня рівняння, на відрізку локалізації кореня. Теорема 7Якщо f(a) f(b)<0, причому f¢(x) і f²(x) не дорівнюють нулю і зберігають певні знаки при a…End
f1(x):
//повертає значення першої похідної функції для данного х
End
f2(x):
//повертає значення другої похідної функції для даного х
End
//a,b – границі відрізка, eps – точність розв’язку
Solve_Nonlinear(a,b,eps):
1 if f1(a)<f1(b) then
2 min:=abs(f1(a))
Else
4 min:=abs(f1(b))
Fi
6 if f2(a)>f2(b) then
7 max:=abs(f2(a))
Else
9 max:=abs(f2(b))
Fi
11 fault:=sqrt(2*min*eps)
12 iff(b)*f2(b)>0 then
13 x:=b
Else
15 x:=a
Fi
Repeat
18 n++
19 if n>1 then
20 x:=xn
Fi
22 xn:=x-f(x)/f1(x)
23 until abs(xn-x)<=fault
24 return x
End
2.8 Обумовленість задачі визначення кореня
Нехай 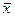 – корінь, що підлягає визначенню. Будемо вважати, що вхідними даними для задачі обчислення кореня є значення функції
– корінь, що підлягає визначенню. Будемо вважати, що вхідними даними для задачі обчислення кореня є значення функції  . Оскільки
. Оскільки  обчислюється наближено, то позначимо функцію, отриману в дійсності через
обчислюється наближено, то позначимо функцію, отриману в дійсності через 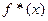 . Припустимо, що в малому околі кореня виконується нерівність:
. Припустимо, що в малому околі кореня виконується нерівність:  . Для близьких до
. Для близьких до 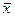 значень х справедлива рівність
значень х справедлива рівність 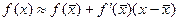 , отже,
, отже,  . Це означає, що число обумовленості задачі знаходження кореня дорівнює
. Це означає, що число обумовленості задачі знаходження кореня дорівнює 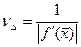 . З останньої формули можна зробити висновок, що чим менше значення похідної функції в точці кореня, тим задача гірше обумовлена. Зокрема, задача знаходження кратного кореня має число обумовленості – нескінченність.
. З останньої формули можна зробити висновок, що чим менше значення похідної функції в точці кореня, тим задача гірше обумовлена. Зокрема, задача знаходження кратного кореня має число обумовленості – нескінченність.
Інтервал невизначеності кореня. Якщо функція  неперервна, то знайдеться такий малий окіл
неперервна, то знайдеться такий малий окіл  кореня
кореня 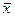 , що має радіус ε, у якому виконується нерівність
, що має радіус ε, у якому виконується нерівність  . Це означає, що для
. Це означає, що для  знак обчисленого значення
знак обчисленого значення 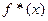 взагалі не зобов’язаний збігатися зі знаком
взагалі не зобов’язаний збігатися зі знаком  , і, отже, стає неможливим визначити, яке саме значення х з інтервалу
, і, отже, стає неможливим визначити, яке саме значення х з інтервалу  обертає функцію f в нуль. Цей інтервал називається інтервалом невизначеності кореня. Очевидно, що радіус інтервалу невизначеності для простого кореня дорівнює
обертає функцію f в нуль. Цей інтервал називається інтервалом невизначеності кореня. Очевидно, що радіус інтервалу невизначеності для простого кореня дорівнює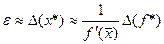 . Аналогічно можна показати, що для кратного кореня
. Аналогічно можна показати, що для кратного кореня  . Це означає, що для простого кореня радіус інтервалу невизначеності прямо пропорційний похибці обчислення функції
. Це означає, що для простого кореня радіус інтервалу невизначеності прямо пропорційний похибці обчислення функції  , а для кратного кореня
, а для кратного кореня 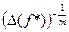 .
.
Приклад. Теоретична оцінка радіуса інтервалу невизначеності кореня.
Нехай  . Корінь рівняння простий і дорівнює
. Корінь рівняння простий і дорівнює 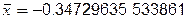 . Тоді
. Тоді  і
і  . Якщо
. Якщо 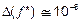 , то
, то 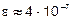 . Це означає , що знайти корінь із точністю меншою, ніж радіус інтервалу невизначеності, не вдасться.
. Це означає , що знайти корінь із точністю меншою, ніж радіус інтервалу невизначеності, не вдасться.
Метод Ньютона для знаходження кратного кореня
, де m – кратність кореня. Як правило, значення m невідоме. Використовуючи метод Ньютона, можна знайти кратність кореня. Для цього будемо задавати… Питання та завдання до розділу 2Метод Гауcа
Цей метод базується на приведенні шляхом еквівалентних перетворень вихідної системи (3.1) до вигляду з верхньою трикутною матрицею. с11x1 + c12x2 + … + c1nxn = d1 0 + c22x2 + … + c2nxn = d2Метод Краута
Тоді, за Гаусом можна явно виділити два етапи (тобто два кроки) – прямий хід… 1) ПХ:Метод прогонки
Це - ще одна модифікація методу Гауса для систем лінійних алгебраїчних рівнянь спеціального вигляду. Нехай потрібно знайти розв’язок системи так… с0у0-b0y1=f0, i=0; -aiyi-1+ciyi-biyi+1=fi, 1£ i£ N-1; (3.8)Алгоритм методу Зейделя
k- число ітерацій; x0 - вектор початкового наближення. Функція zeid повертає двовимірний масив розмірності kxn; i-й рядок якого – це…A|| = condА називають мірою обумовленості матриці. Величина відносної похибки розв’язку при фіксованій величині відносної похибки правої частини може стати як завгодно великою при досить великій мірі обумовленості матриці. Число обумовленості залежить від вибору норми матриці. Будь-яка норма матриці не менша від її найбільшого за модулем власного значення, тобто ||A||>= max||. Власні значення матриці A і A-1 взаємно обернені; тому . Таким чином, . Системи рівнянь і матриці з великими значеннями мір обумовленості прийнято називати погано обумовленими, а з малими - добре обумовленими. Отже, при розв’язуванні СЛАР на ЕОМ обов’язково виникають похибки заокруглення. Тому фактично маємо розв’язок деякої іншої системи . На практиці важливо знати відносну похибку . Якщо замість брати модель , тобто в ЕОМ задається точно, то з попередніх співвідношень випливає (- міра невизначеності розв’язку системи при неточних вхідних даних). Якщо брати систему , в якій збурені лише елементи , а b – точне, то, використовуючи співвідношення -=(), дістаємо (; cond. Лема. Якщо С-квадратна матриця така, що , то існує (І+С)-1, причому ||(І+С)-1||. Доведення. Оскільки , СЛАР має лише тривіальний розв’язок, що й означає невиродженість матриці І+С. Теорема.Нехай А – невироджена квадратна матриця. Тоді , якщо X та є відповідно розв’язками систем AХ=b та , де Ã=А+ΔА , причому , то можлива оцінка . Доведення.Оскільки , то внаслідок леми існує причому Знайдемо дістаємо шукане. Приклад реалізації чисельного алгоритму розв’язання СЛАР на псевдокоді. //Meтод Зейделя. Вважаємо, що умова збіжності методу перевірена //повертає норму матриці. А – матриця NormaMatrix(A): 1 temp:=0 2 for i:=1 to A.lengthi do 3 sum:=0 4 for j:=1 to A.lengthj do 5 sum+=abs(A[i,j])
Done
7 if sum>temp thentemp:=sum
Fi
Done
10 returntemp
End
//повертає норму вектора. В – вектор
NormaVector(B):
1 sum:=0
2 for i:=1 toB.length do
3 sum+=sqr(abs(B[i]))
Done
5 returnsqrt(sum)
End
//повертає обернену матрицю до даної A0 з точністю eps
gaussinv(A0,eps):
//доступна в модулі naz.pas
end
//розв’язує систему методом Зейделя
//A – матриця коефіцієнтів
//B – стовпець вільних членів
//X – вектор відповідей
//eps – точність обчислень
// змінні, що обчислюються, але не повертаються функцією як
// результат можуть бути використані в конкретних реалізаціях // алгоритму
Solve_Zeidel(A,B,X,eps):
1 n:=A.lengthI;
2 for i:=1 to n do //AX=B приводимо до вигляду X=CX+D
3 for j:=1 to n do
4 ifi<>j then
5 С[i,j]:=(-1)*A[i,j]/A[i,i]
6 elseС[i,j]:=0
Fi
Done
Done
10 delta:=(1-NormaVector(С))*eps/NormaVector(С)
11 for i:=1 to n do //обчислюємо A-1
12 for j=1 to n do
13 A0[i,j]:=A[i,j]
Done
Done
16 gaussinv(A0,eps)
17 condA:=norma(A)*norma(A0)
18 fault:=(condA*((0.01/norma(B))+(0.01/norma(A))))/(1-
(condA*0.04)/norma(A)); //обчислюємо похибку
19 for i:=1 to n do
20 X[i]:=B[i]
Done
22 k:=0
23 repeat//ітераційний процес
24 k++
25 maxr:=0
26 r:=0
27 for i:=1 to n do
28 xk:=X[i]
29 s:=0
30 for j:=1 to n do
31 s+=C[i,j]*X[j]
32 X[i]:=s+D[i]
Done
34 r:=abs(xk-X[i])
35 if maxr<r then
36 maxr:=r
Fi
Done
39 untilmaxr<=delta;
end
Питання і завдання до теми
“Розв’язання систем лінійних алгебраїчних рівнянь точними методами”
1 Норми векторів і матриць. Абсолютна й відносна похибки вектора.
2 Обумовленість задачі розв’язання системи лінійних алгебраїчних рівнянь. Оцінка похибки розв’язку за похибками вхідних даних: 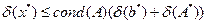 .
.
3 Метод Гауса (схема єдиного ділення):опис методу, трудомісткість методу.
4 Метод Гауса з вибором головного елемента за стовпцем (схема часткового вибору): опис методу, його обчислювальна стійкість.
5 Застосування методу Гауса для розв’язання інших задач обчислювальної алгебри.
6 Метод прогонки з тридіагональною матрицею: опис методу, умови його застосування і переваги.
7 Трудомісткість методу прогонки.
8 Матрична форма запису методу Гауса.
9 LU-розкладання матриці. Теорема про можливості застосування LU- розкладання (без доведення).
10 Застосування методу LU- розкладання для розв’язку задач обчислювальної алгебри.
11 Стратегії вибору провідного елемента в методі Гауса.
12 Метод Гаусса із частковим вибором у матричній формі.
13 Обчислити норми векторів:a)  , a=(-3, 0, 4, -5); b)
, a=(-3, 0, 4, -5); b) 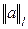 , a=(2, 6, 0); c)
, a=(2, 6, 0); c)  , a=(-13 , 7, -4,
, a=(-13 , 7, -4,
14 Обчислити норми матриць
a) , де A=
, де A=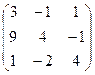 ,
,
b) , де A=
, де A= ,
,
c) , де A=
, де A=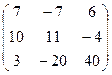 .
.
15 Чи є вираз 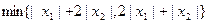 нормою вектора
нормою вектора 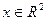 ?
?
16 Довести властивість норм матриць 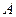 й
й  :
:  .
.
17 Нехай  . Довести, що
. Довести, що  , тоді й тільки тоді, коли
, тоді й тільки тоді, коли 
 , де
, де  - власні значення матриці
- власні значення матриці 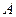 .
.
18 Перевірити справедливість властивостей числа обумовленості:
a) 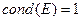 , b)
, b) 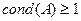 ,
,
c) 
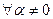 .
.
19 Оцінити кількість правильних значущих цифр розв’язку системи лінійних алгебраїчних рівнянь, якщо матриця системи 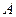 задана точно, елементи вектора правих частин задані із трьома правильними значущими цифрами, а
задана точно, елементи вектора правих частин задані із трьома правильними значущими цифрами, а  .
.
Питання і завдання до теми “Розв’язання систем лінійних алгебраїчних рівнянь ітераційними методами”
1 Розв’язати систему 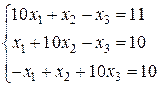 методом простої ітерації (методом Якобі) з точністю 0.01.
методом простої ітерації (методом Якобі) з точністю 0.01.
2 Зробити 3 ітерації за методом Зейделя, попередньо перетворивши системи до вигляду, зручного для ітерації. За початкове наближення взяти нульовий вектор. Зобразити графічно поведінку ітераційного процесу. Проаналізувати отримані результати з погляду збіжності (розбіжності) методу.
 ,
,  ,
, 
3 Перетворити систему до вигляду, зручного для ітерації:
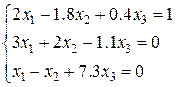
Перевірити виконання достатньої умови збіжності.
4 Переконатися в тім, що якщо A - нижня трикутна матриця, з ненульовими діагональними елементами, то метод Зейделя збігається за одну ітерацію.
5 Переконатися в тім, що якщо A - діагональна матриця з ненульовими діагональними елементами, то метод Зейделя збігається за одну ітерацію.
6 Переконатися в тім, що якщо A - верхня трикутна матриця, з ненульовими діагональними елементами, то метод Зейделя збігається за скінченне число ітерацій. Знайти цю кількість ітерацій.
7 При яких значеннях 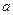 і
і  метод простої ітерації, застосований для розв’язання системи
метод простої ітерації, застосований для розв’язання системи 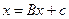 з
з  і деяким вектором
і деяким вектором  , збігається?
, збігається?
8 Нехай система  розв’язується методом Якобі
розв’язується методом Якобі 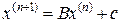 , n=0,1,…... Показати, що достатня умова збіжності методу
, n=0,1,…... Показати, що достатня умова збіжності методу 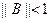 (при
(при 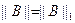 й
й 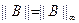 ) еквівалентна умові діагональної переваги матриці
) еквівалентна умові діагональної переваги матриці  .
.
У задачах 9-13 передбачається, що ітераційні методи розв’язання системи  записані в канонічній формі
записані в канонічній формі 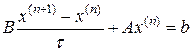 , n=0,1,…, де
, n=0,1,…, де 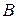 й
й 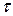 - ітераційні параметри.
- ітераційні параметри.
9 Нехай всі власні значення матриці A дійсні й додатні. Довести збіжність методу 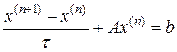 при
при  з будь-якою матричною нормою.
з будь-якою матричною нормою.
10 Нехай A - матриця простої структури й всі власні числа 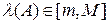 , m>0. Довести, що ітераційний метод із задачі 9 збігається при
, m>0. Довести, що ітераційний метод із задачі 9 збігається при  .
.
11 Довести, що для систем  2-го порядку метод простої ітерації (метод Якобі)
2-го порядку метод простої ітерації (метод Якобі)

і метод Зейделя:

збігаються і розбігаються одночасно. Тут 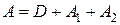 ,
, 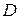 -діагональна матриця,
-діагональна матриця, 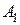 - нижня трикутна матриця,
- нижня трикутна матриця,  - верхня трикутна матриця.
- верхня трикутна матриця.
12 Довести, що для методу Зейделя необхідною й достатньою умовою збіжності є така умова: всі корені 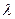 рівняння
рівняння
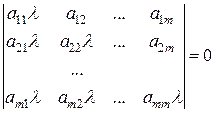
за модулем повинні бути менше 1. Тут 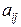 ,
,  – елементи матриці
– елементи матриці 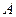 вихідної системи
вихідної системи 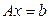 .
.
13 Довести, що якщо 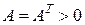 , то справедлива оцінка
, то справедлива оцінка
 ,
,  , де
, де 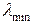 й
й  - мінімальне й максимальне власні значення матриці
- мінімальне й максимальне власні значення матриці 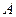 .
.
Розділ 4
Чисельне розв’язування систем нелінійних рівнянь
Розглянемо систему нелінійних рівнянь

 (4.1)
(4.1)
Представимо цю систему в матричному вигляді
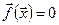 , (4.2)
, (4.2)
де 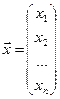 ,
,  .
.
Очевидно, для нелінійного рівняння (4.2) можна застосувати підходи, викладені в розділі 2 нашої книги, а саме там йшлося про ітераційні методи отримання наближень до кореня для нелінійних рівнянь, визначених на множинах довільної природи. Тут же йдеться про розв’язок на множині елементів з  . Розглянемо особливості застосування ітераційних методів для розв’язання систем нелінійних алгебраїчних рівнянь (СНАР).
. Розглянемо особливості застосування ітераційних методів для розв’язання систем нелінійних алгебраїчних рівнянь (СНАР).
4.1 Метод простих ітерацій
Нехай система нелінійних рівнянь (4.2) приведена до спеціального вигляду  , де функції
, де функції  дійсні, визначені і неперервні в деякій області ізольованого розв’язку
дійсні, визначені і неперервні в деякій області ізольованого розв’язку  цієї системи.
цієї системи.
Як відомо з розділу 2, для визначення вектора-кореня  цієї системи зручно користуватися методом простої ітерації, де ітераційний процес організується за формулою
цієї системи зручно користуватися методом простої ітерації, де ітераційний процес організується за формулою  , обравши якесь початкове наближення
, обравши якесь початкове наближення 
 .
.
Уведемо 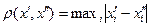 . Нехай кожне рівняння системи має вигляд
. Нехай кожне рівняння системи має вигляд  , причому задовольняє умову Ліпшиця
, причому задовольняє умову Ліпшиця  , тоді при
, тоді при 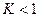 цей ітераційний процес збігається. Цей факт випливає з принципу стискаючих відображень, причому
цей ітераційний процес збігається. Цей факт випливає з принципу стискаючих відображень, причому 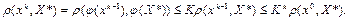
Якщо R – сукупність векторів 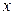 , для яких
, для яких  , то в R є єдиний розв’язок. Розглянемо матриці
, то в R є єдиний розв’язок. Розглянемо матриці 
Далі – як в ітераційних процесах. Для того щоб ітераційний процес збігався, необхідно й достатньо виконання умови  , при
, при  . Цю умову важко перевірити, тому використовується достатня умова
. Цю умову важко перевірити, тому використовується достатня умова 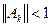 при будь-якому k .
при будь-якому k .
При виконанні умов збіжності ітераційного процесу для розв’язання системи нелінійних рівнянь можна застосовувати аналог методу Зейделя:

Теорема 1 Нехай область G замкнена і відображення 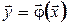 є стискаючим у G, тобто виконана умова
є стискаючим у G, тобто виконана умова  . Тоді, якщо для ітераційного процесу
. Тоді, якщо для ітераційного процесу  всі послідовні наближення x(p)є G, то:
всі послідовні наближення x(p)є G, то:
1) незалежно від вибору початкового наближення ітераційний процес збігається, тобто існує
 при
при 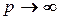 ;
;
2) граничний вектор x* є єдиним розв’язком рівняння  в G ;
в G ;
3) справедлива оцінка  .
.
Теорема 2 Нехай 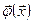 і
і 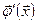 неперервні в області G, причому в G виконується нерівність
неперервні в області G, причому в G виконується нерівність
 .
.
Якщо послідовні наближення 
не виходять з G, то процес ітерації збігається і граничний вектор  при
при 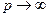 є в G єдиним розв’язком.
є в G єдиним розв’язком.
4.2 Ітераційний метод Ньютона для СНАР
Нехай, керуючись підходами, викладеними в розділі 2, знайдено p-е наближення
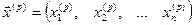
одного з ізольованих коренів 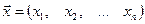 векторного рівняння (4.2). Тоді точний корінь можна подати у вигляді
векторного рівняння (4.2). Тоді точний корінь можна подати у вигляді
 , (4.3)
, (4.3)
де 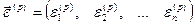 - похибка кореня.
- похибка кореня.
Підставимо (4.3) у (4.2):
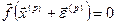 . (4.4)
. (4.4)
Нехай  – неперервна диференційована функція в деякій опуклій області, що містить
– неперервна диференційована функція в деякій опуклій області, що містить  і
і  , розкладемо ліву частину (4.4) в ряд за степеням малого вектора
, розкладемо ліву частину (4.4) в ряд за степеням малого вектора 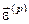 , обмежившись лінійними членами:
, обмежившись лінійними членами:
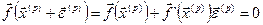 (4.5)
(4.5)
З (4.5) випливає, що під 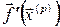 треба розуміти матрицю Якобі системи функцій f1, f2,…,fn щодо x1,x2,…,xn
треба розуміти матрицю Якобі системи функцій f1, f2,…,fn щодо x1,x2,…,xn

Система (4.5) являє собою систему лінійних рівнянь відносно похибок 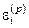 (i=1,2,…,n) з матрицею W(x), тому формула (4.5) набере вигляду
(i=1,2,…,n) з матрицею W(x), тому формула (4.5) набере вигляду
 .
.
Допускаючи, що W(x)– невироджена, знаходимо
 ,
,
значить,
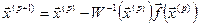 . (4.6)
. (4.6)
Отримали інтерполяційну формулу Ньютона для СНАР. Очевидно, формула (4.6) дозволить побудувати збіжну до кореня ітераційну послідовність за умови, що відображення 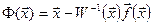 буде стискаючим. Для цього треба правильно обрати нульове наближення
буде стискаючим. Для цього треба правильно обрати нульове наближення  .
.
Теорема 3. Маємо нелінійну систему рівнянь з дійсними коефіцієнтами (4.2), де вектор-функція визначена і неперервна разом зі своїми частковими похідними 1-го і 2-го порядків в області w. Вважатимемо, що  є точка, яка лежить у w разом зі своїм замкненим
є точка, яка лежить у w разом зі своїм замкненим  -околом. Причому виконані умови:
-околом. Причому виконані умови:
1) Матриця Якобі при 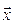 =
= має обернену Г0, де ||Г0||<=A0, (в змісті m-норми)
має обернену Г0, де ||Г0||<=A0, (в змісті m-норми)
2) ||Г0f(x0)||<=B0<=H/2
3) 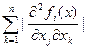 <=C при i,j=1,2,…,n
<=C при i,j=1,2,…,n
4) постійні A0, B0 і C задовольняють нерівність m0=2n0B0C<=1
Тоді процес Ньютона (4.6) при початковому наближенні  збігається і граничний вектор
збігається і граничний вектор 
є розв’язком системи таким, що ||x*-x0||<=2B0<=H.
4.3 Модифікований метод Ньютона
При побудові процесу Ньютона (4.6) істотною незручністю є необхідність для кожного кроку заново обчислювати обернену матрицю Якобі. Якщо ця матриця неперервна в околі шуканого розв’язку x0, досить близького до x*, то приблизно можна покласти

і ми приходимо до модифікованого методу Ньютона
 .
.
4.4 Метод градієнтного спуску
Припустимо, що в системі нелінійних алгебраїчних рівнянь (4.2) функції fi дійсні і неперервно диференційовані в їхній загальній області визначення. Розглянемо функцію
 . (4.7)
. (4.7)
Очевидно, що кожен розв’язок системи (4.2) перетворює в нуль функцію U(x); і навпаки, числа x1,x2,...,xn, для яких функція U(x) дорівнює нулю, є коренем системи (4.2).
Припустимо, що система має лише ізольований розв’язок, що являє собою точку строгого мінімуму функції U(x) у n-вимірному просторі  ={x1,x2,..., xn }.
={x1,x2,..., xn }.
Нехай  - корінь системи (4.2) і
- корінь системи (4.2) і  - його нульове наближення. Через точку
- його нульове наближення. Через точку  проведемо поверхню рівня функції U(
проведемо поверхню рівня функції U( ). Якщо точка
). Якщо точка  досить близька до кореня
досить близька до кореня  , то при наших припущеннях поверхня рівня U(
, то при наших припущеннях поверхня рівня U( )=U(
)=U( ) буде схожа на еліпсоїд.
) буде схожа на еліпсоїд.
З точки  рухаємося по нормалі до поверхні U(
рухаємося по нормалі до поверхні U(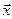 )=U(
)=U( ) доти, поки ця нормаль не доторкнеться в деякій точці
) доти, поки ця нормаль не доторкнеться в деякій точці  іншої поверхні рівня U(
іншої поверхні рівня U( )= U(
)= U( ).
).
Потім, відправляючись від точки  , знову рухаємося по нормалі до поверхні рівня U(
, знову рухаємося по нормалі до поверхні рівня U( )= U(
)= U( ) доти, поки ця нормаль не доторкнеться в деякій точці
) доти, поки ця нормаль не доторкнеться в деякій точці 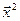 нової поверхні рівня U(
нової поверхні рівня U( )= U(
)= U(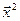 ), і т.д.
), і т.д.
Оскільки U( )>U(
)>U( )>U(
)>U(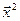 )>..., то, рухаючись таким чином, ми швидко наближаємося до точки з найменшим значенням U ("дно ями"), що відповідає кореневі системи (4.2). Позначимо через
)>..., то, рухаючись таким чином, ми швидко наближаємося до точки з найменшим значенням U ("дно ями"), що відповідає кореневі системи (4.2). Позначимо через

градієнт функції U( ). Визначимо описаний алгоритм пошуку точок-наближень за формулою
). Визначимо описаний алгоритм пошуку точок-наближень за формулою
 . (4.8)
. (4.8)
Залишається визначити множники lp. Для цього розглянемо скалярну функцію 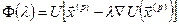 .
.
Функція F(l) дає зміну рівня функції U уздовж відповідної нормалі до поверхні рівня в точці  . Множник l=lp потрібно вибрати таким , щоб F(l) мала мінімум. Керуючись необхідною умовою екстремуму функції, одержуємо рівняння
. Множник l=lp потрібно вибрати таким , щоб F(l) мала мінімум. Керуючись необхідною умовою екстремуму функції, одержуємо рівняння
 .
. (4.9)
(4.9)
Найменший додатний корінь цього рівняння і дасть нам значення lp. Будемо вважати, що l - мала величина, квадратом і вищими ступенями якої можна зневажити. Маємо  . Розкладаючи функції fi за степенями l з точністю до лінійних членів, одержимо
. Розкладаючи функції fi за степенями l з точністю до лінійних членів, одержимо
 ,
,
де 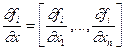 . Звідси
. Звідси
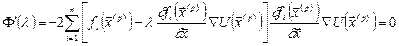
Отже, 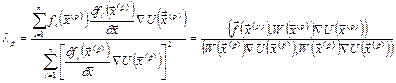 ,
,
де  - матриця Якобі. Далі маємо
- матриця Якобі. Далі маємо
 .
.
Звідси  ,
,
де W`(x) - транспонована матриця Якобі. Тому остаточно 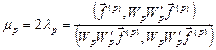 , а
, а  . Отримали розрахункову формулу методу градієнтного спуску з визначенням кроку.
. Отримали розрахункову формулу методу градієнтного спуску з визначенням кроку.
Сучасна комп’ютерна техніка дозволяє суттєво спростити цей метод розв’язання нелінійних систем. Множник lp у формулі (4.8) обирають як достатньо малий постійний крок у напрямку антиградієнта. Наприклад, lp=0.00001.
Приклад. Розв’язати систему нелінійних рівнянь з точністю e=0,0001
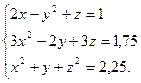
Скористаємося методом градієнтного спуску. Для цього побудуємо функцію  , де
, де  , а
, а 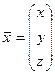 .
.
Кожен розв’язок системи - це нуль функції  і навпаки. Виберемо початкове наближення
і навпаки. Виберемо початкове наближення 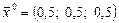 . Позначимо
. Позначимо  Пошук розв’язку проводимо за формулою
Пошук розв’язку проводимо за формулою
 .
.
Множник l(p) визначається так:  , де:
, де:
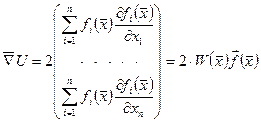 .
.
Тоді процес здійснюється за формулою
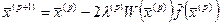 ;
;
W – матрица Якобі: 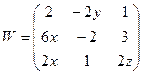 .
.
Пошук наближень до розв’язку припиняється за умови  .
.
Реалізація алгоритму на псевдокоді:
VectorF(F,x):
//розраховуємо коефіцієнти вектора F при x
end
VectorW(W,x):
//розраховуємо коефіціенти матриці W при x
end
//W – матриця Якобі
//F – матриця системи
//Z – результат множення
multWF(W,F,Z): // множення W на F
15 for i:=1 to W.lengthI do
16 for j:=1 to W.lengthJ do
17 Z[i]+=W[i,j]*F[j]
Done
Done
End
//A – вихідна матриця
//X – транспонована матриця
Transpon(A,X):
1 for i:=1 to A.lengthI do
2 for j:=1 to A.lengthJ do
3 if i=j then
4 X[i,j]:=A[i,j]
Else
6 X[i,j]:=A[j,i]
Fi
Done
Done
End
Scalar(A,B): //скалярний добуток векторів a та b
1 s:=0
2 for i:=1 to A.length do
3 s+=A[i]*B[i]
Done
5 return s
end
// розв’язання нелінійної системи методом градієнтного спуску
Solve_NonLinear_System(F,W,X):
1n:=A.lengthI
2 for i:=1 to n do
3 X[i]:=-1;
Done
5k:=0
Repeat
7k++
8 for i:=1 to n do
9 XK[i]:=X[i]
Done
11Vectorf(F,xk)
12MatrixW(W,xk)
13MultWF(wt,f,u)
14MultWF(w,u,z)
15mu:=(scalar(f,z))/(scalar(z,z))
16maxr:=0
17 for i:=1 to n do
18 X[i]:=XK[i]-mu*U[i]
19 if abs(X[i]-XK[i])>maxr then
20 maxr:=abs(X[i]-XK[i])
Fi
22 untilmaxr<eps
Done
end.
Відповідь: X=0.50, Y=1.00, Z=1.00.
4.5 Метод релаксацій
Перепишемо систему (4.1) у вигляді
 =
=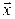 +
+
 ,
,
де  - деяка константа, і побудуємо ітераційний процес за схемою
- деяка константа, і побудуємо ітераційний процес за схемою
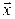 (k+1) =
(k+1) = 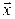 (k) +
(k) +
 .
.
Параметр  повинен бути таким, щоб в околі pозв’язку виконувалася достатня умова збіжності
повинен бути таким, щоб в околі pозв’язку виконувалася достатня умова збіжності
||Е+ W|| < 1,
W|| < 1,
де E- одинична матриця, а W –матриця Якобі. На практиці виконання цієї умови досить складно перевірити, тому значення параметра  вибирають пробним шляхом, перевіряючи виконання необхідної умови збіжності після здійснення кожної ітерації
вибирають пробним шляхом, перевіряючи виконання необхідної умови збіжності після здійснення кожної ітерації
|| (k)-
(k)- (k-1)||<||
(k-1)||<|| (k-1)-
(k-1)-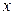 (k-2)||.
(k-2)||.
Якщо виявиться, що на якій-небудь ітерації ця умова не виконується, то необхідно змінити значення параметра  .
.
 Приклад.Знайти з точністю
Приклад.Знайти з точністю 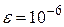 всі корені системи нелінійних рівнянь
всі корені системи нелінійних рівнянь 
використовуючи метод Ньютона для системи нелінійних рівнянь. Знайти корінь за допомогою убудованого блоку розв’язку рівнянь Given Find пакета MATHCAD. Рівняння системи:

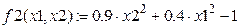 .
.
Локалізація кореня
Перше рівняння, визначене відносно x2:  . Друге рівняння, визначене відносно x2:
. Друге рівняння, визначене відносно x2:  .
.
Маємо 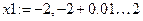 .
.

Перший корінь
Початкове наближення: 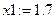
 .
.
Точність для блоку Given Find: TOL:= 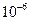 .
.
Розв’язання системи f(x1,x2)=0 за допомогою убудованого блоку MATHCAD:
Given

 0
0
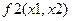
 0
0
 Find(
Find(
Отриманий наближений розв’язок  .
.
Питання і завдання до розділу 4
1 Постановка задачі розв’язання системи нелінійних рівнянь. Основні етапи розв’язування задачі.
2 Метод простої ітерації: опис методу, умова й швидкість збіжності, критерій закінчення, приведення до вигляду, зручного для ітерацій.
3 Метод Ньютона: опис методу, теорема про збіжність, критерій закінчення.
4 Недоліки методу Ньютона. Модифікації методу Ньютона.
5 Застосування методів розв’язання систем нелінійних рівнянь для задачі мінімізації функцій.
6 Розв’язати методом Ньютона з точністю 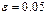 системи рівнянь:
системи рівнянь:
a)  ,
,  ;
;
b)  ,
,  .
.
7 Чи можна стверджувати, що система має, й до того ж єдиний, розв’язок?
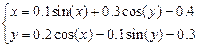
8 Для системи рівнянь виписати розрахункові формули методу релаксацій:
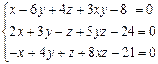
9 Розв’язати методом простої ітерації такі системи:
a)
 ,
,  ;
;
b) 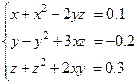 ,
, 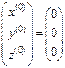 .
.
10 Для функції  знайти точки мінімуму, звівши задачу до розв’язання системи рівнянь.
знайти точки мінімуму, звівши задачу до розв’язання системи рівнянь.
Розділ 5
Апроксимація функцій
Апроксимація (від лат. approximo - наближаюся) - заміна одних математичних об'єктів іншими, якомось чином близькими до вихідних. Апроксимація дозволяє досліджувати числові характеристики і якісні властивості об'єкта, зводячи задачу до вивчення більш простих або більш зручних об'єктів (наприклад таких, характеристики яких легко обчислюються або властивості яких уже відомі). У теорії чисел вивчаються діофантові наближення, зокрема наближення ірраціональних чисел раціональними. У геометрії і топології розглядаються апроксимації кривих, поверхонь, просторів і відображень. Деякі розділи математики цілком присвячені апроксимації, наприклад наближення функцій.
5.1 Поняття про наближення функцій
Нехай величина у є функцією аргумента х. Це означає, що будь-якому значенню х з області визначення поставлено у відповідність значення у. Разом з тим на практиці часто невідомий явний зв'язок між у та х, тобто неможливо записати цей зв'язок у вигляді деякої залежності y=f(x). У деяких випадках навіть при відомій залежності y=f(x) вона настільки громіздка (наприклад, містить вирази, що важко обчислюються, складні інтеграли і т.п.), що її використовувати в практичних розрахунках важко.
Найбільш поширеним і практично важливим випадком, коли вигляд зв'язку між параметрами х та у невідомий, є його завдання у вигляді деякої таблиці {xi, yi}. Це означає, що дискретній множині значень аргумента {xi} поставлена у відповідність множина значень функції {yi} (i=0,1,…,n). Ці значення - або результати розрахунків, або експериментальні дані. На практиці нам можуть знадобитися значення величини у і в інших точках поза вузлами xi. Однак одержати ці значення можна лише шляхом дуже складних розрахунків або проведенням дорогих експериментів.
Таким чином, з огляду економії часу і засобів ми приходимо до необхідності використання наявних табличних даних для наближеного обчислення невідомого параметра у при будь-якому значенні (з деякої області) визначального параметра х, оскільки точний зв'язок y = f(x) - невідомий.
Цій меті підпорядкована задача про наближення (апроксимацію) функцій: задану функцію f(x) потрібно приблизно замінити (апроксимувати) деякою функцією F(x) так, щоб відхилення (у деякому змісті) F(x) від f(x) у заданій області було найменшим. Функція F(x) при цьому називається апроксимуючою.
Апроксимуючими функціями можуть бути поліноміальні, тригонометричні, експонентні та ін.
Якщо наближення будується на заданій дискретній множині точок {xi}, то апроксимація називається точковою. До неї належать інтерполяція, середньоквадратичне наближення та ін. При побудові наближення на неперервній множині точок (наприклад, на відрізку [a,b]) апроксимація називається неперервною (або інтегральною).
Одним із основних типів точкової апроксимації є інтерполяція. У цьому випадку апроксимуюча функція проходить через задані вузлові точки. Іноді наближення табличних даних методом інтерполяції проводити незручно. Так, наприклад, якщо дані в таблиці неточні, то збіг значень інтерполяційної функції у вузлах з табличними даними означає, що вона точно повторює помилки таблиці. У таких випадках використовують інші види апроксимації, наприклад, метод найменших квадратів. Цим методом апроксимуюча функція будується так, щоб сума квадратів відстаней від ординат точок до лінії графіка апроксимуючої функції для однакових абсцис була найменшою.
5.2 Iнтерполювання функції
Загальна постановка задачі інтерполювання така. Задані значення  функції аргумента
функції аргумента 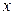 при відповідних його значеннях
при відповідних його значеннях 
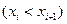 . Побудувати неперервну функцію
. Побудувати неперервну функцію  , що належить до заданого класу функцій, таку, що вона збігається з
, що належить до заданого класу функцій, таку, що вона збігається з  при значеннях аргумента
при значеннях аргумента 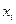
 . Така функція називається інтерполюючою. Точки xi, i=1,…,n називаються вузлами інтерполяції і вони утворюють сітку розбиття
. Така функція називається інтерполюючою. Точки xi, i=1,…,n називаються вузлами інтерполяції і вони утворюють сітку розбиття  , а yi - вузловими значеннями.
, а yi - вузловими значеннями.
У такому формулюванні розв'язок задачі є невизначеним, бо крізь задані точки можна провести безліч кривих. Тому загальну постановку дещо звужують, задаючи не тільки клас інтерполюючої функції, але й додаткову умову мінімальної її складності.
Наприклад, для найбільш поширеного поліноміального інтерполювання (при якому інтерполююча функція обирається серед поліномів аргумента 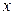 ), додатковою умовою є мінімальний порядок інтерполюючого полінома. З цього випливає, що якщо первісну функцію задано лише двома точками, її треба інтерполювати поліномом першого порядку (через дві задані точки проходить єдина пряма), якщо трьома - параболою другого порядку і так далі. Взагалі функція, задана своїми
), додатковою умовою є мінімальний порядок інтерполюючого полінома. З цього випливає, що якщо первісну функцію задано лише двома точками, її треба інтерполювати поліномом першого порядку (через дві задані точки проходить єдина пряма), якщо трьома - параболою другого порядку і так далі. Взагалі функція, задана своїми  значеннями (у
значеннями (у  точках), інтерполюється однозначно поліномом
точках), інтерполюється однозначно поліномом  -го порядку, тобто таким
-го порядку, тобто таким
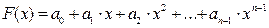 . (5.1)
. (5.1)
Тепер задача інтерполювання звелася до пошуку значень 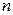 невідомих коефіцієнтів полінома (5.1) з умови набуття ним значень
невідомих коефіцієнтів полінома (5.1) з умови набуття ним значень  при значеннях аргумента
при значеннях аргумента 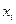
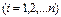 .
.
Існують кілька способів визначення цих коефіцієнтів. Вони відрізняються методикою обчислень, зручною в одних і незручною в інших випадках. Але при ідеальних обчисленнях вони, природно, призводять до тих самих результатів, тобто до того самого полінома.
Нтерполювання за Лагранжем
За цією методикою попередньо визначають допоміжні поліноми -го порядку такі, що . (5.2) Тобто кожен із них набуває значення 1 тільки при , а для решти заданих значень аргумента він дорівнює нулю. Такі…Нтерполювання за Ньютоном
Недоліком інтерполювання за Лагранжем є те, що якщо для поліпшення наближення додати ще один вузол інтерполювання, доведеться всі обчислення… На практиці часто трапляються випадки, коли вузли інтерполяції стають відомими… Нехай вузли інтерполяції рівновіддалені один від одного за аргументом, тобто виконується умоваEnd
//X – значення аргумента
//Y – значення функції
//xi – значення аргумента, для якого потрібно знайти значення
// функції
//h – крок
//змінні DY, D2Y і т.д. – скінченні різниці
//змінні SDY, SD2Y і т.д. – розділені різниці
//відшукуємо значення інтерполюючого многочлена при x=xi
Find_PX(X,Y,n,h):
1 n:=X.length;
2 for i:=1 to n do
3 DY[i]:=Y[i+1]-Y[i]
Done
5 for i:=1 to (n-1) do
6 D2Y[i]:=DY[i+1]-DY[i]
Done
8 for i:=1 to (n-2) do
9 D3Y[i]:=D2Y[i+1]-D2Y[i]
Done
11 for i:=1 to (n-3) do
12 D4Y[i]:=D3Y[i+1]-D3Y[i]
Done
14 for i:=1 to n do
15 SDY[i]:=Y[i+1]-Y[i]/(X[i+1]-X[i])
Done
17 for i:=1 to (n-1) do
18 D2Y[i]:=SDY[i+1]-SDY[i]/(X[i+2]-X[i])
Done
20 for i:=1 to (n-2) do
21 D3Y[i]:=SD2Y[i+1]-SD2Y[i]/(X[i+3]-X[i])
Done
23 for i:=1 to (n-3) do
24 D4Y[i]:=SD3Y[i+1]-SD3Y[i]/(X[i+4]-X[i])
Done
26 t:=(xi-X[1])/h
27 return X[1]+(t/factorial(1))*DY[1]+((t*(t-1))/factorial(2))*D2Y[1]+((t*(t-1)*(t-2))/factotrial(3))*D3Y[1]+((t*(t-1)*(t-2)*(t-3))/factorial(4))*D4Y[1];
End
//R – дані сплайна
//eps – точність обчислень
//xi – значення аргумента, при якому потрібно знайти значення функції //
//відшукуємо значення кубічного сплайна в точці xi
Find_Spline(R,eps,xi)
1 linequ(R,R.length,1E-6,М)
2 k:=2
3 s31:=(X[k+1]-xi)*(X[k+1]-xi)*(2*(xi-X[k])+1)*Y[k]+(xi-X[k])*(xi-X[k])*(2*(X[k+1]-xi)+1)*Y[k+1]
4 s32:=(X[k+1]-xi)*(X[k+1]-xi)*(xi-X[k])*M[k]+(xi-X[k])*(xi-X[k])*(xi-X[k+1])*М[k+1]
5 return s31+s32
end
Оцінка похибки та збіжності при інтерполяції кубічними сплайнами
Якщо 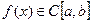 , то похибка інтерполяції кубічним сплайном
, то похибка інтерполяції кубічним сплайном
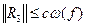 , де
, де 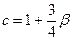 ,
,  .
.
Якщо 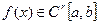 , r=1,2,3,4, то оцінка має вигляд для
, r=1,2,3,4, то оцінка має вигляд для 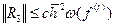 .
.
Із цих оцінок треба встановити збіжність інтерполяційного процесу на послідовності сіток 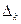 .
.
Для простоти обчислень або при труднощах у пошуку першої та другої похідних заданої функції можна застосувати таку оцінку похибок:
 .
.
Приклад. Апроксимувати функції  на відрізку [-2;2] , використовуючи лінійний сплайн і природний кубічний сплайн.
на відрізку [-2;2] , використовуючи лінійний сплайн і природний кубічний сплайн.
Дослідження проведемо на рівномірних сітках з кількістю вузлів інтерполяції : 5, 7, 9, 15 , 51 , 101 відповідно. Визначимо відносну похибку інтерполяції сплайнами на різних сітках. Результати занесемо до таблиці.
Аналіз результатів показує, що точність апроксимації істотно залежить від кількості вузлових точок.
| Число вузлів | Лінійний сплайн | Кубічний сплайн | Куб. сплайн по другій похідній |
| 0,0625 | 0,024 | 0,0092 | |
| 0,0278 | 0,011 | 0,0038 | |
| 0,0156 | 0,0061 | 0,002 | |
| 0,0051 | 0,002 | 0,0007 | |
| 0,0004 | 0,00016 | 0,000055 | |
| 0,0001 | 0,000036 | 0,000014 |
Апроксимаційні властивості кубічного сплайна
Апроксимаційні властивості кубічного сплайна залежать від гладкості функції 
 - чим вище гладкість інтерпольованої функції, тим вище порядок апроксимації при подрібленні сітки і тим швидшою є збіжність.
- чим вище гладкість інтерпольованої функції, тим вище порядок апроксимації при подрібленні сітки і тим швидшою є збіжність.
Якщо інтерпольована функція  неперервна на відрізку
неперервна на відрізку  , тобто
, тобто 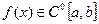 , то
, то
 при
при 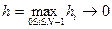 .
.
Якщо інтерпольована функція  має на відрізку
має на відрізку  неперервну першу похідну, тобто
неперервну першу похідну, тобто 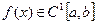 , а
, а  - інтерполяційний сплайн, що задовольняє граничні умови 1-го або 3-го типу, то при
- інтерполяційний сплайн, що задовольняє граничні умови 1-го або 3-го типу, то при 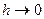
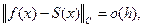

У цьому випадку не тільки сплайн збігається до інтерпольованої функції, але і похідна сплайна збігається до похідної цієї функції.
На випадок, якщо 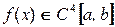 , сплайн
, сплайн  апроксимує на відрізку
апроксимує на відрізку  функцію
функцію  , а його 1-а та 2-а похідні апроксимують відповідно функції
, а його 1-а та 2-а похідні апроксимують відповідно функції  та
та  :
: 
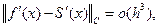
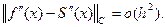
5.2.7 Застосування інтерполяції для складання таблиць
Теорія інтерполяції має застосування при складанні таблиць функцій. Одержавши завдання на складання таблиць тих чи інших функцій, математик повинен вирішити перед початком обчислень ряд питань. Повинна бути обрана формула, за якою будуть проводитися обчислення. Ця формула може змінюватися від ділянки до ділянки. Як правило, формули для обчислення значень функції бувають громіздкими і тому їх використовують для одержання деяких опорних значень і потім, шляхом субтабулювання, згущують таблицю. Формула, що дає опорні значення функції, повинна забезпечувати потрібну точність таблиць із врахуванням наступного субтабулювання . Якщо передбачається скласти таблиці з постійним кроком, то спочатку необхідно визначити крок таблиці.
Найчастіше таблиці функцій складаються так, щоб була можлива лінійна інтерполяція ( тобто інтерполяція з використанням перших двох членів формули Тейлора). У цьому випадку залишковий член буде мати вигляд  . Тут x належить інтервалу між двома сусідніми табличними значеннями аргумента, у якому лежить х, а
. Тут x належить інтервалу між двома сусідніми табличними значеннями аргумента, у якому лежить х, а  . Добуток t(t – 1) набуває найбільшого за модулем значення при
. Добуток t(t – 1) набуває найбільшого за модулем значення при 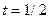 . Це значення дорівнює
. Це значення дорівнює  Отже,
Отже,  де
де 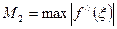 .
.
Щоб помилка інтерполяції не перевищувала за абсолютною величиною деяке а, необхідно вибрати h, яке задовольняло б умову 
5.3 Метод найменших квадратів
Аналізуючи попереднє, можна зазначити, що інтерполювання може бути здійснене лише на невеликому інтервалі по кількох вузлах інтерполяції, процес обчислення скінченних різниць є нестійким. Окрім того, якщо значення  подають значення функції, яка наближується, зі значними похибками, інтерполювати ці значення недоцільно.
подають значення функції, яка наближується, зі значними похибками, інтерполювати ці значення недоцільно.
За таких умов застосовують середньоквадратичне наближення. Найбільш ефективним методом побудови середньоквадратичного наближення функції є метод найменших квадратів (МНК).
Нехай є відомими 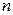 значень
значень 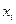 (
(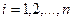 ) деякої фізичної величини
) деякої фізичної величини  , виміряної у моменти часу
, виміряної у моменти часу  . Припустимо, що ці значення подають істинні значення функції
. Припустимо, що ці значення подають істинні значення функції  у відповідні моменти часу зі значними похибками, значення яких невідомі, але припускається, що ці похибки є випадковими з математичним сподіванням, що дорівнює нулю. Будемо наближати невідому функцію
у відповідні моменти часу зі значними похибками, значення яких невідомі, але припускається, що ці похибки є випадковими з математичним сподіванням, що дорівнює нулю. Будемо наближати невідому функцію  за допомогою лінійної комбінації деяких відомих
за допомогою лінійної комбінації деяких відомих 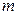 функцій
функцій 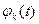
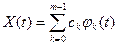 , (5.39)
, (5.39)
де функції  ,
,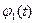 , . . .,
, . . ., називатимемо базовими функціями. Потрібно визначити
називатимемо базовими функціями. Потрібно визначити 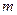 невідомих коефіцієнтів
невідомих коефіцієнтів  (
(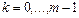 ) з умови, щоб квадрат середньоквадратичного відхилення (СКВ) апроксимуючої функції
) з умови, щоб квадрат середньоквадратичного відхилення (СКВ) апроксимуючої функції  від апроксимованої
від апроксимованої  (обчисленого для заданих значень
(обчисленого для заданих значень  аргумента
аргумента  )
)
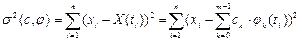 (5.40)
(5.40)
був мінімальним (саме тому відповідний метод називається МНК). Квадрат СКВ (5.40) є функцією 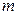 невідомих коефіцієнтів
невідомих коефіцієнтів  (
(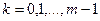 ). Тому для пошуку його мінімуму необхідно знайти
). Тому для пошуку його мінімуму необхідно знайти 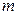 частинних похідних за окремими коефіцієнтами
частинних похідних за окремими коефіцієнтами
 (5.41)
(5.41)
і прирівняти їх до нуля. В результаті одержується система з  лінійних алгебричних рівнянь з
лінійних алгебричних рівнянь з 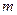 невідомими
невідомими  ,
,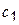 ,...,
,..., :
:
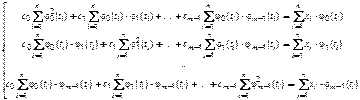 (5.42)
(5.42)
Система (5.42) називається нормальною системою для методу найменших квадратів. Визначником цієї системи є визначник Грама сукупності функцій  :
:
 (5.43)
(5.43)
Як відомо, якщо функції 
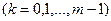 складають сукупність взаємонезалежних функцій (тобто ніяку з цих функцій неможливо подати як лінійну комбінацію решти з них), то визначник Грама цих функцій не дорівнює нулю. Це означає, що за базові функції при апроксимуванні потрібно обирати сукупності лінійно незалежних функцій. Тоді СЛАР (5.42) має єдиний розв'язок - значення коефіцієнтів
складають сукупність взаємонезалежних функцій (тобто ніяку з цих функцій неможливо подати як лінійну комбінацію решти з них), то визначник Грама цих функцій не дорівнює нулю. Це означає, що за базові функції при апроксимуванні потрібно обирати сукупності лінійно незалежних функцій. Тоді СЛАР (5.42) має єдиний розв'язок - значення коефіцієнтів 
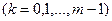 , що забезпечують мінімум квадрата середньоквадратичного відхилення апроксимуючої та апроксимованої функцій.
, що забезпечують мінімум квадрата середньоквадратичного відхилення апроксимуючої та апроксимованої функцій.
Ортогональними на деякому інтервалі 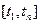 функціями називається сукупність таких функцій, що
функціями називається сукупність таких функцій, що
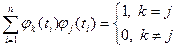 .
.
Матриця Грама для ортогональних функцій є одиничною.
У випадку, коли за базові при апроксимуванні обрані ортогональні функції, обчислення коефіцієнтів апроксимації значно спрощується. У цьому випадку значення їх можна визначити співвідношенням
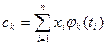 . (5.44)
. (5.44)
Тому при апроксимуванні бажано обирати за базові системи ортогональних функцій.
Класичними прикладами ортогональних функцій-поліномів є поліноми Якобі, Лежандра, Лагерра, Чебишева, Ерміта. Наприклад, поліноми Лежандра  є ортогональними на відрізку
є ортогональними на відрізку 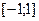 і мають вигляд:
і мають вигляд:

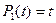 ;
;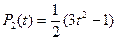 ;
;
 ;
;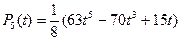 ;
;
 ;
;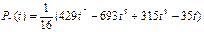 .
.
Поліноми Чебишева першого роду  є ортогональними також на інтервалі
є ортогональними також на інтервалі 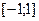 . Їх можна задати співвідношенням
. Їх можна задати співвідношенням
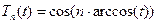 ;
; 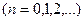 ,
,
а рекурентна формула їх визначення має такий вигляд:
 ;
; 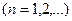 .
.
Наведемо приклади поліномів Чебишева першого роду:

 ;
; ;
; ;
;
 ;
;  ;
;
 ;
; 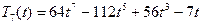 .
.
Поліноми Чебишева другого роду  також ортогональні на тому самому інтервалі і мають такий вигляд:
також ортогональні на тому самому інтервалі і мають такий вигляд:
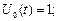
 ;
; ;
; ;
;
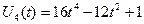 ;
; 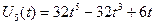 .
.
Поліноми Ерміта 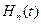 ортогональні на всій числовій осі
ортогональні на всій числовій осі  і мають вигляд
і мають вигляд
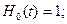
 ;
;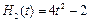 ;
; ;
;
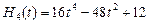 ;
;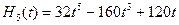 .
.
Наведені системи ортогональних поліномів стають у нагоді, коли за апроксимуючу функцію обирається поліном певного степеня, тобто для здійснення так званої поліноміальної апроксимації.
Прикладом системи неортогональних базових поліномів може бути така система:
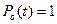 ;
; 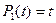 ;...,
;..., ;....
;....
Вона часто використовується на практиці. Тоді  - многочлен степеня
- многочлен степеня 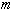 . В цьому разі до розв’язку пропонується система вигляду
. В цьому разі до розв’язку пропонується система вигляду

При 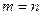 отриманий многочлен збігається з інтерполяційним многочленом Лагранжа.
отриманий многочлен збігається з інтерполяційним многочленом Лагранжа.
Приклад. Найпростіша емпірична формула  .
.
Про придатність цієї формули можна робити висновки за величинами  . Якщо
. Якщо 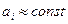 , то формула підходить. Невідомі коефіцієнти
, то формула підходить. Невідомі коефіцієнти  знайдемо з необхідної умови екстремуму функції
знайдемо з необхідної умови екстремуму функції
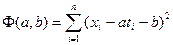 .
.
У результаті одержимо систему лінійних рівнянь
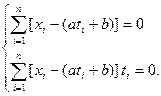
Розв’язуючи систему ,знаходимо a і b , що при заданому вигляді рівняння регресії забезпечують мінімум  (a,b) .
(a,b) .
a= ; b=
; b=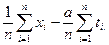
При цьому, природно, у результаті апроксимування певної сукупності даних в усіх випадках одержується однаковий поліном. Різниця полягає лише у зручності, простоті отримання коефіцієнтів цього полінома.
Якщо при поліноміальній апроксимації кількість базових функцій-поліномів дорівнює 2, тобто 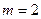 , апроксимація називається лінійною. В результаті лінійного апроксимування одержують так звану лінію регресії (пряму). При
, апроксимація називається лінійною. В результаті лінійного апроксимування одержують так звану лінію регресії (пряму). При  апроксимування називають квадратичним, а при
апроксимування називають квадратичним, а при  -кубічним.
-кубічним.
Звичайно, апроксимування не обов'язково має бути поліноміальним. Наприклад, якщо відомо, що вимірювана функція є періодичною з відомим періодом  , де
, де  - кругова частота, то за базові функції зручно використовувати таку сукупність:
- кругова частота, то за базові функції зручно використовувати таку сукупність:
 ;
;  ;
; 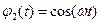 ; . . .,
; . . .,
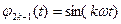 ;
;  ; . . . ,
; . . . ,
тобто використовувати апроксимацію у вигляді ряду Фур'є. Тут 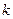 є цілим додатним числом, яке дорівнює номеру гармоніки у розкладі Фур'є.
є цілим додатним числом, яке дорівнює номеру гармоніки у розкладі Фур'є.
Наведена сукупність функцій є ортогональною на інтервалі, кратному періодові 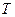 . Тому застосування її є вельми ефективним (потребує мінімуму обчислень), якщо інтервал вимірювання обрати кратним періодові.
. Тому застосування її є вельми ефективним (потребує мінімуму обчислень), якщо інтервал вимірювання обрати кратним періодові.
Опис результатів спостережень методом найменших квадратів ускладнюється, якщо невідомі коефіцієнти в рівняння регресії входять нелінійно. Однак у багатьох випадках задачу вдається спростити, застосовуючи деякі прості перетворення вихідного рівняння регресії.
Приклад.У ряді випадків до лінійної залежності можуть бути зведені експериментальні дані, коли їхній графік у декартовій системі координат не є пряма. Цього можна досягти шляхом уведення нових змінних 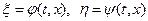 , які вибираються так, щоб точки
, які вибираються так, щоб точки  лежали на прямій. Таке перетворення називається вирівнюванням даних. Наприклад, рівняння регресії має вигляд х=ce
лежали на прямій. Таке перетворення називається вирівнюванням даних. Наприклад, рівняння регресії має вигляд х=ce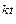 . Прологарифмуємо функцію lnх=lnc+kt. Позначимо lnx=z, lnc=a. В результаті одержуємо лінійне рівняння z=a+kt. Методом найменших квадратів знаходимо значення а і k (див. приклад вище), після чого визначимо так само c=e
. Прологарифмуємо функцію lnх=lnc+kt. Позначимо lnx=z, lnc=a. В результаті одержуємо лінійне рівняння z=a+kt. Методом найменших квадратів знаходимо значення а і k (див. приклад вище), після чого визначимо так само c=e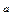
Вибір вигляду регресійної залежності можна здійснити за таблицею. Для цього за вихідними даними обчислюють середні значення хср та уср
 ,
,  ,
,  ,
,
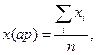
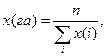
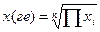 .
.
Величина обчислюється в такий спосіб:
обчислюється в такий спосіб:
1) якщо  збігається з одним із вихідних
збігається з одним із вихідних  , то
, то  ;
;
2) якщо  знаходиться між
знаходиться між  і
і  , то
, то  знаходимо як ординату відповідної точки на відрізку прямої, що з'єднує вузли
знаходимо як ординату відповідної точки на відрізку прямої, що з'єднує вузли  і
і , за формулою
, за формулою
 .
.
Вибір рівняння регресії здійснюється шляхом пошуку мінімального значення виразу 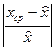 і відповідної йому функції, використовуючи таблицю.
і відповідної йому функції, використовуючи таблицю.
Таблиця 5.1 Вибір залежності
| N | .
| 
| 
| 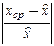
| Вигляд функції | |
| t(ар) | x(ар) | x=а0+a1*t | ||||
| t(га) | x(ар) | x=а0+а1 /t | ||||
| t(ге) | x(ар) | x=a0+a1 lg t | ||||
| t(ар) | x(ге) | x=a0*a1t | ||||
| t(ге) | x(ге) | x=a0*ta1 | ||||
| t(га) | x(ге) | x=exp(a0+a1 /t) | ||||
| t(ар) | x(га) | x=1/(a0+a1*t) | ||||
| t(ге) | x(га) | x=1/(a0+a1 lg t) | ||||
| t(га) | x(га) | x=t/(a0+a1*t) | ||||
Таблицею доречно користуватися, якщо значення нашої функції носять монотонний характер.
Приклад. Функція y=f(x) задана таблицею значень  у точках
у точках  . Використовуючи метод найменших квадратів (МНК), знайти многочлен
. Використовуючи метод найменших квадратів (МНК), знайти многочлен  найкращого середньоквадратичного наближення оптимального степеня m=m*. За оптимальне значення m* прийняти той степінь многочлена, починаючи з якого
найкращого середньоквадратичного наближення оптимального степеня m=m*. За оптимальне значення m* прийняти той степінь многочлена, починаючи з якого  стабілізується або починає зростати.
стабілізується або починає зростати.
Порядок розв’зання задачі:
1 Задати вектори x та y вихідних даних.
2 Використовуючи функціюmnk , знайти многочлени Pm, m=0,1,2,..., за методом найменших квадратів. Обчислити відповідні їм значення  .
.
3 Побудувати гістограму залежності  від m, на підставі якої вибрати оптимальний степінь m* многочлена найкращого середньоквадратичного наближення.
від m, на підставі якої вибрати оптимальний степінь m* многочлена найкращого середньоквадратичного наближення.
4 На одному кресленні побудувати графіки многочленів Pm, m=0,1,2,..., m* і точковий графік вихідної функції.
Вектори вихідних даних:
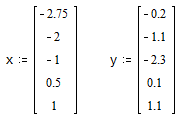 Функція mnk, що будує многочлен степеня m за методом найменших квадратів, повертає векторa коефіцієнтів многочлена:
Функція mnk, що будує многочлен степеня m за методом найменших квадратів, повертає векторa коефіцієнтів многочлена:
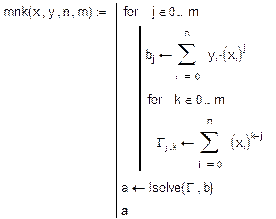
- формуються вектор правих частин та матриця нормальної системи Гa=b методу найменших квадратів (базисні функції - 1, x, ,х2...,хm);
- lsolve(Г,b) – вбудована функція MATHCAD, що розв’язує систему лінійних алгебраїчних рівнянь .
Вхідні параметри:
x, y - вектори вихідних даних; n+1 - розмірність x,y.
Обчислення коефіцієнтів многочленів степеня 0,1,2,3 за методом найменших квадратів: 


Функція P повертає значення многочлена степеня m у точці t; многочлен задається за допомогою вектора коефіцієнтів a: 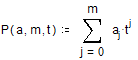
Функція 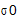 повертає значення середньоквадратичного відхилення многочлена P(a,m,t):
повертає значення середньоквадратичного відхилення многочлена P(a,m,t):
|
Обчислення значень 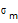 ,m=0,1,2,3:
,m=0,1,2,3: 
Гістограма
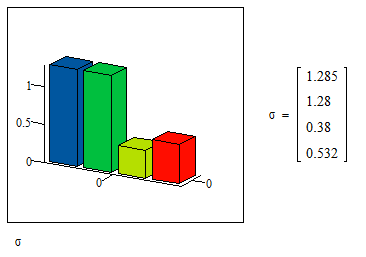
Висновок: оптимальний степінь m*=2; многочлен найкращого середньоквадратичного наближення: P2(x)=-1.102+1.598x+0.717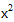
Графіки многочленів степеня 0,1,2 і точковий графік вихідної функції:
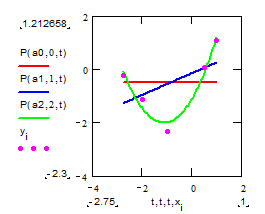
Прикладреалізації методу найменших квадратів на псевдокоді.
Нехай за допомогою зазначеного вище методу ми знайшли вигляд рівняння регресії
 , отже
, отже  .
.
Значення невідомих коефіцієнтів
 .
.
Очевидно, що процедура, яка знайде розв’язки, буде простішою, якщо ми домовимося, що функції, що обчислюють відповідні суми, нами вже реалізовані:
//обчислення коефіцієнтів регресійної формули.
//X,Y – задані в умові масиви; a1,a0 – шукані коефіцієнти
//n – кількість заданих пар x,y в умові
Metod_Kvadr(n,X,Y,a1,a0):
1 a1:=(yixi(X,Y,n)-1/N)*yi(Y,n)*yi_na_1(X,n))/(yi_na_1_kw(X,n)-(1/n)*pow(yi_na_1(X,n),2));
2 a0:=(1./n)*(yi(Y,n)-a1*yi_na_1(X,n));
End
Питання і завдання до розділу 5
1 Постановка задач наближення функцій.
2 Метод найменших квадратів. Виведення нормальної системи методу найменших квадратів.
3 Обумовленість нормальної системи.
4 Вибір оптимального степеня апроксимуючого многочлена.
5 Поліноміальна інтерполяція. Многочлен у формі Лагранжа.
6 Многочлен у формі Ньютона.
7 Похибка інтерполяції.
8 Глобальна інтерполяція. Кусочно-поліноміальна інтерполяція. Вибір вузлів інтерполяції.
9 Інтерполяція із кратними вузлами.
10 Мінімізація оцінки похибки інтерполяції.
11 Інтерполяція сплайнами. Визначення сплайна. Лінійний сплайн.
12 Побудова кубічного сплайна.
13 Види граничних умов при побудові сплайнів.
14 обудова параболічного сплайна.
15 нтерполяція функції двох змінних.
16 Вивести нормальну систему методу найменших квадратів для визначення коефіцієнтів 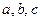 функції:
функції:
a)  ; b)
; b) 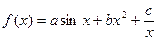 .
.
17 Використовуючи метод найменших квадратів, апроксимувати на відрізку  функцію
функцію 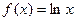 многочленом першого степеня. Обчислити величину середньоквадратичного відхилення.
многочленом першого степеня. Обчислити величину середньоквадратичного відхилення.
18 Побудувати інтерполяційний многочлен у формі Лагранжа й у формі Ньютона для функції  , заданої таблицею значень.
, заданої таблицею значень.
| a) | x | -1 | b) | x | |||||
| y | y |
19 Обчислити 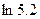 , знаючи значення
, знаючи значення  та
та 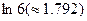 .
.
20 Побудувати кусково-лінійну інтерполяцію функції 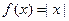 за вузлами –1, 0, 1.
за вузлами –1, 0, 1.
21 Функція  наближається на відрізку
наближається на відрізку 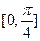 інтерполяційним многочленом за значеннями в точках
інтерполяційним многочленом за значеннями в точках 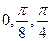 . Оцінити похибку інтерполяції на цьому відрізку.
. Оцінити похибку інтерполяції на цьому відрізку.
22 З яким постійним кроком h потрібно скласти таблицю функції  на відрізку
на відрізку 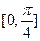 , щоб похибка лінійної інтерполяції не перевищувала
, щоб похибка лінійної інтерполяції не перевищувала 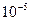 ?
?
23 Для таблично заданих функцій
| a) | x | -1 | b) | x | |||||||
| y | y |
побудувати лінійний і параболічний сплайни.
24 Функція y=y(x) задана таблицею своїх значень:
| x | -1 | |||
| y | 1.8 | 2.4 | 2.2 |
Побудувати многочлени нульового й першого степенів, що наближають функцію за методом найменших квадратів. Обчислити величину середньоквадратичного відхилення. Побудувати на одному кресленні точковий графік функції й графіки многочленів.
25 Побудувати інтерполяційні многочлени у формі Лагранжа й Ньютона, що наближають функцію y=y(x), задану таблицею своїх значень. Порівняти результати.
| x | |||
| y |
26 Функція у=y(x) задана таблицею своїх значень:
| x | 0.2 | 0.4 | 0.6 | 0.8 | ||
| y | 0.75 | 1.1 | 1.35 | 1.25 | 1.05 | 0.8 |
Запропонувати способи інтерполяції для знаходження значень функції в точках x=0.24,0.5, 0.96.
27 Відновити многочлен  за його значеннями:
за його значеннями:

| |||

|
28 Функція  задана таблицею своїх значень:
задана таблицею своїх значень:

| ||||
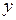
|
Обчислити наближено значення функції в точці 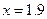 за допомогою інтерполяційного многочлена другого ступеня: а) у формі Лагранжа; б) у формі Ньютона (зі скінченними різницями). Оцінити похибку інтерполяції.
за допомогою інтерполяційного многочлена другого ступеня: а) у формі Лагранжа; б) у формі Ньютона (зі скінченними різницями). Оцінити похибку інтерполяції.
29 Функція 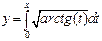 задана таблицею своїх значень:
задана таблицею своїх значень:

| 0.6 | 0.8 | 1.0 | 1.2 | 1.4 |
| 0.302 | 0.458 | 0.629 | 0.811 | 1.002 |
Обчислити приблизно значення функції в точці  за допомогою інтерполяційного многочлена у формі Ньютона (з розділеними різницями). Обчислити похибку інтерполяції.
за допомогою інтерполяційного многочлена у формі Ньютона (з розділеними різницями). Обчислити похибку інтерполяції.
30 Функція  задана таблицею своїх значень:
задана таблицею своїх значень:

| |||
|
Побудувати природний інтерполяційний кубічний сплайн дефекту 1.
31 Відомо, що апроксимуюча функція має вигляд  , де a й b – невідомі параметри. Використовуючи метод найменших квадратів, визначити a й b, якщо відомо таблицю значень функції:
, де a й b – невідомі параметри. Використовуючи метод найменших квадратів, визначити a й b, якщо відомо таблицю значень функції:

| 0.1 | 0.2 | 0.5 |
| 10.22 | 5.14 | 2.76 |
32 Вивести систему рівнянь для визначення коефіцієнтів a й b функції 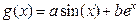 , що здійснює середньоквадратичну апроксимацію таблично заданої функції y(x) в n+1 точках.
, що здійснює середньоквадратичну апроксимацію таблично заданої функції y(x) в n+1 точках.
33 Функція  наближається інтерполяційним многочленом за значеннями в точках x=0,
наближається інтерполяційним многочленом за значеннями в точках x=0, ,
, . Оцінити похибку інтерполяції на відрізку
. Оцінити похибку інтерполяції на відрізку 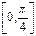 .
.
34 З яким кроком варто задати таблицю логарифмів на відрізку [1,10], щоб при квадратичній інтерполяції значення в проміжній точці відновлювалося з похибкою 0.001?
Розділ 6
Чисельне диференціювання
Чисельне диференціювання застосовується, якщо функцію f(x) важко чи неможливо продиференціювати, наприклад, якщо вона задана таблично. Воно також необхідне при розв’язанні диференціальних рівнянь за допомогою різницевих методів. Якщо маємо явний вигляд функції, то вираз для похідної часто виявляється досить складним і бажано його замінити більш простим. Якщо ж функція задана тільки в деяких точках (таблично), то одержати явний вигляд її похідних взагалі неможливо. У цих ситуаціях виникає необхідність наближеного (чисельного) диференціювання.
При чисельному диференціюванні функцію f(x) апроксимують функцією  , що легко обчислюється, і вважають, що у'(x)=
, що легко обчислюється, і вважають, що у'(x)=  . При цьому можна використовувати різні способи апроксимації. Розглянемо найпростіший спосіб – апроксимацію інтерполяційним многочленом Ньютона.
. При цьому можна використовувати різні способи апроксимації. Розглянемо найпростіший спосіб – апроксимацію інтерполяційним многочленом Ньютона.
Щоб побудувати формули чисельного диференціювання, задану на відрізку [a; b ] функцію  замінюють відповідним інтерполяційним многочленом Р(х). Tоді
замінюють відповідним інтерполяційним многочленом Р(х). Tоді
f(x)=P(x) + R(x;f), (6.1)
де R(x;f) — залишковий член інтерполяційної формули. Якщо функція 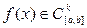 , то, диференціюючи (6.1), знаходимо
, то, диференціюючи (6.1), знаходимо
f'(х) =Р'(х) + R'(x,f),
f'' (х) =Р''(х) + R'' (x,f),
……………………….
f(k)(x)=P(k)(x)+R(k)(x;f).
Звідси отримуємо наближення
f' (x) ≈ P'(x), f''(x) ≈ Р''(х),...., f(k)(x)= P(k)(x), (6.2)
Тоді залишкові члени ri(х) (i=1,2, ... , k) формул чисельного диференціювання (6.2) дорівнюватимуть похідним від залишкового члена інтерполяційної формули (6.1), тобто
ri(х)= f(і)(х)- Р(і)(х). (6.3)
Варто зазначити, що з малості залишкового члена інтерполяційної формули R(x;f) зовсім не випливає малість залишкових членів похідних (похибки чисельного диференціювання) ri(х), бо похідні від малих функцій можуть бути досить великими. Наприклад, функції y1(x)=f(x) i y2(х)= f(x) +  для великих значень n можуть відрізнятися між собою як завгодно мало
для великих значень n можуть відрізнятися між собою як завгодно мало 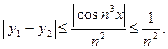
Але похідні від них для деяких значень х i великих значень п можуть значно відрізнятися між собою:
 ,
,
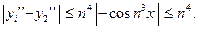
Звідси бачимо, що не існує неперервної залежності значень похідної від значень функції. Тому задача чисельного диференціювання, загалом кажучи, - менш точна операція порівняно з інтерполюванням і є некоректною задачею.

Рис. – 6.1.
На рис. 6.1 в точці x1 ординати функції f i многочлена Р однакові, проте кутові коефіцієнти дотичних значно відрізняються.
Якщо інтерполяційний многочлен Р на певній ділянці з достатньою точністю наближає функцію f, а сама функція f досить гладка i змінюється плавно на цій ділянці, то можна сподіватися, що при досить малому кроці інтерполювання похідні інтерполяційного многочлена також мало відрізнятимуться від похідних функції f. Проте не варто забувати, що зі зростанням порядку похідної точність чисельного диференціювання здебільшого різко спадає. Тому на практиці формули чисельного диференціювання для похідних, вищих від другого порядку, застосовують досить рідко.
Отже, функцію  треба продиференціювати кілька разів і знайти ці похідні в деякій точці.
треба продиференціювати кілька разів і знайти ці похідні в деякій точці.
6.1 Формули чисельного диференціювання
Розглянемо найпростіші формули чисельного диференціювання, що виводяться зазначеним способом.
Зупинимося на функції, що задана в рівновіддалених вузлах  . Її значення і значення похідних у вузлах будемо позначати
. Її значення і значення похідних у вузлах будемо позначати 
Нехай функція задана в двох точках  і
і 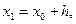 її значеннями є
її значеннями є 
Побудуємо інтерполяційний многочлен першого степеня  Похідна
Похідна 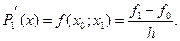

Похідну функції  в точці
в точці 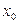 приблизно заміняємо похідною інтерполяційного многочлена
приблизно заміняємо похідною інтерполяційного многочлена
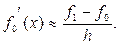 (6.4)
(6.4)
Величина 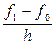 називається першою різницевою похідною.
називається першою різницевою похідною.
Нехай тепер  задана в трьох точках
задана в трьох точках 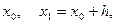
 Інтерполяційний многочлен Ньютона другого степеня має вигляд
Інтерполяційний многочлен Ньютона другого степеня має вигляд
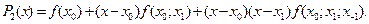
Тоді 

Одержуємо наближену формулу
 (6.5)
(6.5)
Величина 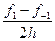 називається центральною різницевою похідною. Нарешті, для другої похідної
називається центральною різницевою похідною. Нарешті, для другої похідної
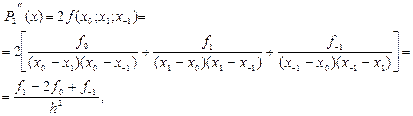 одержуємо наближену формулу
одержуємо наближену формулу
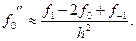 (6.6)
(6.6)
Величина  називається другою різницевою похідною.
називається другою різницевою похідною.
Формули (6.4)-(6.6) називаються формулами чисельного диференціювання.
Вважаючи функцію 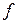 достатнє число разів неперервно диференційованою, одержимо похибки наближених формул (6.4)-(6.6). Надалі нам знадобляться такі леми.
достатнє число разів неперервно диференційованою, одержимо похибки наближених формул (6.4)-(6.6). Надалі нам знадобляться такі леми.
Лема 1 Нехай  довільні точки,
довільні точки,  Тоді існує така точка
Тоді існує така точка  що
що
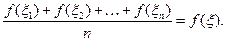
Доведення. Очевидна нерівність
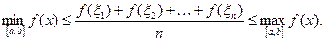
За теоремою Больцано-Коши про проміжні значення неперервної функції на замкненому відрізку, вона набуває всіх значень між 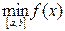 і
і 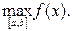 Значить, існує така точка
Значить, існує така точка 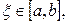 що стверджує зазначену в лемі рівність.
що стверджує зазначену в лемі рівність.
Лема 2
1 Припустимо, що 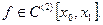 Тоді існує така точка
Тоді існує така точка 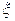 , що
, що
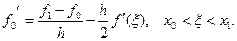 (6.7)
(6.7)
2 Якщо 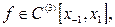 то є така точка
то є така точка 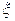 , що
, що
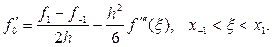 (6.8)
(6.8)
3 Коли 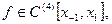 то є точка
то є точка  така, що
така, що
 (6.9)
(6.9)
Доведення.Розглянемо розкладання Доведення. За формулою Тейлора

звідки випливає (6.4). Якщо 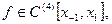 то за формулою Тейлора
то за формулою Тейлора
 (6.10)
(6.10)
де 
Підставимо (6.10) у вираз  Одержимо
Одержимо
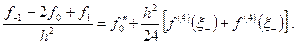
Заміняючи відповідно до леми 1

одержуємо 
Звідки і випливає (6.9). Рівність (6.8) доводиться аналогічно. Формули (6.4)-(6.6) називаються формулами чисельного диференціювання із залишковими членами.
Похибки формул (6.4)-(6.6) оцінюються за допомогою наступних нерівностей, що випливають із співвідношень (6.7)-(6.9):
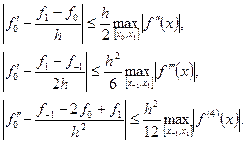
Вважають, що похибка формули (6.4) має перший порядок відносно 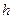 , а похибка формул (6.5) і (6.6) другого порядку відносно
, а похибка формул (6.5) і (6.6) другого порядку відносно 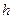 (чи порядку
(чи порядку 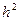 ). Також говорять, що формула чисельного диференціювання (6.4) першого порядку точності (відносно
). Також говорять, що формула чисельного диференціювання (6.4) першого порядку точності (відносно 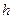 ), а формули (6.5) і (6.6) мають другий порядок точності.
), а формули (6.5) і (6.6) мають другий порядок точності.
Зазначеним способом можна одержувати формули чисельного диференціювання для старших похідних і для більшої кількості вузлів інтерполяції.
Для вибору оптимального кроку припустимо, що границя абсолютної похибки при обчисленні функції 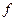 в кожній точці задовольняє нерівність
в кожній точці задовольняє нерівність
 (6.11)
(6.11)
Нехай у деякому околі точки  похідні, через які виражаються залишкові члени у формулах (6.8), (6.9), неперервні і задовольняють нерівності
похідні, через які виражаються залишкові члени у формулах (6.8), (6.9), неперервні і задовольняють нерівності
 (6.12)
(6.12)
де 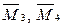 - деякі числа. Тоді повна похибка формул (6.5), (6.6) (без урахування похибок округлення) відповідно до (6.8), (6.9), (6.11), (6.12) не перевершує відповідно величин
- деякі числа. Тоді повна похибка формул (6.5), (6.6) (без урахування похибок округлення) відповідно до (6.8), (6.9), (6.11), (6.12) не перевершує відповідно величин
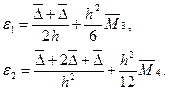
Мінімізація за 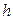 цих величин приводить до таких значень кроків:
цих величин приводить до таких значень кроків:  при цьому
при цьому
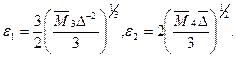 (6.13)
(6.13)
Якщо при обраному для будь-якої з формул (6.5), (6.6) значенні  відрізок
відрізок  не виходить за окіл точки
не виходить за окіл точки  , у якому виконується нерівність (6.12), то знайдене
, у якому виконується нерівність (6.12), то знайдене  є оптимальним і повна похибка чисельного диференціювання оцінюється відповідною величиною (6.13).
є оптимальним і повна похибка чисельного диференціювання оцінюється відповідною величиною (6.13).
6.2 Дослідження точності чисельного диференціювання
Дослідження точності отриманих виразів при чисельних розрахунках зручно робити за допомогою апостеріорної оцінки, за швидкістю спадання членів відповідного ряду Тейлора. Якщо крок сітки досить малий, то похибка близька до першого відкинутого члена.
У такий спосіб порядок точності результату відносно кроку сітки дорівнює числу залишених членів ряду, або, іншими словами, він дорівнює числу вузлів інтерполяції мінус порядок похідної. Тому мінімальне число вузлів необхідне для обчислення m-ої похідної, дорівнює m+1, воно забезпечує перший порядок точності.
Ці висновки відповідають принципу: при почленному диференціюванні ряду швидкість його збіжності зменшується.
Якщо врахувати погіршення збіжності ряду при диференціюванні, то можна зробити висновок: навіть якщо функція задана добре складеною таблицею на досить докладній сітці, то практично чисельним диференціюванням можна визначити першу і другу похідні, а третю і четверту – лише з великою похибкою. Похідні більш високого порядку рідко вдається обчислити із задовільною точністю.
Метод Рунге-Ромберга
Загальна ідея методу така: маємо деяку наближену формулу (х,к) для обчислення величини z(х) за її значеннями на рівномірній сітці з кроком h, а… . (6.14) Наприклад, , —задана функція. Нехай , ,Зауваження
2 Метод Ромберга можна застосувати не лише для розкладання вигляду з функціями , як в (6.18), але й для довільних функцій . Коли , що часто… , і може бути обчислений в точці за допомогою, наприклад, алгоритму Ньютона без розв'язування системи.Процес Ейткена
, але - невідоме. Проводяться обчислення на трьох сітках з кроками .End
//Повертає одну суму з формули Симпсона
//a – лівий кінець відрізка інтегрування
//h – крок
sum1(n,h,a):
1 temp:=0
2 for i:=1 to (an div 2) do
3 temp+=f(a+(2*k-1)*ah)
Done
5 return temp
End
//Повертає одну суму з формули Симпсона
//a – лівий кінець відрізка інтегрування
//h – крок
sum2(n,h,a):
1 temp:=0;
2 for k:=2 to (an div 2) do
3 temp+=f(a+(2*k-2)*ah)
Done
5 return temp
End
Calc_Integrate_Simpson(a,b,
1 n:=4
2 h:=(b-a)/n
Repeat
4 I1:=(h*(f(a)+f(b)+4*sum1(n,h,a)+2*sum2(n,h,a)))/3;
5 n:=2*n;
6 h:=(b-a)/n;
7 I2:=(h*(f(a)+f(b)+4*sum1(n,h,a)+2*sum2(n,h,a)))/3
8 m:=abs(I1-I2)
9 until (m<eps)
10 returnI2
End
Квадратурна формула Гауса
К.Ф.Гаус звернув увагу, що квадратурна формула має невідомих параметрів та , тобто саме стільки, скільки параметрів має алгебраїчний поліном степеня… Спочатку для спрощення розглянемо відрізок , тобто інтеграл вигляду (7.7)Квадратурна формула Чебишева
. (7.10) Параметри виберемо так, щоб формула була точною для всіх поліномів степеня не… Для маємоКубатурна формула типу Симпсона
, де . Усього, таким чином, одержимо точок сітки. Маємо . (7.23)Метод Ейлера
, (8.1) . (8.2) Відзначимо, що на практиці цей метод використовується рідко через невисоку точність, однак він є найпростішим з…Схеми Рунге-Кутта другого порядку
, де залишковий член . (8.9)Схеми Рунге-Кутта четвертого порядку
Так схема ламаних Ейлера (8.5) є схемою Рунне-Kyттa першого порядку точності. Найбільш уживані схеми четвертого порядку точності. Наведемо без… , ,Repeat
2 for j:=1 to 2 do
3 Y[j,1]:=BeginValue
4 for i:=1 to n do
5 x:=a+(i-1)*h
6 k1:=f(x,Y[j,i])
7 k2:=f((x+h/2),(Y[j,i]+h*k1/2))
8 k3:=f((x+h/2),(Y[j,i]+h*k2/2))
9 k4:=f((x+h),(Y[j,i]+h*k3))
10 Y[j,i+1]:=Y[j,i]+h*(k1+2*k2+2*k3+k4)/6
Done
12 if j=1 then
13 h:=h/2
14 n:=round((b-a)/h)
Fi
Done
17 maxr:=0
18 for i:=1 to 10 do
19 r:=abs(Y[1][((n*i) div 20)+1]-
20 -Y[2][((n*i) div 10)+1])/15;
21 if r>maxr then
22 maxr:=r
Fi
Done
25 if maxr<eps then
26 for i:=1 to 10 do
27 YF[i]:=Y[2][((n*i) div 10)+1]
Done
Fi
30 untilmaxr<eps
End
8.2 Багатокрокові методи
8.2.1 Метод прогнозу і корекції
Підправивши схему Ейлера в середній точці одержимо схему прогнозу
, (8.20)
де 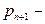 наближене значення . Використовувати формулу (8.20) не можна через те, що схема прогнозу нестійка. З цієї причини використовуємо схему корекції
наближене значення . Використовувати формулу (8.20) не можна через те, що схема прогнозу нестійка. З цієї причини використовуємо схему корекції
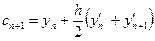 (8.21)
(8.21)
Для оцінки похибки корекції розкладемо в ряд Тейлора в околі точки корекцію
корекцію

та саму функцію 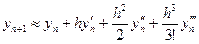 .
.
Віднявши ці два розкладання , отримаємо
 . (8.22)
. (8.22)
Для оцінки похибки прогнозу розкладемо в ряд Тейлора в околі точки прогноз
прогноз
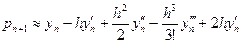 та саму функцію
та саму функцію
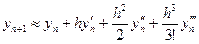 .
.
Віднявши ці два розкладання , отримаємо похибку прогнозу
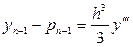 . (8.23)
. (8.23)
З цих оцінок зрозуміло, що прогноз наближає розв’язок з недостачею, а корекція з надлишком. Отже, точне значення розв’язку лежить між прогнозом і корекцією. На будь-якому кроці можна оцінити точність розв’язку . Якщо задається її значення, то 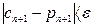 .
.
Віднімаючи рівності (8.23) та (8.22), маємо
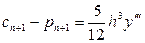 .
.
Уточнюємо розв’язок, виходячи з формули (8.22)
 . (8.24)
. (8.24)
Відтак формула (8.24) завершує схему прогнозу і корекції. .
Приклад 1 Розв’язати задачу Коші для диференціального рівняння другого порядку:
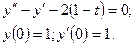
Розв’язання. 1 Введемо нові змінні :
U=y; V= . Тоді, обравши сітку
. Тоді, обравши сітку  , визначимо на ній сіткові функції
, визначимо на ній сіткові функції  :
:
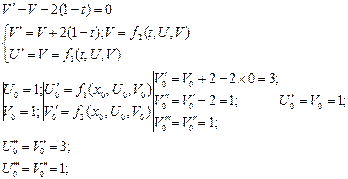
2 Знаходимо і ( ) за допомогою розкладання в ряд Тейлора :
) за допомогою розкладання в ряд Тейлора :
 3 З диференціального рівняння знаходимо
3 З диференціального рівняння знаходимо  і
і  :
:

Визначаємо прогноз розв’язку в точці 
 .
.
Тимчасово покладаючи U2=P2 ; , можна отримати
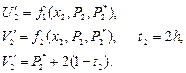
Обчислюємо корекцію  . Тепер можна визначити V2
. Тепер можна визначити V2

І нарешті на даному кроці уточнюємо розв’язок
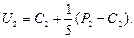
Похибка обчислення .
Приклад 2 Використовуючи метод прогнозу і корекції, реалізувати алгоритм розв’язку крайової задачі для звичайного диференціального рівняння з точністю 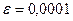 на псевдокоді.
на псевдокоді.
Розв’язання
Після заміни
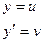
отримаємо (користуючись системою символічної математики Derive)
vo1:=-0.3-vo/(0.7)
vo2:=1-2*vo-(vo1*(0.7)-vo)/(0.7)^2
vo3:=-2*vo1-(vo2*(0.7)^3-2*(0.7)*(vo1*(0.7)-vo))/(0.7)^4
u1:=0.5+0.3*vo+vo1*(0.3)^2/2+vo2*(0.3)^3/6
(24018*vo+48307)/98000
v1:=vo+0.3*vo1+vo2*(0.3)^2/2+vo3*(0.3)^3/6
(2099500*vo-129339)/3430000
2*u1+3*v1=1.2
SOLVE(2*u1+3*v1=1.2,vo);
Simp(#9)
[vo=1122527/7979760]; Approx(#10)
[vo=5122/36411=0.140671]
тоді розв’яжемо систему:
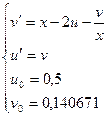
//x0 – початкове значення
//xn – кінцеве значення
//h – початковий крок
//X,Y – масиви результатів
Prognose_Correction(x0,u0,v0,h,X,Y):
1 u01:=v01;
2 v01:=x0-2*u0-v0/x0
3 u02:=v01
4 v02:=1-2*u01-((v01*x0-v0)/sqr(x0))
5 u03:=v02
6 v03:=-2*u02-((v02*x0*sqr(x0)-2*v01*sqr(x0)+2*v0*x0)/sqr(sqr(x0)))
7 u1:=u0+h*u01+h*h*u02/2+h*h*h*u03/6
8 v1:=v0+h*v01+h*h*v02/2+h*h*h*v03/6
9 i:=0
10 while (x1<=xN) do
11 i++
Repeat
13 x1:=x0+i*h
14 x2:=x0+(i+1)*h
15 v11:=x1-2*u1-v1/x1
16 u11:=v1
17 p2:=u0+2*h*u11
18 p2z:=v0+2*h*v11
19 u2:=p2
20 v2:=p2z
21 u21:=p2z
22 v21:=x2-2*p2-p2z/x2
23 c2z:=v1+h*(v11+v21)/2
24 v2:=c2z+(p2z-c2z)/5
25 u21:=v2
26 c2:=u1+h*(u11+u21)/2
27 u2:=c2+(p2-c2)/5
28 if abs(p2-c2)<eps then
29 X[i]:=x2;
30 Y[i]:=u2;
Fi
32 if abs(p2-c2)>e then
33 h:=h/2;
Fi
35 until abs(p2-c2)<eps;
36 done//while
end
Методи Адамса
На відміну від однокрокових методів, у яких числовий розв’язок одержують тільки з диференціального рівняння і початкової умови, алгоритми Адамса… Стартові значення можна одержати декількома способами. Дж. К. Адамс обчислював… Розглянемо чисельні методи розв’язання задачі Коші (8.1)-(8.2), які можуть бути задані формулою– Конец работы –
Используемые теги: Абсолютна, відносна, похибки0.09
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Абсолютна і відносна похибки
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?








Новости и инфо для студентов