Определение доверительного коэффициента

Если закон распределения неизвестен, то для оценки доверительного интервала следует воспользоваться неравенством Чебышева (не самом деле Чебышёв Пафнутий Львович (1821 – 1894), русский математик и механик)

.

В предельном случае

,

где 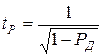– т.н. доверительный коэффициент, зависящий от доверительной вероятности.

Значения 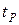, получаемые из неравенства Чебышева, оказываются чрезмерно завышенными, особенно при . Поэтому для симметричных законов распределения можно воспользоваться неравенством Кампа–Мейделя

,

откуда

.

Для известных законов распределения значения доверительного коэффициента можно найти из выражения

,

подставляя вместо соответствующие аналитические выражения для интегральной функции распределения результатов или погрешностей измерения.

Равновероятное распределение (рис. 8.1)

 

 

а) б)

Рисунок 8.1 – Плотность (а) и интегральная функция (б)

равновероятного распределения результатов и погрешностей измерений

 

Плотность распределения

Интегральная функция распределения

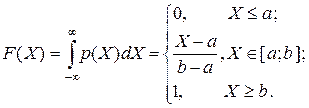
Числовые характеристики распределения:

– математическое ожидание ;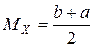

– СКО .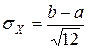

Доверительная вероятность

.

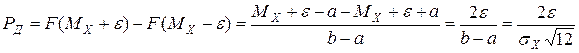Отсюда

; .

 

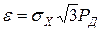Нормальное распределение (Гаусса) (рис. 8.2)

 

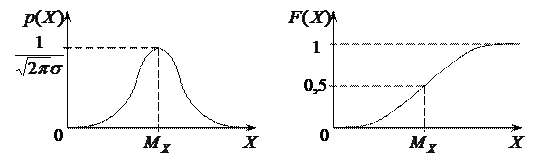а) б)

Рисунок 8.2 – Плотность (а) и интегральная функция (б)

нормального распределения результатов и погрешностей измерений

 

Плотность распределения

.

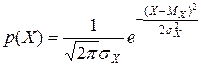Интегральная функция распределения

.

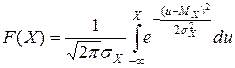Числовые характеристики распределения:

– математическое ожидание ;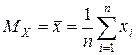

– СКО .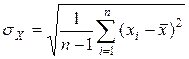

Доверительная вероятность

.

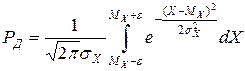Вводим замену переменного 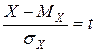, откуда 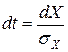и вместо в пределах интегрирования необходимо записать

,

то есть

,

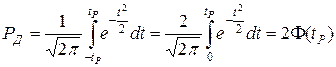где – функция Лапласа. (Пьер–Симо́н Лапла́с (1749 – 1827) – французский математик и астроном; известен работами в области небесной механики, дифференциальных уравнений, один из создателей теории вероятностей. На одном из экзаменов Лаплас высоко оценивает знания 17–летнего абитуриента Наполеона Бонапарта, впоследствии их отношения были неизменно теплыми.)

Отсюда получаем

.

Значения функции 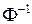, обратной функции Лапласа, табулированы.

 

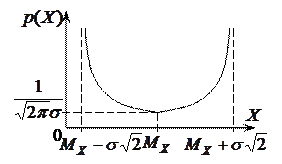
Распределение по закону арксинуса (рис. 8.3)

 

а) б)

Рисунок 8.3 – Плотность и интегральная функция

результатов и погрешностей измерений по закону арксинуса

 

Плотность распределения

Интегральная функция распределения

Числовые характеристики распределения:

– математическое ожидание ;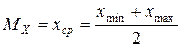

– СКО .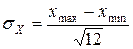

Доверительная вероятность

.

Отсюда

, .

 

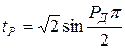Таблица 8.3 – Зависимость доверительных коэффициентов 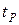от доверительной вероятности для различных законов распределения

 

Закон распределения	Доверительная вероятность
0,9	0,95	0,99	0,9973
Неравенство Чебышева	1,63	4,5
Неравенство Кампа–Мейделя	1,1		6,7
Равновероятный	1,56	1,65	1,71
Треугольный (Симпсона)	1,67	1,9	2,2
Нормальный	1,64	1,96	2,58
Лапласа	1,63	2,12	3,26	4,18
Арксинуса	1,4	1,4	1,41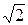