ДОСЛІДЖЕННЯ ЕЛЕКТРИЧНОГО ПОЛЯ
3.1 Мета роботи: дослідити на електролітичній моделі розподіл потенціалів в електричних полях циліндричних і плоскопаралельних електродів.
3.2 Методичні вказівки з організації самостійної роботи студентів
Силовою характеристикою електричного поля в кожній його точці є вектор напруженості , а енергетичною – потенціал
, а енергетичною – потенціал  . Графічно електричне поле будь-якої системи зарядів можна відобразити або лініями напруженості, дотичні до яких збігаються з напрямком
. Графічно електричне поле будь-якої системи зарядів можна відобразити або лініями напруженості, дотичні до яких збігаються з напрямком  , або за допомогою еквіпотенціальних поверхонь. Лінії напруженості ортогональні еквіпотенціальним поверхням у кожній точці електричного поля. Напруженість електричного поля пов’язана з потенціалом [2]:
, або за допомогою еквіпотенціальних поверхонь. Лінії напруженості ортогональні еквіпотенціальним поверхням у кожній точці електричного поля. Напруженість електричного поля пов’язана з потенціалом [2]:
 .
.
Технічно легше виконати вимірювання скалярної величини  , ніж векторної
, ніж векторної  . Для дослідження розподілу потенціалів в електричному полі використовується «точковий» електрод – зонд, який вводиться в досліджувану
. Для дослідження розподілу потенціалів в електричному полі використовується «точковий» електрод – зонд, який вводиться в досліджувану
точку поля. За допомогою зонда можна виміряти різницю потенціалів між даною та будь-якою іншою точкою електричного поля. При цьому важливо, щоб зонд не заряджався і набував потенціалу тієї точки поля, в якій він розташований.
Цю умову важко виконати в непровідному середовищі, бо зонд накопичує заряди і вони не стікають з нього. Тому дослідження електричного поля заряджених провідників замінюється дослідженням поля струмів в провідному середовищі між провідниками. Адекватність такої заміни підтверджується законом Ома в диференціальній формі
 , (3.1)
, (3.1)
де 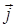 – вектор густини струму;
– вектор густини струму;
 – питомий опір провідного середовища (електроліту).
– питомий опір провідного середовища (електроліту).
Із закону Ома випливає, що в однорідному провідному середовищі лінії напруженості електричного поля збігаються за напрямком з лініями густини струмів. Тому, вимірюючи розподіл потенціалів поля густини струму в провідному середовищі, можна дослідити розподіл потенціалів електричного поля статичних зарядів. В електроліті металевий зонд не заряджається і набуває потенціалу досліджуваної точки поля, бо стікання зарядів з вістря зонду відбувається безперервно за рахунок слабкого струму, який виникає між зондом і одним із електродів. Щоб цей струм був малим і не впливав на досліджуване
поле, електричне коло зонда повинне мати значно більший опір, ніж опір електроліту.
У даній роботі в коло зонду вмикається підсилювач вертикального відхилення осцилографа з великим вхідним опором ( ), а опір електроліту на 2-3 порядки менший. Між електродами в електроліті протікає змінний синусоїдальний струм невеликої частоти (50 Гц), бо при протіканні постійного струму на електродах осідатимуть продукти розпаду, які поляризують електроди і викривлюють розподіл потенціалів досліджуваного поля.
), а опір електроліту на 2-3 порядки менший. Між електродами в електроліті протікає змінний синусоїдальний струм невеликої частоти (50 Гц), бо при протіканні постійного струму на електродах осідатимуть продукти розпаду, які поляризують електроди і викривлюють розподіл потенціалів досліджуваного поля.
3.3 Опис лабораторної установки
Лабораторна установка складається з ванни з електролітом, циліндричних та плоских електродів, точкового електроду (зонду), джерела змінної напруги, потенціометра, осцилографа, з'єднувальних дротів.
Схема установки для дослідження потенціальної картини електролітичної моделі електричного поля наведена на рис. 3.1.

Рисунок 3.1
В електролітичній ванні, заповненій електролітом, розташовані металеві електроди Е1 і Е2, електричне поле яких досліджують. На електроди подається змінна напруга ( ). У вимірювальну частину пристрою входять такі компоненти: зонд, реостат
). У вимірювальну частину пристрою входять такі компоненти: зонд, реостат  (потенціометр), осцилограф
(потенціометр), осцилограф  , який використовують як нуль-індикатор. Для вимірювання різниці потенціалів використовують вольтметр
, який використовують як нуль-індикатор. Для вимірювання різниці потенціалів використовують вольтметр 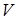 . Опір реостату між клемами 1,2 і 2,3 разом з опором електроліту між зондом і електродами утворюють електричний місток Уітстона, діагональ якого (клема 2 та зонд) містить осцилограф як нуль-індикатор. Змінюючи положення зонду по відношенню до електродів, можна знайти в електроліті такі точки поля, потенціал яких дорівнює потенціалу повзунка реостата. Наявність різниці потенціалів у діагоналі містка визначається за амплітудою вертикального відхилення на екрані осцилографа (довжина лінії). Зонд переміщуємо до того часу, доки амплітуда вертикального відхилення променя не буде мінімальною. Геометричне місце точок поля , для яких різниця потенціалів в діагоналі містка дорівнює нулю (при незмінному положенні повзунка реостата), відповідає одній з еквіпотенціальних поверхонь електричного поля. Через малу глибину ванни в досліді отримуємо не поверхню, а її горизонтальний переріз – еквіпотенціальну лінію. Змінюючи потенціал повзунка реостата, визначаємо еквіпотенціальну лінію іншої величини потенціалу. Вимірювання потенціалу повзунка реостата по відношенню до потенціалу електрода Е2 здійснюється вольтметром
. Опір реостату між клемами 1,2 і 2,3 разом з опором електроліту між зондом і електродами утворюють електричний місток Уітстона, діагональ якого (клема 2 та зонд) містить осцилограф як нуль-індикатор. Змінюючи положення зонду по відношенню до електродів, можна знайти в електроліті такі точки поля, потенціал яких дорівнює потенціалу повзунка реостата. Наявність різниці потенціалів у діагоналі містка визначається за амплітудою вертикального відхилення на екрані осцилографа (довжина лінії). Зонд переміщуємо до того часу, доки амплітуда вертикального відхилення променя не буде мінімальною. Геометричне місце точок поля , для яких різниця потенціалів в діагоналі містка дорівнює нулю (при незмінному положенні повзунка реостата), відповідає одній з еквіпотенціальних поверхонь електричного поля. Через малу глибину ванни в досліді отримуємо не поверхню, а її горизонтальний переріз – еквіпотенціальну лінію. Змінюючи потенціал повзунка реостата, визначаємо еквіпотенціальну лінію іншої величини потенціалу. Вимірювання потенціалу повзунка реостата по відношенню до потенціалу електрода Е2 здійснюється вольтметром 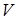 .
.
Циліндричні і плоскі електроди закріплені на підставках, де є коорди-натна сітка, за допомогою якої знаходять координати зонда, радіуси електродів та відстань між ними.
3.4 Порядок виконання роботи і методичні вказівки з її виконання
3.4.1 Дослідження електричного поля між циліндричними електродами
1. Зібрати електричну схему досліду (рис.3.1).
2. Розмістити у ванні з електролітом циліндричні електроди та зобразити їх на папері у зручному масштабі. Виміряти радіуси електродів R1 та R2.
Увімкнути живлення і виміряти різницю потенціалів j1 – j2 між електродами для розрахунку сталої k. Використати формулу зв’язку між різницею потенціалів та напруженістю електричного поля для даного досліду:
 , (3.2)
, (3.2)
де j1 та j2 – потенціали меншого та більшого електродів радіусами R1 та R2 відповідно;
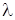 – лінійна густина заряду;
– лінійна густина заряду;
e0 – електрична стала;
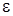 – діелектрична проникність середовища між електродами.
– діелектрична проникність середовища між електродами.
3. Вимкнути розгортку осцилографа, поставити зонд в деяке положення R між електродами і за допомогою потенціометра RП1 збалансувати плечі електричного містка, про що свідчить мінімальний розмах коливань на екрані осцилографа. Занести в таблицю даних 3.1 значення потенціалу для цього положення зонда та радіус даної еквіпотенціальної лінії. Інші положення зонда на ній знаходяться при мінімальних розмахах коливань на екрані осцилографа.
4. Для отримання даних про інші еквіпотенціальні лінії (всього 3–5 ліній) необхідно повторити завдання п.2 для інших значень радіусів (R1+1,2,3,…см).
5. Розрахувати значення jтеор(R) за формулою (3.2), де R2 = R1 +1,2,... см (за вказівкою викладача), а j1=0. Результати теоретичних та експериментальних даних занести в таблицю 3.1 та побудувати на одному рисунку залежності jтеор(R) та jексп(R) для порівняння їх між собою.
Таблиця 3.1 – Результати вимірювань та розрахунків
| R,см |  експ,В експ,В
|  теор,В теор,В
|
| R1 +1 | ||
| R1 +2 | ||
| R1 +3 |
3.4.2 Дослідження електричного поля між плоскими електродами
1. Розташувати у ванні плоскі електроди і зобразити їх у вибраному масштабі на папері.
2. Виміряти і записати відстань d між електродами. Керуючись вказівками попереднього завдання, визначити та зафіксувати на папері значення xі еквіпотенціальних ліній з відповідними їм потенціалами (3-5 ліній). Значення xі відлічувати від електроду з нульовим потенціалом. Звернути увагу на форму еквіпотенціальних ліній за межами плоских електродів. Провести на рисунку лінії напруженості електричного поля.
3. Використовуючи співвідношення для потенціалу однорідного поля, знайти значення  теор для відповідних значень х за формулою:
теор для відповідних значень х за формулою:
 .
.
Дані занести до табл.3.2.
Таблиця 3.2 – Результати вимірювань та розрахунків
| x,см |  експ, В експ, В
|  теор, В теор, В
|
| 1,0 | ||
| 2,0 | ||
| 3,0 |
4. Побудувати в одній системі координат дві залежності  – отриману експериментально
– отриману експериментально  експ та знайдену теоретично
експ та знайдену теоретично  теор. Вказати абсолютні похибки вимірів на експериментальній залежності. Порівняти отримані графіки.
теор. Вказати абсолютні похибки вимірів на експериментальній залежності. Порівняти отримані графіки.
3.5 Зміст звіту
Звіт має містити: мету роботи, схему лабораторної установки, результати вимірювань у вигляді таблиць, рисунок еквіпотенціальних ліній для циліндричних та плоских електродів, графіки залежностей  експ та
експ та  теор із зазначеними на них абсолютними похибками вимірювань, стислі висновки.
теор із зазначеними на них абсолютними похибками вимірювань, стислі висновки.
3.6 Контрольні запитання і завдання
1. Що називається напруженістю і потенціалом електричного поля?
2. Дати визначення лініям напруженості та еквіпотенціальним поверхням.
3. Чому простіше дослідити поле струмів у провідному середовищі, ніж поле статичних зарядів?
4. На основі чого вивчення поля статичних зарядів замінюється вивченням поля струмів в провідному середовищі?
5. Навіщо на електроди експериментального пристрою (рис.3.1) подається змінна напруга?
6. Пояснити принцип дії експериментального пристрою.
7. Вивести формулу для визначення потенціалів циліндричного та плоского конденсаторів.