Теорема 1. Число розміщень з n елементів по m елементів дорівнює добутку m послідовних натуральних чисел від n до n-m+1 включно, тобто
= n(n-1) (n-2) … (n-m+1), m>0(1)
Доведення. Число розміщень з n елементів по m елементів дорівнює числу всіх m-елементних упорядкованих підмножин n-елементної множини. Перший елемент підмножини можна вибрати n способами. Другий елемент підмножини можна вибрати n-1 способами, оскільки другим елементом можна взяти будь-який елемент множини, крім уже вибраного першим. Кожний із способів вибору першого елемента може об'єднуватись з кожним із способів вибору другого, тому існує n(n-1) способів вибору перших двох елементів для n-елементної упорядкованої підмножини.
Після вибору перших двох елементів залишається n-2 можливостей вибору третього елемента, і знову, як і раніше, кожна а цих можливостей може комбінуватись з будь-якою із можливостей вибору перших двох елементів, тобто вибір перших трьох елементів можна здійснити n(n-1)(n-2) способами і т.д.
Останній m-й елемент m-елементної упорядкованої підмножини n-елементної множини можна вибрати n-m+1 способом, оскільки до вибору m-го елемента залишилось n-(m-1) елементів.
Отже, число розміщень з n елементів по m елементів дорівнює
= n(n-1) (n-2) … (n-m+1),
що й треба довести.
Цю теорему можна довести Іншими способами, зокрема методом математичної індукції.
Формулу (1) можна записати в іншому вигляді, використовуючи поняття n-факторіала. Дійсно, домножимо і розділимо добуток, що стоїть у правій частині формули (1), на (n-m)!
Дістанемо
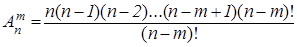
або 
(2)
Формула (2) має деякі переваги перед формулою (1) у практичному використанні.
Формула (1) виводилась у припущенні, що m>0, а формулою (2) можна користуватись і при m=0, оскільки вона і в цьому випадку дає вірний результат:
Нагадаємо, що 
=1, а порожня множина є єдиною підмножиною будь-якої множини.
При виведенні формули (1) також припускалось, що n¹0, тобто, що дана множина не порожня. Якщо n=0, то розглядається порожня множина. Оскільки порожня множина має тільки одну підмножину (саму себе), то
=1
Враховуючи, що 0!=1, то формула (2) дає вірний результат і при n=0:
Приклад 1. Розклад одного дня містить 5 різних пар. Знайти кількість можливих розкладів, якщо вивчається 9 дисциплін.
Розв'язання. Маємо розміщення з 9 елементів по 5 без повторень, їх кількість дорівнює
=9×8×7×6×5=15120
Відповідь. 15120.
У розміщеннях без повторень не має однакових елементів у виборці: після вибору першого елемента для вибору другого елемента залишається на одиницю менше можливостей i т.д.