Рассмотрим некоторые из названных и другие величины

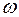Угловая скорость - вектор, численно равный dj / dt и направленный по оси вращения по правилу правого винта (если рукоятку правого винта вращать по направлению вращения тела, то направление поступательного движения винта покажет направление угловой скорости). Единицей измерения является [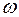] = 1 рад/с (с-1). Если вращение происходит с постоянной угловой скоростью (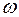=const), то 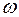=(j -j0)/t, отсюда j = j0 + 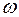t. Угловую скорость можно выразить следующим образом: 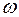= 2p / T = 2pn, где n=1/T - число оборотов в секунду, Т- период вращения.

При изменении угловой скорости вводят понятие углового ускорения:

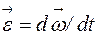[e] = 1 рад/с2 (1/с2).

Угловое ускорение - вектор, совпадающий по направлению с угловой скоростью при ускоренном движении и противоположной ей – при замедленном. Угловое ускорение связано с тангенциальным (касательным) ускорением :

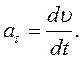
Т.к. 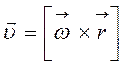, то ,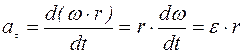

где 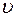- линейная скорость

Для характеристики динамики вращательного движения вводятся понятия момента силы и момента инерции.

Рассмотри движение материальной точки "А" с массой m по окружности радиусом r (рис. 1). Пусть на точку "А" массой m действует сила 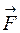, лежащая в плоскости, перпендикулярной оси вращения О. Тогда точка приобретает постоянное тангенциальное ускорение аt, определяемое тангенциальной составляющей силы :

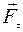Ft = F Sina = m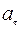 (1)

Так как = re. Равенство (1) можно записать следующим образом:

F Sina = mre (2)

Умножив правую и левую часть равенства (2) на r получим:

Fr Sina = mr2e или M =Je , отсюда:

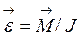, (3)

где М=FrSina или в векторной форме: 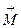= [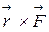] - вращающий момент (момент силы 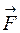), J=mr2 - момент инерции вращения материальной точки А массой m относительно оси «О».

 

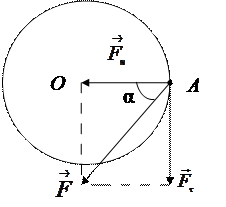
Рисунок 1. Вращение материальной точки А массой m относительно оси «О»

Зависимость 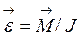является вторым законом Ньютона для вращательного движения и называется основным уравнением динамики вращательного движения. Это же выражение справедливо и для характеристики вращательного движения твердого тела с учетом того, что J - момент инерции тела, характеризующий его инерционное свойство во вращательном движении относительно какой-либо оси. Для определения момента инерции твердого тела необходимо разбить тело на бесконечно малые элементы с массой dm, найти моменты инерции каждого элемента dJ и проинтегрировать их. Каждый элемент можно приближенно принять за материальную точку c 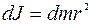, тогда:

 

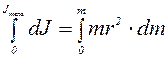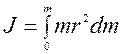или (4)

 

Для тел различной геометрической формы момент инерции рассчитывается по формулам, полученных при интегрировании выражения (4).

Для примера рассчитаем момент инерции однородного стержня длиной l и массой m, когда ось вращения ОО проходит через его середину

 

 

O

           
   
dx
 
   
 
 


x

 


Рисунок 2. Момент инерции тонкого прямого стержня

относительно его центральной оси, перпендикулярной к стержню

На расстоянии х от оси вращения выделяем малый участок стержня длиной dx масса этого участка равна dm, тогда согласно формуле (4), момент инерции для этого участка запишется в виде

 

 

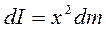
Для определения dm вводим линейную плотность, как , тогда 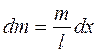, а момент инерции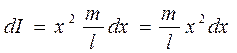

Момент инерции для всего стержня запишется в виде:

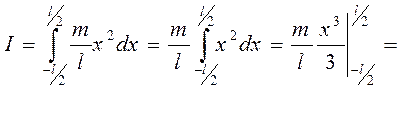
Если ось вращения тела О1О1 параллельна оси симметрии ОО, но смещена от нее на расстояние d, то момент инерции I, относительно новой оси О1О1определяется по теореме Штейнера

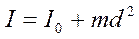
где I0 - момент инерции тела относительно оси симметрии. рассчитаем момент инерции для однородного тонкого стержня длиной l и массой m, когда ось вращения проходит перпендикулярно к стержню через его конец

;

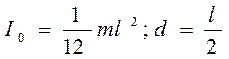тогда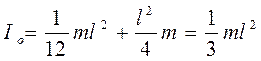

 

 

       
 
O1
 
 
 
O1
 

 


Рисунок 3. Момент инерции тонкого прямого стержня относительно оси.

 

Для других однородных тел геометрически правильной формы массой m относительно оси симметрии момент инерции рассчитывается по формулам:

1)для однородного сплошного цилиндра (диска) относительно продольной оси J=mR2/2, где m - масса цилиндра, R - его радиус;

2) для однородного шара радиуса R , массой m относительно оси, проходящей через его середину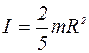

3) для тонкого однородного кольца (обруча) радиуса R массой m относительно оси, проходящей через центр перпендикулярно к плоскости кольца J = mR2 и т.д.

Для тел геометрически неправильной формы массы m момент инерции определяется экспериментальным путем.

Основное уравнение динамики вращательного движения тела можно записать в ином виде, учитывая, что 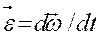, 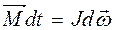или

(5)

Величина 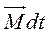называется импульсом момента сил, приложенных к телу, а d() - изменение момента количества движения тела (момента импульса тела).

Приведенное равенство (5) показывает, что изменение момента количества движения вращающегося тела равно импульсу момента приложенных к нему сил.

Если 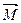=О, то d(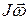)= 0 или , т.е. момент количества движения остается постоянным.

Это следствие называется законом сохранения момента количества движения: если сумма моментов сил 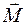, действующих на тело, равна нулю (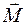= 0), то момент импульса тела 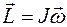остается постоянным (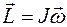= const). Например, при выполнении «сальто» в прыжке человек «группируется», прижимая голову и ноги друг к другу, тем самым снижает момент инерции J своего тела; а так как 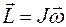= const, то угловая скорость вращения тела 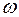повышается и, следовательно, время переворота человека уменьшается.

Изучение законов вращательного движения в лабораторной работе производится с помощью маятника Обербека, который представляет собой крестовину, состоящую из 4-х стержней каждый длиной l/2, прикрепленных к втулке с осью (рис.4).

На стержнях фиксируются грузы массой m1, которые могут быть закреплены симметрично на различных расстояниях от оси вращения. На шкив радиусом r, находящийся на оси вращения, наматывается нить, к свободному концу которой прикрепляется груз Р.

Если предоставить грузу Р возможность двигаться, то это падение будет происходить с ускорением а. При этом шкив со стержнями и расположенными на них грузами будет вращаться с угловым ускорением e, которое можно найти, измерив высоту h и время падения груза t.

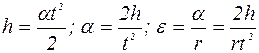(6)

где r - радиус шкива, на который наматывается нить.

Силой, создающей вращающий момент, является сила натяжения нити Т. Из второго закона Ньютона для груза Р следует 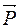+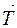=m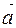. Переходя от векторной суммы к алгебраической, проектируя на ось ОХ имеем: Р - Т = ma, откуда

 

T = P - ma = mg - ma = m(g-a) (7)

Тогда вращающий момент

M = Tr = m(g-a)r (8)

Момент инерции маятника может быть определен из основного уравнения вращательного движения:

J=M/e (9)

Подставляя в формулу (9) формулы (5) и (7) получим окончательное выражение для момента инерции маятника Обербека, определенного практически (экспериментально):

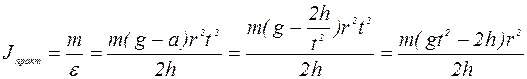. (10)

 

С другой стороны, теоретически, момент инерции маятника может быть найден из формулы Jтеорет 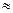Jk + 4Jrp (моментом инерции цилиндра радиуса r пренебрегаем), где Jk - момент инерции крестовины, Jrр - момент инерции груза относительно оси вращения. Считая груз материальной точкой массой m1, его момент инерции можно найти по формуле Jrp= m1R2, где R - расстояние от оси вращения до центра масс груза.

Тогда момент инерции крестовины теоретически определяется по формуле:

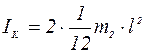
где m2 - масса «двойного» стержня, l – его длина (см. рис.4). (11)