Мета роботи
Навчитись моделювати процес руху однорідної нафти по трубопроводах, визначати основні параметри потоку та фактори, які на нього впливають.
3.2 Теоретичні відомості
Рух рідини по трубах часто спостерігаємо в техніці й у побуті. По трубах водопроводу вода надходить у будинки, до місць її споживання. У машинах по трубах надходить масло для змащування, пальне — в двигуни тощо.
Як відомо, нерухома рідина в посудині, згідно із законом Паскаля передає зовнішній тиск в усі точки рідини без зміни. Проте, коли рідина тече без тертя по трубі, площа поперечного перерізу якої на різних ділянках неоднакова, то, як показує дослід, тиск буде різним уздовж труби. З’ясуємо, чому тиск у рухомій рідині залежить від площі поперечного перерізу труби. Але спочатку ознайомимося з однією важливою особливістю всякого потоку рідини.
Припустимо, що рідина тече по горизонтально розміщеній трубі, переріз якої в різних місцях неоднаковий, наприклад по трубі, частину якої зображено на рисунку 3.1.
Якби ми уявно провели вздовж труби кілька перерізів, площі яких відповідно дорівнюють S1, S2, S3, і виміряли об’єм рідини, що протікає через кожний з них за якийсь інтервал часу то виявили б, що через кожний переріз протікає однаковий об’єм рідини. Це означає, що вся та рідина, яка за час t проходить через перший переріз S1, за такий самий час проходить і через третій переріз S3, хоча він за площею значно менший за S1.

Рисунок 3.1 - Поперечний переріз складного трубопроводу
Якби це було не так і через переріз площею S3 за час проходило, наприклад, менше рідини, ніж через переріз площею S1, то надлишок рідини повинен був би десь нагромаджуватись. Але рідина заповнює всю трубу і нагромаджуватись їй ніде. При цьому вважаємо, що задана маса рідини завжди має однаковий об’єм, що вона не може стиснутися і зменшити свій об’єм (про рідину говорять, що вона нестислива).
Як же може рідина, що протекла через широкий переріз, встигнути за такий самий час «протиснутися» через вузький? Очевидно, що для цього під час проходження вузьких частин труби швидкість руху має бути більшою, ніж під час проходження широких
Наприклад, добре відомо, що у вузьких місцях річки швидкість течії води більша, ніж у широких.
Оскільки при переході рідини з ділянки труби з більшою площею перерізу на ділянку з меншою площею перерізу швидкість течії зростає, то рідина рухається з прискоренням. А це за другим законом Ньютона означає, що на рідину діє сила. Цією силою може бути тільки різниця між силами тиску в широкій і вузькій ділянках труби. Отже, у широкій ділянці тиск рідини має бути більший, ніж у вузькій ділянці труби. Це саме випливає із закону збереження енергії.
Справді, якщо у вузьких місцях труби зростає швидкість руху рідини, то збільшується і її кінетична енергія. Та оскільки ми вважаємо, що рідина тече без тертя, то це збільшення кінетичної енергії має компенсуватися зменшенням потенціальної енергії, бо повна енергія повинна залишатися сталою. Про яку ж потенціальну енергію тут ідеться? Якщо труба горизонтальна, то потенціальна енергія взаємодії із Землею в усіх частинах труби однакова і не може змінитися. Отже, залишається тільки потенціальна енергія пружної взаємодії. Сила тиску, яка змушує рідину текти по трубі,— це є сила пружності стисненої рідини. Коли ми говоримо, що рідина нестислива, то маємо на увазі, що вона не може бути стиснена настільки, щоб помітно змінився її об’єм, проте дуже мале стискання, що спричиняє виникнення сил пружності, обов’язково відбувається. Ці сили й створюють тиск рідини. Саме це стискання рідини й зменшується у вузьких частинах труби. Тому у вузьких місцях труб тиск рідини повинен бути менший, ніж у широких.
У цьому полягає закон, що його відкрив академік Даниїл Бернуллі: тиск рухомої рідини більший у тих перерізах труби, в яких швидкість її руху менша, і, навпаки, у тих перерізах, у яких швидкість більша, тиск менший.
Наведені міркування стосуються випадку, коли рідину в трубі можна розглядати як замкнену систему. Адже тільки для такої системи справджується закон збереження енергії. У реальних випадках рідина тече в трубі під дією зовнішньої сили, яка створює різницю тисків. При цьому енергія змінюється і її зміна, дорівнює роботі зовнішньої сили. Проте закон Бернуллі залишається справедливим і в цьому випадку.
Чим менша площа перерізу труби, тим більша в ній швидкість течії і менший тиск. Очевидно, можна підібрати такий переріз, у якому тиск дорівнює зовнішньому атмосферному тиску. А якщо взяти ще менший переріз, то тиск рідини в ньому буде менший від атмосферного.
3.3 Порядок проведення розрахунків
Розрахунки проводимо за наступною схемою:
- задаємося внутрішнім діаметром труби di [м], витратою нафти Q[м3/c];
визначаємо швидкість руху рідини у трубопроводі:
 . (3.1)
. (3.1)
- визначаємо число Рейнольдса
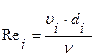 . (3.2)
. (3.2)
де 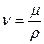 - коефіцієнт кінематичної в’язкості нафти, [м2/с];
- коефіцієнт кінематичної в’язкості нафти, [м2/с];  - коефіцієнт динамічної в’язкості нафти, , [Па∙с];
- коефіцієнт динамічної в’язкості нафти, , [Па∙с];  - густина нафти, [кг/м3].
- густина нафти, [кг/м3].
- визначаємо коефіцієнт гідравлічного опору труб:
ламінарний режим руху:
 ,
,  ; (3.3)
; (3.3)
турбулентний режим руху (зона гідравлічно-гладких труб):
 ,
, 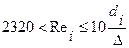 ; (3.4)
; (3.4)
зона змішаного опору:

 ; (3.5)
; (3.5)
зона квадратичного опору:
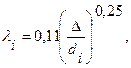
 . (3.6)
. (3.6)
де  - еквівалентна шорсткість труб.
- еквівалентна шорсткість труб.
- обчислюємо втрати тиску на тертя:
 . (3.7)
. (3.7)
де L – довжина трубопроводу, м;
- будуємо графічні залежності:

3.4 Варіанти завдань:
Густина нафти 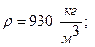
Коефіцієнт динамічної в'язкості нафти 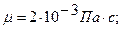
Довжина трубопроводу 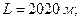
Коефіцієнт шорсткості матеріалу труб 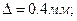
Внутрішній діаметр трубопроводу 
Витрата рідини 
3.5 Контрольні запитання
3.5.1. Як змінюється швидкість руху рідини і тиск при зміні перерізу трубопроводу?
3.5.2. Чому тиск в кінці трубопроводу і на початку не однаковий? Чим це пояснюється?
3.5.3. Наведіть і поясніть залежність для визначення числа Рейнольдса при русі рідини.
3.5.4. За якою залежністю розраховуються втрати тиску на тертя?
3.5.5. Охарактеризуйте режими руху рідини.