Lt; о) < а] .

По сути, дисперсия оценок зависимой переменной У— это та часть ее пол­ной дисперсии, которая обусловлена влиянием независимой переменной X.

Неизвестную дисперсию оценок У можно выразить через другие, извест­ные статистики, зная рассмотренные ранее свойства дисперсии:

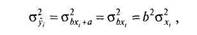
так как прибавление константы а к каждому значению переменной не меняет дисперсию, а умножение на константу b — увеличивает дисперсию в />²раз. Подставляя в формулу выражение для b из (6.2) получаем:

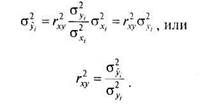
(6.4)

Иначе говоря, отношение дисперсии оценок зависимой переменной к ее ис­тинной дисперсии равно квадрату коэффициента корреляции.

Выражение (6.4) дает еще один вариант интерпретации корреляции. Квад­рат коэффициента корреляции (R Square) зависимой и независимой перемен­ных представляет долю дисперсии зависимой переменной, обусловленной влиянием независимой переменной, и называется коэффициентом детерми­нации. Коэффициент детерминации г_ху, таким образом, показывает, в какой сте­пени изменчивость одной переменной обусловлена (детерминирована) вли­янием другой переменной.

ГЛАВА 6. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ

ПРИМЕР______________________________________________________________

В большинстве исследований взаимосвязи IQ и успеваемости в школе корреляции этих показателей не превышают 0,5—0,7, т. е. коэффициент детерминации достигает величин 0,25—0,49. Иными словами, индивидуальная изменчивость (дисперсия) сред­него балла успеваемости может быть предсказана по результатам тестирования IQ не более чем на 25—49%. Означает ли это, что успешность обучения не более чем на 25—49% зависит от интеллекта? Ответ зависит от того, в какой мере средний балл отметок отражает успешность обучения, а тест IQ — интеллектуальные способности учащегося. Во всяком случае, этот пример демонстрирует явно не высокую эффек­тивность двумерной регрессии в деле практического предсказания¹.

Коэффициент детерминации обладает важным преимуществом по сравне­нию с коэффициентом корреляции. Корреляция не является линейной функци­ей связи между двумя переменными. Поэтому, в частности, среднее арифмети­ческое коэффициентов корреляции для нескольких выборок не совпадает с корреляцией, вычисленной сразу для всех испытуемых из этих выборок (т. е. коэффициент корреляции не аддитивен). Напротив, коэффициент детерми­нации отражает связь линейно и поэтому является аддитивным: допускается его усреднение для нескольких выборок.

Дополнительную информацию о силе связи дает значение коэффициента корреляции в квадрате — коэффициент детерминации г²: это часть диспер­сии одной переменной, которая может быть объяснена влиянием другой пе­ременной. В отличие от коэффициента корреляции г² линейно возрастает с увеличением силы связи. На этом основании можно ввести три градации ве­личин корреляции по силе связи:

г < 0,3 — слабая связь (менее 10% от общей доли дисперсии);

0,3 < г < 0,7 — умеренная связь (от 10 до 50% от общей доли дисперсии);

г > 0,7 — сильная связь (50% и более от общей доли дисперсии).

ЧАСТНАЯ КОРРЕЛЯЦИЯ

Очень часто две переменные коррелируют друг с другом только за счет того, что обе они согласованно меняются под влиянием некоторой третьей пере­менной. Иными словами, на самом деле связь между соответствующими свой­ствами отсутствует, но проявляется в статистической взаимосвязи (корреля­ции) под влиянием общей причины.

ПРИМЕР______________________________________________________

Общей причиной изменчивости двух переменных («третьей переменной») может яв­ляться возраст при изучении взаимосвязи различных психологических особеннос­тей в группе детей разного возраста. Предположим, что изучается взаимосвязь меж­ду зрелостью моральных суждений — Хп скоростью чтения — К Но в распоряжении

¹ С более совершенными методами предсказания книга знакомит вас в части 3: «Много­мерные методы...»

ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ

исследователя имеется лишь выборка из 45 детей разного возраста — от 8 до 14 лет (переменная Z— возраст). Если будет получена существенная положительная корре­ляция между Хи Y, например г_ху = 0,54, то о чем это будет свидетельствовать? Осто­рожный исследователь вряд ли сделает однозначный вывод о том, что зрелость мо­ральных суждений непосредственно связана со скоростью чтения. Скорее всего, дело втом, что и зрелость моральных суждений, и скорость чтения повышаются с возрас­том. Иными словами, возраст является причиной согласованной (прямо пропорци­ональной) изменчивости и зрелости моральных суждений, и скорости чтения.

Для численного определения степени взаимосвязи двух переменных при усло­вии исключения влияния третьей применяют коэффициент частной корреляции{Partial Correlation). Для вычисления частной корреляции достаточно знать три коэффициента корреляции г-Пирсона между переменными X, Yu Zfr^, r_xz и r_yz):

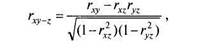
(6.5)

где r_xy^_z — частная корреляция Хи Упри постоянном Z(kiih с учетом Z).

Частная корреляция r_xy__z равна г_ху при любом фиксированном значении Z (в том случае, если Zлинeйнo коррелирует с Хтл У). Например, если значение частной корреляции скорости чтения Хи зрелости моральных суждений К с учетом возраста ZpaBHO 0,2 {r_xy___z = 0,2) и возраст линейно коррелирует и с Хи с У, то с любой группе детей одного и того же возраста г_ху будет тоже равно 0,2.

ПРИМЕР 6.3

Один исследователь решил сопоставить антропометрические и психологические данные исследования довольно большой группы детей. Каково же было его изум­ление, когда обнаружилась существенная положительная корреляция между скоро­стью решения арифметических задач и размером стопы: г_ху = 0,42. Оказалось, однако, что дети были разного возраста. Корреляция размера стопы с возрастом составила r_xy = QJ, а корреляция скорос­ти решения арифметических задач с возрастом г_у, = 0,6. Эти данные позволяют выяснить, взаимосвязаны ли размер стопы и скорость решения арифметических задач с учетом возраста (при условии, что возраст остается неизменным). Для этого необходимо вычислить частный коэффициент корреляции между размером стопы Хи скоростью решения арифметических задач К(при фиксированном возрасте Z):

0,42-0,7-0,6

^rxy-z ⁼ I ⁼ "

V(l-0,7²)(l-0,6²)

Таким образом, размер стопы и скорость решения арифметических задач корре­лируют исключительно за счет согласованности возрастной изменчивости этих показателей: частная корреляция между ними (с учетом возраста) равна нулю. И ес­ли мы возьмем группу детей одного и того же возраста, то корреляция размера сто­пы и скорости решения арифметических задач будет равна нулю.

ГЛАВА 6. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ

Следует быть особенно осторожным, пытаясь дать интерпретацию част­ной корреляции с позиций причинности. Например, если Zкоррелирует и с 1и с Y, а частная корреляция r_xy__z близка к нулю, из этого не обязательно следует, что именно Zявляeтcя общей причиной для Хн Y.

РАНГОВЫЕ КОРРЕЛЯЦИИ

Если обе переменные, между которыми изучается связь, представлены в порядковой шкале, или одна из них — в порядковой, а другая — в метричес­кой, то применяются ранговые коэффициенты корреляции: r-Спирмена или т-Кенделла. И тот, и другой коэффициент требует для своего применения предварительного ранжирования обеих переменных.

Коэффициент корреляции г-Спирмена

Если члены группы численностью /Убыли ранжированы сначала по пере­менной X, затем — по переменной Y, то корреляцию между переменными Хм Кможно получить, просто вычислив коэффициент r-Пирсона для двух рядов рангов. При условии отсутствия связей в рангах (т. е. отсутствия повторяю­щихся рангов) по той и другой переменной, формула для r-Пирсона может быть существенно упрощена в вычислительном отношении и преобразована в формулу, известную как г-Спирмена:

(6.6)

где с/, — разность рангов для испытуемого с номером /.

Коэффициент корреляции r-Спирмена (Spearman's rho) равен коэффициен­ту корреляции /--Пирсона, вычисленному для двух предварительно ранжиро­ванных переменных.

ПРИМЕР 6.4___________________________________________________________

Предположим, для каждого из 12 учащихся одного класса известно время решения тестовой арифметической задачи в секундах (X) и средний балл отметок по мате­матике за последнюю четверть (Y).

 

№	X	Y	Ранги X	Ранги Y	d,	d]
		4,7		2
		4,5
		4,4
		3,8			-4

ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ

 

№	X	Y	Ранги X	Ранги У	d,	d]
		3,7			_4
		4,6
		4,0			-5
		4,2			-5
		4,1
		3,6			_7
		3,5			-10
		4,8
S	-	-

Для расчета корреляции г-Спирмена сначала необходимо ранжировать учащихся по той и другой переменной. После ранжирования можно проверить его правиль­ность: сумма рангов должна быть равна N(N+ l)/2. Затем для каждого испытуемо­го надо вычислить разность рангов (сумма разностей рангов должна быть равна 0). После этого для каждого испытуемого вычисляется квадрат разности рангов — ре­зультат приведен в последнем столбце таблицы. Сумма квадратов разностей рангов равна 474. Подставляем известные значения в формулу 6.6:

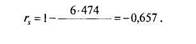
12(144-1)

Получена умеренная отрицательная связь между успеваемостью по математике и временем решения арифметической задачи.

Отметим: то же значение корреляции было бы получено при использовании фор­мулы r-Пирсона непосредственно к рангам Хи Y. Применяя же формулу г-Пирсо-на к исходным значениям Хи Y, мы получим г_ху = —0,692.

Коэффициент корреляции т-Кендалла

Альтернативу корреляции Спирмена для рангов представляет корреляция т-Кендалла. В основе корреляции, предложенной М. Кендаллом, лежит идея о том, что о направлении связи можно судить, попарно сравнивая между со­бой испытуемых: если у пары испытуемых изменение по Xсовпадает по на­правлению с изменением по У, то это свидетельствует о положительной свя­зи, если не совпадает — то об отрицательной связи.

В примере 6.3 данные испытуемых 1 и 2 свидетельствуют об отрицательной связи — мы видим инверсию: по переменной Ху второго испытуемого ранг больше, а по переменной У— меньше. Данные испытуемых 2 и 3, напротив, демонстрируют со­впадение направления изменения переменных.

Корреляция т-Кендаллаесть разность относительных частот совпадений и инверсий при переборе всех пар испытуемых в выборке:

x = P(p)-P(q),

ГЛАВА 6. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ

где Р(р) и P(q) — относительные частоты, соответственно, совпадений и ин­версий. Всего в выборке численностью УУ существует N(N— l)/2 всех возмож­ных пар испытуемых. Следовательно,

P-Q

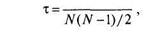
(6.7)

где Р — число совпадений, Q — число инверсий, а (Р+ Q) = N(N— l)/2. Формулу 6.7 можно представить и в ином виде:

т = ^-^- = 1---- I^_ = _Zi----- 1. (6,8)

P + Q N(N-l) N(N-l)

При подсчете т-Кендалла «вручную» данные сначала упорядочиваются по переменной X. Затем для каждого испытуемого подсчитывается, сколько раз его ранг по доказывается меньше, чем ранг испытуемых, находящихся ниже. Результат записывается в столбец «Совпадения». Сумма всех значений столб­ца «Совпадения» и есть Р — общее число совпадений, подставляется в фор­мулу 6.8. для вычисления т-Кендалла.

ПРИМЕР 6.5___________________________________________________________

Вычислим т-Кендалла для данных из примера 6.4. Сначала предварительно упоря­дочиваем испытуемых по переменной X. Затем подсчитываем число совпадений и инверсий для каждого испытуемого, сравнивая по Y его ранг с рангами испытуе­мых, находящихся под ним. Так, для первого испытуемого ранг по Кравен6,и 6 ис­пытуемых, находящихся ниже него, имеют по Y более высокий ранг: в столбец «Совпадения» записываем 6. Для третьего по счету испытуемого ранг по Y равен 8, трое испытуемых ниже него имеют более высокий ранг, значит, в столбец «Совпа­дения» записываем 3, и т. д.

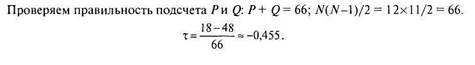
№	Ранги X	Ранги Y	Совпадения	Инверсии
			Р= 18	0 = 48

ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ

Для более полной интерпретации полезны соотношения между величи­ной х-Кендалла и вероятностью отдельно совпадений и инверсий:

 

Так, т = 0,5 значит, что вероятность совпадений равна 0,75, а вероятность инвер­сий — 0,25, то есть при сравнении объектов друг с другом прямо пропорциональ­ное соотношение (например, роста и веса) встречается в 3 раза чаще, чем обратно пропорциональное соотношение. Такая интерпретация кажется более понятной, чем, например, интерпретация корреляции Пирсона г= 0,5: «25% изменчивости в весе могут быть объяснены различиями в росте».

т-Кендалла кажется более простым в вычислительном отношении. Одна­ко при возрастании численности выборки, в отличие от л-Спирмена, объем вычислений х-Кендалла возрастает не пропорционально, а в геометрической прогрессии. Так, при N=12 необходимо перебрать 66 пар испытуемых, а при N = 48 — уже 1128 пар, т. е. объем вычислений вбзрастает более, чем в 17 раз.

Отметим важную особенность ранговых коэффициентов корреляции. Для метрической корреляции r-Пирсона значениям +1 или —1 соответствует пря­мая или обратная пропорция между переменными, что графически представ­ляет собой прямую линию. Максимальным по модулю ранговым корреляци­ям (+1, —1) вовсе не обязательно соответствуют строгие прямо или обратно пропорциональные связи между исходными переменными Хи Y: достаточна лишь монотонная функциональная связь между ними. Иными словами, ран­говые корреляции достигают своего максимального по модулю значения, если большему значению одной переменной всегда соответствует большее значе­ние другой переменной (+1) или большему значению одной переменной все­гда соответствует меньшее значение другой переменной и наоборот (—1).

Проблема связанных (одинаковых) рангов

В измерениях часто встречаются одинаковые значения. При их ранжиро­вании возникает проблема связанных рангов (Tied Ranks). В этом случае дей­ствует особое правило ранжирования: объектам с одинаковыми значениями

приписывается один и тот же, сред­ний ранг. Например, когда эксперт не может установить различие меж­ду двумя лучшими образцами това­ра, им приписывается одинаковый ранг: (1 + 2)/2 = 1,5. Это сохраняет неизменной сумму рангов для вы­борки объемом N: N(N + l)/2.

При наличии одинаковых (связан­ных) рангов формулы ранговой корре-

ГЛАВА 6. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ

ляции Спирмена (6.6) и Кендама (6.7и 6.8) не подходят. Хотя сумма рангов и не меняется, но изменчивость данных становится меньше. Соответственно, умень­шается возможность оценить степень связи между измеренными свойствами. При использовании корреляции Спирмена в случае связанных рангов возмож­ны два подхода:

□ если связей немного (менее 10% для каждой переменной), то вычис­
лить r-Спирмена приближенно по формуле 6.6;

□ при большем количестве связей применить к ранжированным данным
классическую формулу /"-Пирсона 6.1 — это всегда позволит опреде­
лить ранговую корреляцию независимо от наличия связей в рангах.

При использовании корреляции х-Кендалла в случае наличия связанных ран­гов в формулу вносятся поправки, и тогда получается общая формула для вы­числения т. коэффициента корреляции х_ь-Кендалла (Kendall's tau-b) независи­мо от наличия или отсутствия связей в рангах:

P-Q

'-l)/2]-K_xyj[N(N-l)/2]-K_y ' ⁽⁶'⁹⁾

где х = (1/2)У/■(/■-1) (' — количество групп связей по X,f_t — численность каждой группы); х = (1/2)У/(/)-1) (/ — количество групп связей по У,/ — численность каждой группы).

ПРИМЕР 6.6______________________________________________________________________

Супруги X и Y ранжировали 8 жизненных ценностей по степени предпочтения. Данные представлены в таблице:

 

Ценности	Ранги X	Ранги Y	Р (совпадения)	Q(инверсии)
Здоровье
Любовь
Богатство
Свобода
Мудрость
Познание
Развитие
Творчество
			2 = 20

В качестве меры согласованности предпочтений супругов вычислим корреляцию т₄-Кендалла, так как наблюдаются связи в рангах: одна группа из трех рангов по Хи две группы по три ранга по Y.

Обратите внимание на подсчет совпадений для объектов, попадающих в «связки». Например, для объекта «Богатство» пропускаются два ниже находящихся объекта, как имеющие одинаковые с ним ранги по X.

КОРРЕЛЯЦИЯ БИНАРНЫХ ДАННЫХ

Как отмечалось ранее, если одна из двух переменных представлена в но­минативной шкале, а другая — в числовой (ранговой или метрической), то связь между этими переменными лучше изучать путем сравнения групп по уровню выраженности числовой переменной.

ПРИМЕР _________________________________________________

Предположим, исследуется связь количества пропущенных лекций студентами и курса обучения (с 1-го по 5-й). Первая переменная — метрическая, а вторая — но­минативная. Связь между этими переменными может быть изучена путем сравне­ния разных курсов по количеству пропущенных лекций (по средним значениям). Если будут обнаружены различия между курсами, то посещаемость лекций связана с курсом обучения, в противном случае — связи нет.

То же касается проблемы изучения связи между двумя номинативными переменными. Хотя и для этого случая существуют коэффициенты корреля­ции (К— Чупрова, С — Пирсона), но возможность их интерпретации весьма ограничена, в частности потому, что они отражают лишь силу связи, но не ее направление. Поэтому и в этом случае проблему связи между двумя номина­тивными переменными лучше изучать путем сравнения градаций одной пе­ременной по распределению другой переменной.

ПРИМЕР

Предположим, исследуется связь агрессивности учащихся (три градации: низкая, средняя, высокая) и образования их родителей (среднее, высшее техническое, выс­шее гуманитарное). Результаты исследования связей двух номинативных перемен­ных обычно представляются в виде таблицы сопряженности:

 

 

Агрессивность	Образование родителей
Среднее	Высш. технич.	Высш. гуманит.
Низкая
Средняя
Высокая

ГЛАВА 6. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ

Связь между этими переменными может быть изучена путем сравнения распреде­лений учащихся по степени агрессивности для разных градаций образования роди­телей (или, что то же самое, путем сравнения распределения образования родите­лей для разных градаций степени агрессивности учащихся).

Исключением можно считать случай изучения связи двух бинарных перемен­ных. Бинарная переменная имеет только две градации, обычно обозначаемые как О и 1. Примеры таких переменных: пол (мужской, женский), образование (сред­нее, высшее), тревожность (низкая, высокая), успешность (низкая, высокая) и т. д. При изучении связей между бинарными переменными обычно строят че-тырехклеточные таблицы сопряженности:

Таблица 6.1 Таблица сопряженности 2x2

 

 

 

	Признак X	Итог
Признак Y		а	Ъ	а+ b
	с	d	с + d
Итог		а + с	b + d	N

Вэтом случае допустимо применение г-Пирсона (формула 6.1) непосред­ственно к исходным данным — двум бинарным переменным, принимающим значение 0 или 1, измеренным для каждого члена выборки численностью Л'. Результат применения r-Пирсона к двум бинарным переменным называется «фи-коэффициентом сопряженности» (Phi). Если данные представлены в четырех-клеточной таблице сопряженности, то применяется формула, существенно упрощающая расчеты, но дающая аналогичный результат:

ad-bc _c

ср = ■ , (6.10)

J(a + b)(c + d)(a + c)(b + d) где а, Ь, с, d соответствуют обозначениям в четырехклеточной таблице 6.1.

ПРИМЕР 6.7___________________________________________________________

Исследовалась связь семейного положения студенток (X: 0 — холостая, 1 — заму­жем) и их академической успеваемости (Y: 0 — закончила вуз, 1 — отчислена). В рас­поряжении исследователя есть данные для 12 студенток:

 

№

X

Y

Таблица сопряженности для этих данных:

 

 

 

	X	Итог
Y
Итог

ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ

Вычислим ф-коэффициент сопряженности:

 

Получена умеренная положительная взаимосвязь: холостые студентки чаше закан­чивают вуз, а замужние — чаще отчисляются. Отметим, что тот же самый результат был бы получен при применении формулы /'-Пирсона непосредственно к исход­ным данным.

Итак, ф-коэффициент есть просто /"-Пирсона, вычисленный для бинар­ных данных, а формула 6.10 алгебраически эквивалентна формуле 6.1. Следо­вательно, интерпретация ф-коэффициента подобна интерпретации /--Пирсо­на. Но использование ф-коэффициента существенно ограничено. Чем больше асимметрия распределения 0 и 1 по каждой переменной, тем менее точно ф-коэффициент отражает связь между бинарными переменными. Иначе го­воря, применение q-коэффициента требует приблизительного равенства коли­чества 0 и 1 по каждой переменной.

ВЕЛИЧИНА КОРРЕЛЯЦИИ И СИЛА СВЯЗИ

Коэффициенты корреляции были специально разработаны для численно­го определения силы и направления связи между двумя свойствами, измерен­ными в числовых шкалах (метрических или ранговых). Как уже упоминалось, максимальной силе связи соответствуют значения корреляции +1 (строгая прямая или прямо пропорциональная связь) и —1 (строгая обратная или об­ратно пропорциональная связь), отсутствию связи соответствует корреляция, равная нулю. Дополнительную информацию о силе связи дает значение ко­эффициента детерминации г²: это часть дисперсии одной переменной, кото­рая может быть объяснена влиянием другой переменной.

Однако в ряде случаев разные коэффициенты корреляции имеют различную эффективность, а иногда все они оказываются нечувствительными к связям.

Выбросы и отклонения распределений от нормальности

Выбросы— это экстремально большие или малые значения признака. В наибо­лее существенной степени выбросы вли­яют на корреляцию г-Пирсона, так как величина этого коэффициента прямо пропорциональна отклонению значения переменной от среднего.

ГЛАВА 6. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ

ПРИМЕР 6.8

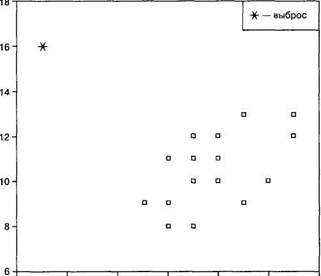
Воспользуемся данными из примера 6.1 с показателями вербального и невербаль­ного интеллекта, измеренного у 20 учащихся 8-го класса (г- 0,517). Добавим еще одно наблюдение: x₂₁ = 3,y₂i = 16 (см. рис. 6.5). Новое значение г-Пирсона для всех N= 21 теперь будет равно г— —0,124.

о.