Истинная скорость Vист - это скорость волны в малом объеме породы. Она определяется путем ультразвуковых измерений на образцах

Типы скоростей в слоистых средах.

В связи с разным строением слоистых сейсмических сред и границ в сейсморазведке используются следующие скорости (или типы скоростей) распространения упругих волн (V_p).

1. Истинная скорость V_ист - это скорость волны в малом объеме породы. Она определяется путем ультразвуковых измерений на образцах.

2. Пластовая скорость V_п - это средняя скорость распространения упругих волн в каждом пласте изучаемого геологического разреза.

3. Интервальная скорость V_инт является частным случаем средней скорости для заданного интервала глубин.

4. Средняя скорость V_ср в пачке пластов - это скорость, определяемая по формуле V_ср = (h₁+h₂+...+h_n)/(t₁+t₂+...+t_n), где h₁,h₂, ... h_n - мощности отдельных пластов данной слоистой среды; t₁,t₂,... t_n - времена пробега в каждом пласте, измеренные вдоль луча, перпендикулярного слоистости.

5. Эффективная скорость V_эф - это некоторая средняя скорость, определяемая в результате интерпретации данных сейсморазведки методом отраженных волн в предположении, что скорость в толще, покрывающей отраженную границу, постоянна.

6. Граничная скорость V_г - это скорость распространения скользящей преломленной волны вдоль преломляющей границы. Она рассчитывается при интерпретации данных сейсморазведки методом преломленных волн.

7. Кажущаяся скорость V_к - это скорость распространения фронта любой волны вдоль профиля наблюдений. В любой точке профиля наблюдений она равна отношению приращения пути Δx ко времени его прохождения волной Δt, т.е. V_к = Δx /Δt.

Пластовая, средняя и интервальная скорости определяются по сейсмическим наблюдениям в скважинах.

 

Решения прямых задач сейсморазведки

Прямой задачей сейсморазведки называется расчет времен прихода (t) для той или иной волны для известного сейсмогеологического разреза (кинематические задачи), когда известны: мощности, глубины залегания, размеры тех или иных геологических объектов (чаще слоев) и скорости распределения упругих волн, а также место источника. Традиционно простейшим результатом решения прямой задачи является получение уравнения годографа, или аналитического выражения для t(x) с дальнейшим построением годографа - графика зависимости времени прихода той или иной волны (t) от расстояния от пункта возбуждения до пункта приема (x).

 

Годограф прямой волны

Самой простой прямой задачей сейсморазведки является получение годографа прямой волны. Очевидно, что время прихода прямой волны после создания упругого импульса в пункте возбуждения или взрыва (ПВ) равно t = x/V. Поэтому годограф имеет вид прямой линии. По наклону прямой линии можно определить скорость V = Δx/ΔV.

Прямая и обратная задача отраженной волны для двухслойной среды с наклонной границей раздела.

1. Прямая задача. Прямая задача сейсморазведки методом отраженных волн (МОВ) сводится к получению уравнения годографа над разрезом с извест­ными мощностями слоев и скоростями распространения волн. Простейшим является двухслойный разрез с однородным изотропным верхним слоем и скачком акустической жесткости на наклонной границе с подстилающим полупространством.

Пусть под однородной покрывающей средой со скоростью распростра­нения упругих волн V₁ расположена вторая среда со скоростью V₂, а угол разделяющей их плоской границы равен φ. Если на границе раздела сред выполняется условие σ₁V₁ ≠σ₂V₂, то образуется однократная отраженная волна с углом отражения равным углу падения α. Требуется найти уравнение годографа, т.е. установить теоретическую зависимость времени прихода волны t от расстояния x, скорости распространения волны в перекрывающем слоеV₁, глубины по нормали к отражающей границе и его угла наклона φ.

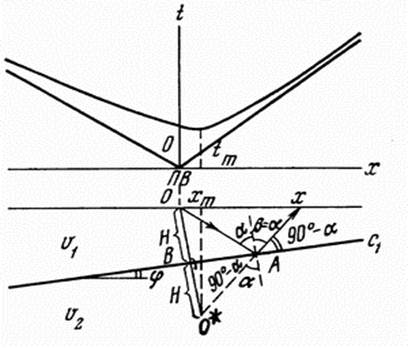Время прихода отра­же­нной волны в точку x профиля на­блю­дения равно t = (OA+Ax). Пусть О* - мнимый пункт взрыва, или точка, располо­же­нная на пер­пендикуляре к границе так, что OB = BO*. Oтрезки AO* и Ax лежат на одной линии и

. Из прямоугольного треугольника OO*x_m имеем Ox_m = 2Hsinφ и O*x_m = 2Hcosφ. Тогда

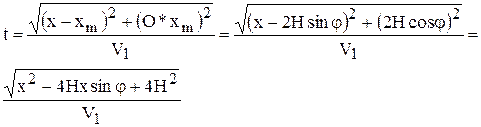
Это и есть уравнение линейного годографа однократно отраженной волны.

Полученное уравнение является уравнением гиперболы. Это гипербола, действительная ось которой параллельна оси t и смещена на 2Hsinφ по оси x.

Из уравнения годографа можно найти его характерные точки:

x₀ = 0; t₀ = 2H/V1; t_min = 2Hcosφ/V₁; x_min = 2Hsinφ.

При x > 4H годограф отраженной волны асимптотически приближается к годографу прямой волны. Если в уравнении годографа для точек профиля, расположенных от пункта возбуждения по восстанию пласта, при выражении 4Hsinφ стоит знак "минус", то для точек по падению пласта должен стоять знак "плюс".

2. Обратная задача. Обратная задача метода отраженных волн (МОВ) для модели наклонного контакта двух сред сводится к определению скорости в перекрывающем слое V₁ (в методе МОВ эту скорость для слоистой среды называют эффективной V_эф) и геометрических параметров разреза (H, φ). Обратная задача решается различными способами на основе анализа уравнения годографа. Рассмотрим простейшие из них.

А. Определение V_эф в перекрывающей толще по годографам отраженных волн способом постоянной разности при обработке одиночных годографов. Взяв две точки годографа, удаленные на расстояние m, запишем для них уравнения:

V₁²t₁² = x² + 4H² – 4Hxsinφ; V₁²t₂² = (x+m)² + 4H² – 4H(x+m)sinφ;

Вычтя из второго уравнения первое и обозначив U = t₂² – t₁², получим:

V₁²U = 2xm + m² – 4Hmsinφ. Продифференцировав это уравнение, получим dU = 2mdx/V₁². Учтя, что для прямой линии dU/dx = ΔU/Δx, легко получить формулу для расчета: V₁ = (2m ΔU/Δx)^0.5.

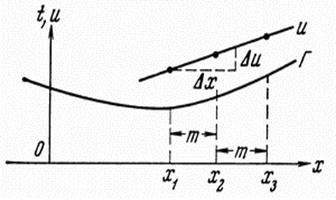При практическом применении полученной формулы поступают следующим образом. На годо­графе выбирается несколько пар точек (t₁ и t₂, t₂ и t₃), расположен­ных на постоянном расстоянии m друг от друга. Для каждой пары времен находится функция U = t₂² – t₁² и строится график функции U от x. Взяв приращение ΔU для какого-то Δx, легко рассчитать V₁.

Б. Способы построения отражающих границ. Получив V₁, можно определить глубину залегания отражающей границы и ее наклон, т.е. построить отражающую границу.

Наиболее простыми способами построений отражающей границы являются способ t₀ и способ засечек.

Способ t₀. Поскольку t₀ = 2H/V₁, где t₀ - время на пункте взрыва, которое можно определить по годографу (оно равно времени при x = 0), то глубина залегания равна H = t₀V₁/2.

Имея несколько ПВ (несколько годографов), можно построить отражающую границу как касательную к окружностям с радиусами H, проведенными из соответствующих ПВ.

Способ засечек. На профиле наблюдений выбирают 3 - 5 точек и из них

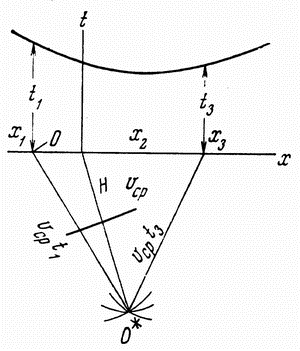проводят засечки радиусами R = V₁t. Засечки, пересекаясь примерно в одной точке, дают местоположение мнимого пункта взрыва O*, а отражающая граница располагается в середине и перпендикулярно OO*.

 

 

Прямая и обратная задача головной преломленной волны для двухслойной среды с плоской наклонной границей раздела.

1. Образование головной преломленной волны. При критическом угле паде­ния α = i, когда угол преломления β равен 90^о, вдоль границы начнет сколь­зить преломленная волна, которая возникает при V₂ > V₁, так как sin(i) = V₁/V₂ < 1.

При падении прямой сферической волны под критическим углом i в точке R образуются две волны: одна отраженная, движущаяся по лучу RS cо скоростью V₁, и вторая, скользящая вдоль границы раздела со скоростью V_г (V_г, как правило, равно V₂). Чтобы показать, как эта скользящая преломлен­ная волна выходит на линию наблюдений (ось х), воспользуемся принципом Гюйгенса.

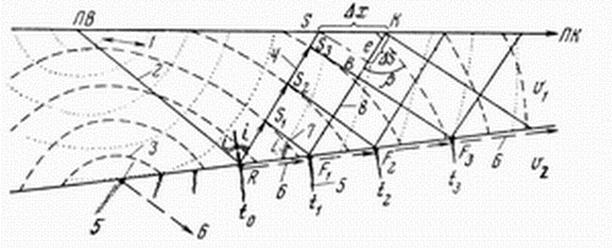
Природа образования сейсмических волн: 1, 2 - фронт и луч прямой волны; 3, 4 - фронт и луч отраженной волны; 5, 6 - фронт и луч преломленной проходящей волны; 7, 8 - фронт и луч головной преломленной волны

 

Согласно принципу Гюйгенса, любая точка фронта волны является источником колебаний. В частности, из точки R начнет распространяться фронт отраженной волны со скоростью V₁, который через время t₁ после начала отражения достигнет точки S₁. За это же время в среде V₂ фронт проходящей преломленной волны, перпендикулярный границе раздела, достигнет точки F₁. Соответственно за время t₂ фронты этих волн достигнут точек S₂ и F₂, за время t₃ – S₃ и F₃ и так далее. Поскольку V₂ > V₁, прелом­ленная волна распространяется быстрее отраженной.

Фронт проходящей преломленной волны, скользя вдоль границы разде­ла, возбуждает в верхнем слое колебания, которые и вызывают появление так называемой головной преломленной волны. В точке S, где возникает голов­ная волна, фронты отраженной и головной волн выйдут на поверхность одно­временно, а далее отраженная волна, поскольку она имеет меньшую ско­рость, начнет отставать от головной.

Фронты головной преломленной волны будут плоскостями, наклонен­ными под углом i к границе раздела, а лучи, перпендикулярные фронту, будут наклонены под постоянным углом е к поверхности наблюдений. Фронт головной волны будет скользить вдоль линии наблюдений с кажущейся скоростью V_k = Δx/Δt. Из треугольника SBK легко получить выражение для кажущейся скорости (закон кажущихся скоростей, закон Бенндорфа). В самом деле, ΔS = V₂Δt =Δxcos(e), отсюда V_k = V₁/cos(e), т.е. для данной среды V_k = const. Т.к. угол е равен i – φ (как углы со взаимноперпендикулярными сторонами), то V_k = V₁/sin(i±φ), где знак плюс взят по падению пласта, а знак минус - по восстанию пласта.

2. Уравнение годографа преломленной волны.

Пусть под однородной покрываю­щей средой со скоростью распро­странения упругих волн V1 рас­положена плоская граница второго слоя с V2 > V1. Требуется получить уравнение годографа головной пре­ло­мленной волны, т.е. установить зависимость времени прихода вол­ны (t) от расстояния (x), скорости распространения упругих волн (V1 и V2), глубины залегания (H) и угла нак­лона (φ) преломляющей границы.

Первой точкой профиля наблюдений, в которой начинает регистриро­ваться преломленная волна, является точка S (x_н, t_н), называемая начальной точкой головной волны. Так как все лучи головной преломленной волны параллельны, то углы е и V_k = Δx/Δt постоянны, а это значит, что линейный годограф преломленной волны имеет постоянный наклон к оси x. Наклон к оси х остается постоянным лишь у прямой линии. Таким образом, годограф головной преломленной волны над плоской границей является прямой лини­ей, начинающейся в точке S’ с координатами (x_н, t_н) и накло­ненной к оси x под углом tg(α) = Δt/Δx = 1/V_k.

Отсюда можно получить уравнение годографа преломленной волны. По восстанию пласта Δt/Δx = (t-t_н)/(x-x_н) = 1/V_kв, где t и x - координаты любой точки годографа. Очевидно, для получения уравнения необходимо опре­де­лить t_н и x_н.

Возьмем мнимый пункт взрыва O’ и опустим перпендикуляры на О'S и ось x. Из треугольника OKS x_н = OK / sin(e), из треугольника OO'K OK = 2Hsin(i). Учитывая, что e_в = 90^o – (i – φ), получим , . Из треугольников О'AS и OO'A можно получить O’S = O’A/cos(i - φ) и O’A = 2Hcos(φ). Откуда t_нв = 2Hcos(φ)/V₁cos(i – φ). Для точек по падению границы x_нп = 2Hsin(i)/cos( i+ φ), t_нп = 2Hcos(φ)/V₁cos(i + φ).

Учитывая, что V_кв = V₁/sin(i – φ), получаем уравнение годографа преломленной волны:

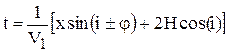
Знак "-" берется для годографа по восстанию границы (здесь волна приходит быстрее), знак "+" берется для годографа по падению границы от пункта взрыва. Из уравнений годографов видно, что при х = 0, t₀ = 2Hcos(i)/V₁, где t₀ - время на пункте взрыва.

Для горизонтальной преломляющей границы (φ = 0) t = [xsin(i)+2Hcos(i)]/V₁.

Выражение для годографа преломленной волны можно записать в таком виде: t = t₀ + xsin(i + φ)/V₁ = t₀ + x/V_k.

При φ >i V_кв <0, что означает приход волны сначала к удаленным, а затем к близким к пункту взрыва точкам наблюдения. При i + φ > 90^o, V_кп <0 и t_нп < 0, что соответствует случаю, когда головная преломленная волна не сможет выйти на поверхность и работы методом МПВ невозможны. Поэтому этот метод может применяться для изучения не очень крутых структур, т.е. при углах падения, меньших 45.

Преломленная волна на удалении x > x_н от пункта взрыва всегда приходит раньше отраженной и прямой волн и ее удобно регистрировать в области первых вступлений.

Годограф волны, преломленной на плоской границе двух сред, прямо­линеен. Однако, если преломляющая граница криволинейна, то и годограф приобретает криволинейную форму. Это объясняется тем, что угол выхода сейсмической радиации е = 90о – (i ± j ) и кажущаяся скорость Vk = V1/sin(i ± j ) меняется при изменении угла наклона границы (j) по профилю наблю­де­ний, что приводит к изменению угла наклона годографа.

3. Обратная задача метода преломленных волн. Обратная задача метода преломленных волн (МПВ) над наклонной границей двух сред сводится к определению скоростей в верхнем (V₁) и нижнем (V₂ = V_г) слоях и геометрических параметров разреза (Н, j, i). Ее решают различными способами, основанными на анализе уравнения годографа. Как показывает практика интерпретации МПВ, наиболее надежно решить обратную задачу можно, имея встречные годографы (Г1 и Г2), которые получаются из двух точек взрыва О1 и О2, находящихся на концах изучаемого профиля (рис. 4.8).

Определение граничной скорости с помощью разностного годографа и построение преломляющей границы способом t₀.

А. Определение граничной скорости по разностному годографу. Имея два встречных годографа, можно построить разностный годограф: Q(x) = t₁(x) –t₂(x) + T, где t₁(x) и t₂(x) - время прихода головной преломленной волны в точку х по первому и второму (встречному) годографу, T - время во взаимных точках, т.е. время прихода волны из О₁ в О₂ или из О₂ в О₁. Путь головной волны из пункта взрыва О₁ в точку О₂ и, наоборот, из пункта взрыва О₂ в точку О₁ одинаков, а значит, время во взаимных точках по встречным годографам одинаково и постоянно для данного интервала О₁О₂.

Взяв производную от уравнения разностного годографа, получим dQ/dx = dt₁/dt – dt₂/dx, где dQ/dx = DQ/Dx - угловой коэффициент разностного годографа, равный обратной скорости, т.е. dt₁/dx = Dt₁/Dx = 1/V_кв и dt₂/dx = Dt₂/Dx = 1/V_кп. Отсюда DQ/Dx = 1/V_кв + 1/V_кп = [sin(i+j) + sin(i-j)]/V₁ = 2cos(j)/V₁.

Таким образом, граничная скорость может быть определена по наклону разностного годографа V_г = 2cos(j)Dx/DQ. При углах наклона, меньших 10 – 15^o, V_г » 2Dx/DQ.

Б. Определение скорости в перекрывающем слое. Скорость упругих волн в перекрывающем слое (толще) может быть оценена по точкам пересечения годографов прямой и головных преломленных волн: V₁ » V_ср » x_тп/t_тп , где x_тп и t_тп - координаты точек пересечения.

Однако более точно V_ср » V_эф получается по данным метода отраженных волн.

В. Построение преломляющей границы способом нулевого времени. Одним из простых и точных способов определения H, j и построения преломляющей границы является способ нулевого времени (t₀).

Для любой точки S, где имеются два встречных годографа можно найти некоторую функцию t₀ = t₁ + t₂ - T, которая равна времени на пункте взрыва t₀ = 2Hcos(i)/V₁. Практически применение способа t₀ сводится к следующему. Для любой точки х определяется величина Dt = T – t₂. От значения t₁по первому годографу измерителем откладывается Dt вверх (получаем точку разностного годографа Q = t₁ + Dt = t₁ – t₂ +T) и вниз (получаем t₀ = t₁ - Dt = t₁ + t₂ - T). Сделав подобные построения в нескольких (3 - 5) точках оси х и соединив точки Q и t₀, получаем разностный годограф Q(x) и линию t₀(x). По наклону разностного годографа находится граничная скорость V_г » Dx/DQ (при j < 15^o). Если угол j > 15^o, то ее можно определить по формуле, приведенной выше (V_г = 2cos(j)Dx/DQ). Зная t₀ в каждой точке можно рассчитать эхо-глубину H.

Проведя из нескольких точек х дуги радиусами H и соединив их плавной касательной, получим искомую преломляющую криволинейную границу раздела. Для криволинейной границы не имеет смысла говорить об угле наклона j, поскольку он разный в разных точках преломляющей границы.

 

Обобщенный годограф

Для примера возьмем трехслойную среду с горизонтальными границами и с параметрами H₁ = 5м, V₁ = 500 м/сек (четвертичные отложения), Н₂ = 30 м, V₂ = 4000 м/сек (терригенные отложения татарского яруса) и V₃ = 6000 м/сек (карбонатные отложения казанского яруса).

Средняя скорость V_ср в пачке пластов - это скорость, определяемая по формуле V_ср = (h₁+h₂+...+h_n)/(t₁+t₂+...+t_n), где h₁,h₂, ... h_n - мощности отдельных пластов данной слоистой среды; t₁,t₂,... t_n - времена пробега в каждом пласте, измеренные вдоль луча, перпендикулярного слоистости

Для прямой волны: t = x/V;

Для отраженной волны: x₀ = 0; t₀ = 2H/V1;

Для преломленной волны: 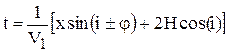, для горизонтальной границы (φ = 0) при х = 0, t₀ = 2Hcos(i)/V₁, где t₀ - время на пункте взрыва.

x_нп = 2Hsin(i)/cos( i) = 2Htg(i), t_нп = 2H/[V₁cos(i)], V_k = V1/sin(i ), наклон годографа преломленных волн к оси x = Δt/Δx = 1/V_k.

Для отраженной волны от первой границы t₀ = 2H/V1 = 2*5/500 = 0.02 c. Преломленная волна от первой границы : sin(i) = V₁/ V₂ = 0.13, cos(i) = 0.96, tg(i) = 0.14. x_нп = 10*0.14 = 1.4 м, t_нп = 2H/[V₁cos(i)] = 0,025 с, V_k = V₁/sin(i ) = 500/0.13 = 3800,

Δt/Δx = 1/V_k = 2,6*10-4, для 100 м будет 0,026 сек.

Средняя скорость для первых двух слоев равна V_ср = (5+30)/(5/500+30/4000) = 1750 м/с

Для отраженной волны от 2 границы t₀ = 2H/V_ср = (5+30)/1750 = 0.02 с

Преломленная волна от 2 границы :sin(i) = V_ср/ V₃ = 0.3, cos(i) = 0.95, tg(i) = 0.32; x_нп = 2*35*0.3 = 21 м, t_нп = 2H/[V₁cos(i)] = 2*35/(1750*0.95) =0,021 с, V_k = V₁/sin(i ) = 1750/0.3 = 5830, Δt/Δx = 1/V_k = 1,7*10-4, для 100 м будет 0,017 сек.